Menu Close

Question-81251

Tinku Tara 0 Comments
Pin




Question Number 81251 by mr W last updated on 10/Feb/20
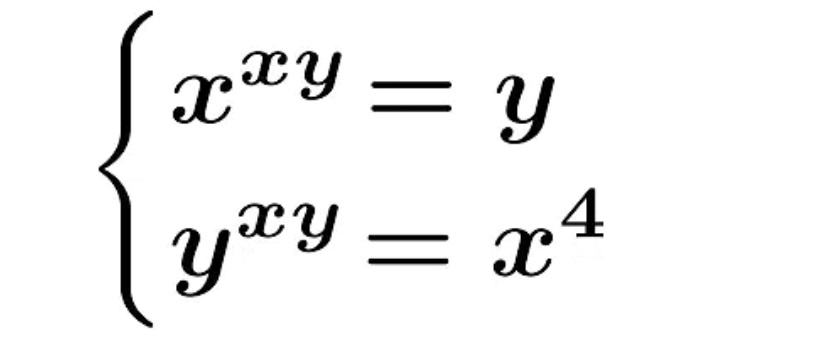
Commented by mind is power last updated on 10/Feb/20
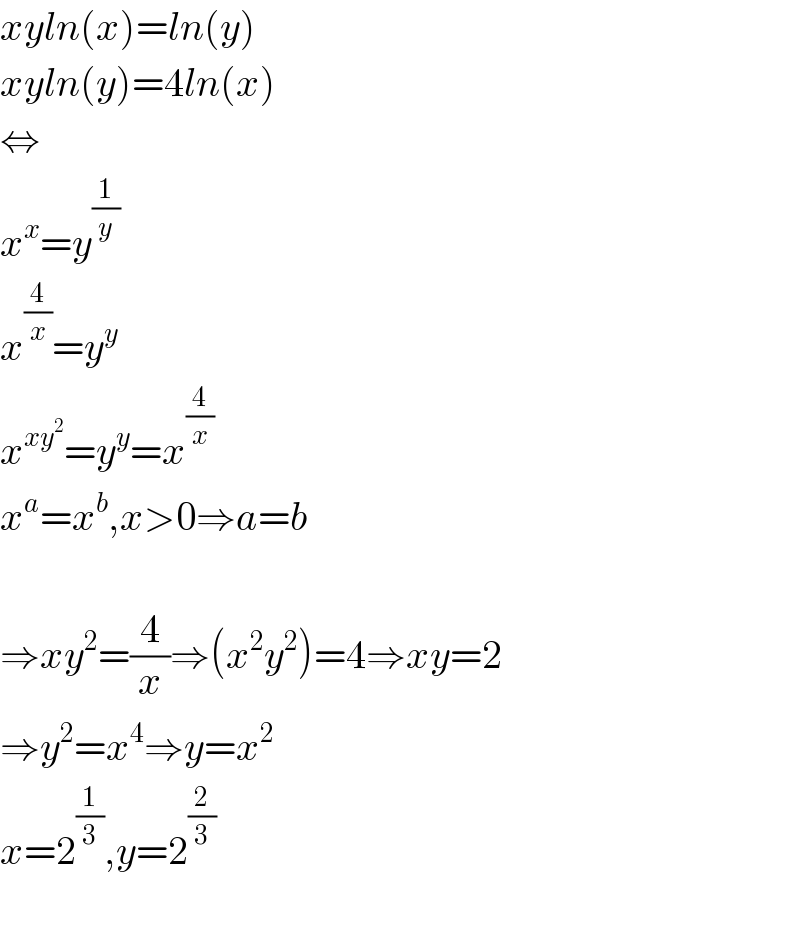
xyln(x)=ln(y) xyln(y)=4ln(x) ⇔ x^x =y^(1/y) x^(4/x) =y^y x^(xy^2 ) =y^y =x^(4/x) x^a =x^b ,x>0⇒a=b ⇒xy^2 =(4/x)⇒(x^2 y^2 )=4⇒xy=2 ⇒y^2 =x^4 ⇒y=x^2 x=2^(1/3) ,y=2^(2/3)
$${xyln}\left({x}\right)={ln}\left({y}\right) \\ $$$${xyln}\left({y}\right)=\mathrm{4}{ln}\left({x}\right) \\ $$$$\Leftrightarrow \\ $$$${x}^{{x}} ={y}^{\frac{\mathrm{1}}{{y}}} \\ $$$${x}^{\frac{\mathrm{4}}{{x}}} ={y}^{{y}} \\ $$$${x}^{{xy}^{\mathrm{2}} } ={y}^{{y}} ={x}^{\frac{\mathrm{4}}{{x}}} \\ $$$${x}^{{a}} ={x}^{{b}} ,{x}>\mathrm{0}\Rightarrow{a}={b} \\ $$$$ \\ $$$$\Rightarrow{xy}^{\mathrm{2}} =\frac{\mathrm{4}}{{x}}\Rightarrow\left({x}^{\mathrm{2}} {y}^{\mathrm{2}} \right)=\mathrm{4}\Rightarrow{xy}=\mathrm{2} \\ $$$$\Rightarrow{y}^{\mathrm{2}} ={x}^{\mathrm{4}} \Rightarrow{y}={x}^{\mathrm{2}} \\ $$$${x}=\mathrm{2}^{\frac{\mathrm{1}}{\mathrm{3}}} ,{y}=\mathrm{2}^{\frac{\mathrm{2}}{\mathrm{3}}} \\ $$$$ \\ $$
Commented by mr W last updated on 10/Feb/20
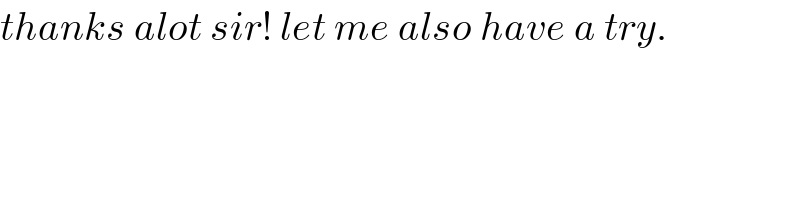
thanks alot sir! let me also have a try.
$${thanks}\:{alot}\:{sir}!\:{let}\:{me}\:{also}\:{have}\:{a}\:{try}. \\ $$
Commented by mind is power last updated on 10/Feb/20
withe pleasur
$${withe}\:{pleasur} \\ $$
Commented by john santu last updated on 10/Feb/20
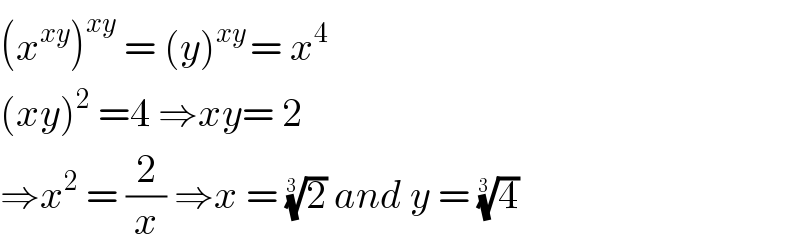
(x^(xy) )^(xy) = (y)^(xy ) = x^4 (xy)^2 =4 ⇒xy= 2 ⇒x^2 = (2/x) ⇒x = (2)^(1/(3 )) and y = (4)^(1/(3 ))
$$\left({x}^{{xy}} \right)^{{xy}} \:=\:\left({y}\right)^{{xy}\:} =\:{x}^{\mathrm{4}} \\ $$$$\left({xy}\right)^{\mathrm{2}} \:=\mathrm{4}\:\Rightarrow{xy}=\:\mathrm{2} \\ $$$$\Rightarrow{x}^{\mathrm{2}} \:=\:\frac{\mathrm{2}}{{x}}\:\Rightarrow{x}\:=\:\sqrt[{\mathrm{3}\:}]{\mathrm{2}}\:{and}\:{y}\:=\:\sqrt[{\mathrm{3}\:}]{\mathrm{4}}\: \\ $$
Commented by john santu last updated on 10/Feb/20
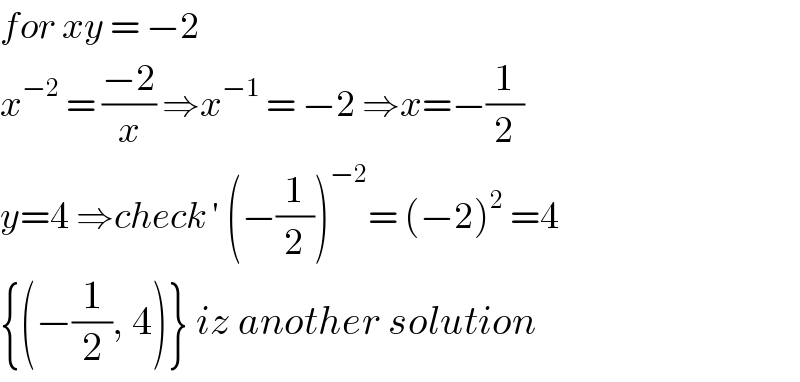
for xy = −2 x^(−2) = ((−2)/x) ⇒x^(−1) = −2 ⇒x=−(1/2) y=4 ⇒check ′ (−(1/2))^(−2) = (−2)^2 =4 {(−(1/2), 4)} iz another solution
$${for}\:{xy}\:=\:−\mathrm{2}\: \\ $$$${x}^{−\mathrm{2}} \:=\:\frac{−\mathrm{2}}{{x}}\:\Rightarrow{x}^{−\mathrm{1}} \:=\:−\mathrm{2}\:\Rightarrow{x}=−\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${y}=\mathrm{4}\:\Rightarrow{check}\:'\:\left(−\frac{\mathrm{1}}{\mathrm{2}}\right)^{−\mathrm{2}} =\:\left(−\mathrm{2}\right)^{\mathrm{2}} \:=\mathrm{4} \\ $$$$\left\{\left(−\frac{\mathrm{1}}{\mathrm{2}},\:\mathrm{4}\right)\right\}\:{iz}\:{another}\:{solution} \\ $$
Commented by mr W last updated on 10/Feb/20
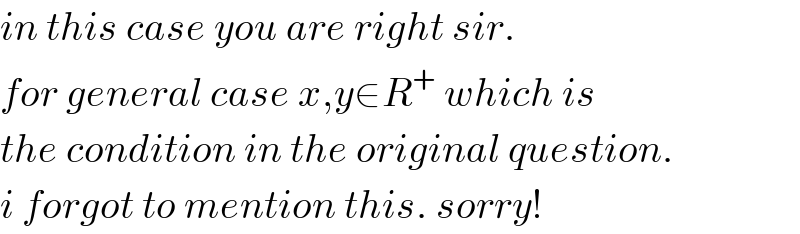
in this case you are right sir. for general case x,y∈R^+ which is the condition in the original question. i forgot to mention this. sorry!
$${in}\:{this}\:{case}\:{you}\:{are}\:{right}\:{sir}. \\ $$$${for}\:{general}\:{case}\:{x},{y}\in{R}^{+} \:{which}\:{is} \\ $$$${the}\:{condition}\:{in}\:{the}\:{original}\:{question}. \\ $$$${i}\:{forgot}\:{to}\:{mention}\:{this}.\:{sorry}! \\ $$
Commented by john santu last updated on 11/Feb/20
ok sir
$${ok}\:{sir} \\ $$
Answered by mr W last updated on 10/Feb/20
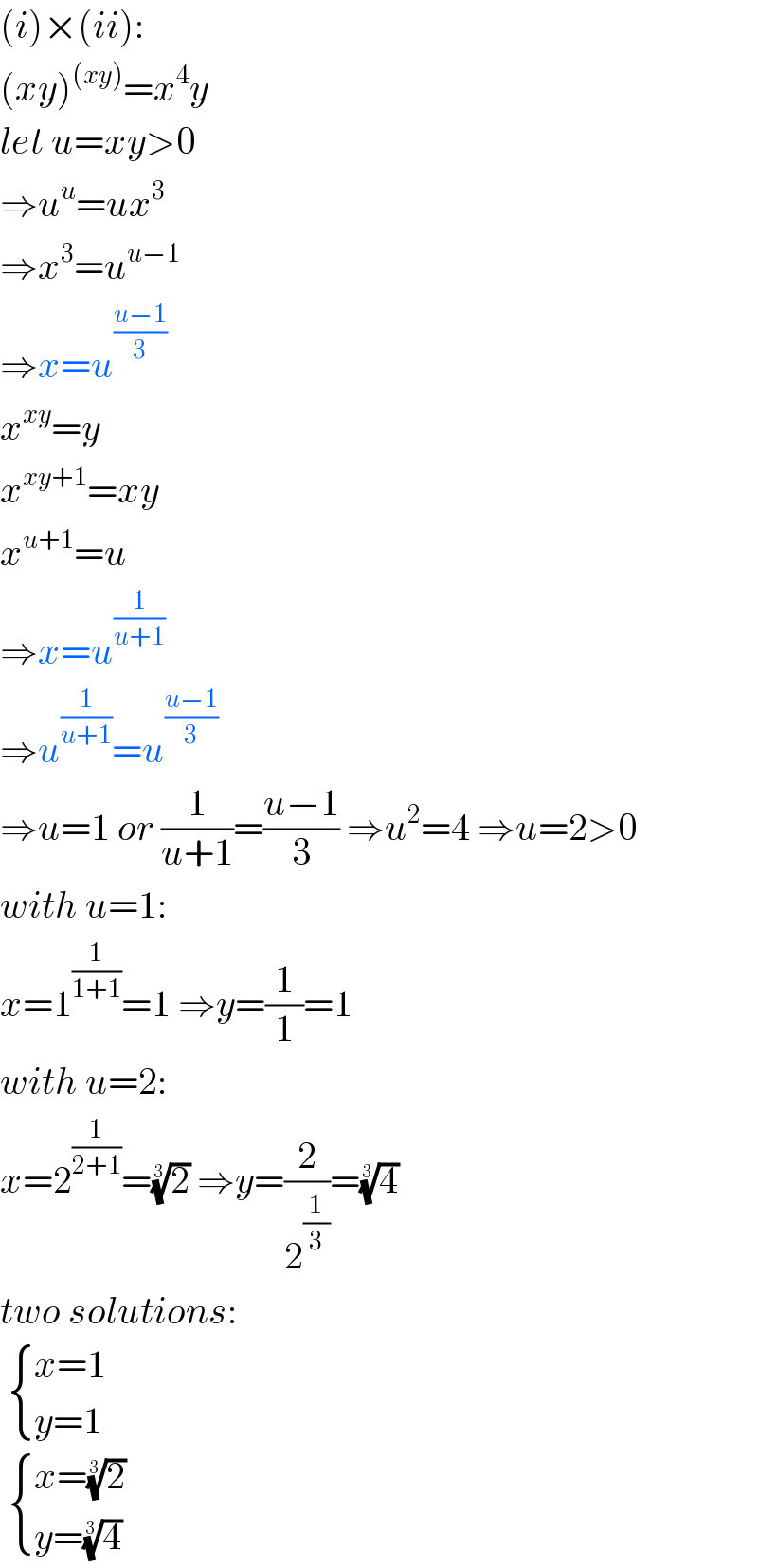
(i)×(ii): (xy)^((xy)) =x^4 y let u=xy>0 ⇒u^u =ux^3 ⇒x^3 =u^(u−1) ⇒x=u^((u−1)/3) x^(xy) =y x^(xy+1) =xy x^(u+1) =u ⇒x=u^(1/(u+1)) ⇒u^(1/(u+1)) =u^((u−1)/3) ⇒u=1 or (1/(u+1))=((u−1)/3) ⇒u^2 =4 ⇒u=2>0 with u=1: x=1^(1/(1+1)) =1 ⇒y=(1/1)=1 with u=2: x=2^(1/(2+1)) =(2)^(1/3) ⇒y=(2/2^(1/3) )=(4)^(1/3) two solutions: { ((x=1)),((y=1)) :} { ((x=(2)^(1/3) )),((y=(4)^(1/3) )) :}
$$\left({i}\right)×\left({ii}\right): \\ $$$$\left({xy}\right)^{\left({xy}\right)} ={x}^{\mathrm{4}} {y} \\ $$$${let}\:{u}={xy}>\mathrm{0} \\ $$$$\Rightarrow{u}^{{u}} ={ux}^{\mathrm{3}} \\ $$$$\Rightarrow{x}^{\mathrm{3}} ={u}^{{u}−\mathrm{1}} \\ $$$$\Rightarrow{x}={u}^{\frac{{u}−\mathrm{1}}{\mathrm{3}}} \\ $$$${x}^{{xy}} ={y} \\ $$$${x}^{{xy}+\mathrm{1}} ={xy} \\ $$$${x}^{{u}+\mathrm{1}} ={u} \\ $$$$\Rightarrow{x}={u}^{\frac{\mathrm{1}}{{u}+\mathrm{1}}} \\ $$$$\Rightarrow{u}^{\frac{\mathrm{1}}{{u}+\mathrm{1}}} ={u}^{\frac{{u}−\mathrm{1}}{\mathrm{3}}} \\ $$$$\Rightarrow{u}=\mathrm{1}\:{or}\:\frac{\mathrm{1}}{{u}+\mathrm{1}}=\frac{{u}−\mathrm{1}}{\mathrm{3}}\:\Rightarrow{u}^{\mathrm{2}} =\mathrm{4}\:\Rightarrow{u}=\mathrm{2}>\mathrm{0} \\ $$$${with}\:{u}=\mathrm{1}: \\ $$$${x}=\mathrm{1}^{\frac{\mathrm{1}}{\mathrm{1}+\mathrm{1}}} =\mathrm{1}\:\Rightarrow{y}=\frac{\mathrm{1}}{\mathrm{1}}=\mathrm{1} \\ $$$${with}\:{u}=\mathrm{2}: \\ $$$${x}=\mathrm{2}^{\frac{\mathrm{1}}{\mathrm{2}+\mathrm{1}}} =\sqrt[{\mathrm{3}}]{\mathrm{2}}\:\Rightarrow{y}=\frac{\mathrm{2}}{\mathrm{2}^{\frac{\mathrm{1}}{\mathrm{3}}} }=\sqrt[{\mathrm{3}}]{\mathrm{4}} \\ $$$${two}\:{solutions}: \\ $$$$\:\begin{cases}{{x}=\mathrm{1}}\\{{y}=\mathrm{1}}\end{cases} \\ $$$$\:\begin{cases}{{x}=\sqrt[{\mathrm{3}}]{\mathrm{2}}}\\{{y}=\sqrt[{\mathrm{3}}]{\mathrm{4}}}\end{cases} \\ $$
Commented by john santu last updated on 10/Feb/20
three answer
$${three}\:{answer}\: \\ $$
Commented by mr W last updated on 11/Feb/20
i forgot to mention the condition in the original question: x,y∈R^+ . because for the functions x^(xy) and y^(xy) their domain is x>0 and y>0. only for special integer powers, x and y can also be negative. but for general cases x and y must be >0, for example if the second eqn. is y^(xy) =x^5 .
$${i}\:{forgot}\:{to}\:{mention}\:{the}\:{condition}\:{in} \\ $$$${the}\:{original}\:{question}:\:{x},{y}\in{R}^{+} .\:{because} \\ $$$${for}\:{the}\:{functions}\:{x}^{{xy}} \:{and}\:{y}^{{xy}} \:{their} \\ $$$${domain}\:{is}\:{x}>\mathrm{0}\:{and}\:{y}>\mathrm{0}.\:{only}\:{for} \\ $$$${special}\:{integer}\:{powers},\:{x}\:{and}\:{y} \\ $$$${can}\:{also}\:{be}\:{negative}.\:{but}\:{for}\:{general} \\ $$$${cases}\:{x}\:{and}\:{y}\:{must}\:{be}\:>\mathrm{0},\:{for}\:{example} \\ $$$${if}\:{the}\:{second}\:{eqn}.\:{is}\:{y}^{{xy}} ={x}^{\mathrm{5}} . \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *