Question Number 81308 by naka3546 last updated on 11/Feb/20

Commented by mr W last updated on 11/Feb/20

$$\mathrm{2104}? \\ $$
Commented by naka3546 last updated on 11/Feb/20
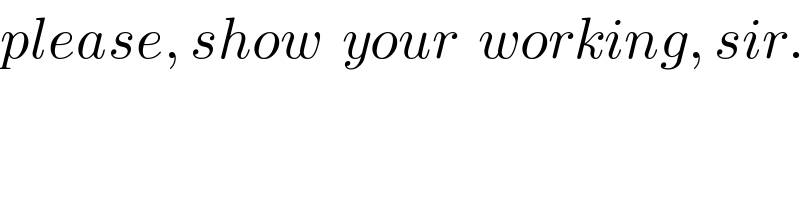
$${please},\:{show}\:\:{your}\:\:{working},\:{sir}. \\ $$
Answered by mr W last updated on 12/Feb/20
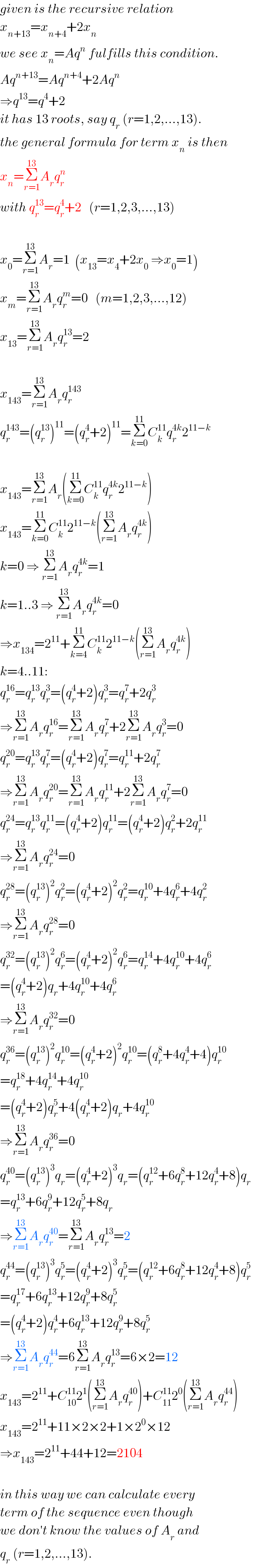
$${given}\:{is}\:{the}\:{recursive}\:{relation} \\ $$$${x}_{{n}+\mathrm{13}} ={x}_{{n}+\mathrm{4}} +\mathrm{2}{x}_{{n}} \\ $$$${we}\:{see}\:{x}_{{n}} ={Aq}^{{n}} \:{fulfills}\:{this}\:{condition}. \\ $$$${Aq}^{{n}+\mathrm{13}} ={Aq}^{{n}+\mathrm{4}} +\mathrm{2}{Aq}^{{n}} \\ $$$$\Rightarrow{q}^{\mathrm{13}} ={q}^{\mathrm{4}} +\mathrm{2} \\ $$$${it}\:{has}\:\mathrm{13}\:{roots},\:{say}\:{q}_{{r}} \:\left({r}=\mathrm{1},\mathrm{2},…,\mathrm{13}\right). \\ $$$${the}\:{general}\:{formula}\:{for}\:{term}\:{x}_{{n}} \:{is}\:{then} \\ $$$${x}_{{n}} =\underset{{r}=\mathrm{1}} {\overset{\mathrm{13}} {\sum}}{A}_{{r}} {q}_{{r}} ^{{n}} \\ $$$${with}\:{q}_{{r}} ^{\mathrm{13}} ={q}_{{r}} ^{\mathrm{4}} +\mathrm{2}\:\:\:\left({r}=\mathrm{1},\mathrm{2},\mathrm{3},…,\mathrm{13}\right) \\ $$$$ \\ $$$${x}_{\mathrm{0}} =\underset{{r}=\mathrm{1}} {\overset{\mathrm{13}} {\sum}}{A}_{{r}} =\mathrm{1}\:\:\left({x}_{\mathrm{13}} ={x}_{\mathrm{4}} +\mathrm{2}{x}_{\mathrm{0}} \:\Rightarrow{x}_{\mathrm{0}} =\mathrm{1}\right) \\ $$$${x}_{{m}} =\underset{{r}=\mathrm{1}} {\overset{\mathrm{13}} {\sum}}{A}_{{r}} {q}_{{r}} ^{{m}} =\mathrm{0}\:\:\:\left({m}=\mathrm{1},\mathrm{2},\mathrm{3},…,\mathrm{12}\right) \\ $$$${x}_{\mathrm{13}} =\underset{{r}=\mathrm{1}} {\overset{\mathrm{13}} {\sum}}{A}_{{r}} {q}_{{r}} ^{\mathrm{13}} =\mathrm{2} \\ $$$$ \\ $$$${x}_{\mathrm{143}} =\underset{{r}=\mathrm{1}} {\overset{\mathrm{13}} {\sum}}{A}_{{r}} {q}_{{r}} ^{\mathrm{143}} \\ $$$${q}_{{r}} ^{\mathrm{143}} =\left({q}_{{r}} ^{\mathrm{13}} \right)^{\mathrm{11}} =\left({q}_{{r}} ^{\mathrm{4}} +\mathrm{2}\right)^{\mathrm{11}} =\underset{{k}=\mathrm{0}} {\overset{\mathrm{11}} {\sum}}{C}_{{k}} ^{\mathrm{11}} {q}_{{r}} ^{\mathrm{4}{k}} \mathrm{2}^{\mathrm{11}−{k}} \\ $$$$ \\ $$$${x}_{\mathrm{143}} =\underset{{r}=\mathrm{1}} {\overset{\mathrm{13}} {\sum}}{A}_{{r}} \left(\underset{{k}=\mathrm{0}} {\overset{\mathrm{11}} {\sum}}{C}_{{k}} ^{\mathrm{11}} {q}_{{r}} ^{\mathrm{4}{k}} \mathrm{2}^{\mathrm{11}−{k}} \right) \\ $$$${x}_{\mathrm{143}} =\underset{{k}=\mathrm{0}} {\overset{\mathrm{11}} {\sum}}{C}_{{k}} ^{\mathrm{11}} \mathrm{2}^{\mathrm{11}−{k}} \left(\underset{{r}=\mathrm{1}} {\overset{\mathrm{13}} {\sum}}{A}_{{r}} {q}_{{r}} ^{\mathrm{4}{k}} \right) \\ $$$${k}=\mathrm{0}\:\Rightarrow\:\underset{{r}=\mathrm{1}} {\overset{\mathrm{13}} {\sum}}{A}_{{r}} {q}_{{r}} ^{\mathrm{4}{k}} =\mathrm{1} \\ $$$${k}=\mathrm{1}..\mathrm{3}\:\Rightarrow\:\underset{{r}=\mathrm{1}} {\overset{\mathrm{13}} {\sum}}{A}_{{r}} {q}_{{r}} ^{\mathrm{4}{k}} =\mathrm{0} \\ $$$$\Rightarrow{x}_{\mathrm{134}} =\mathrm{2}^{\mathrm{11}} +\underset{{k}=\mathrm{4}} {\overset{\mathrm{11}} {\sum}}{C}_{{k}} ^{\mathrm{11}} \mathrm{2}^{\mathrm{11}−{k}} \left(\underset{{r}=\mathrm{1}} {\overset{\mathrm{13}} {\sum}}{A}_{{r}} {q}_{{r}} ^{\mathrm{4}{k}} \right) \\ $$$${k}=\mathrm{4}..\mathrm{11}: \\ $$$${q}_{{r}} ^{\mathrm{16}} ={q}_{{r}} ^{\mathrm{13}} {q}_{{r}} ^{\mathrm{3}} =\left({q}_{{r}} ^{\mathrm{4}} +\mathrm{2}\right){q}_{{r}} ^{\mathrm{3}} ={q}_{{r}} ^{\mathrm{7}} +\mathrm{2}{q}_{{r}} ^{\mathrm{3}} \\ $$$$\Rightarrow\underset{{r}=\mathrm{1}} {\overset{\mathrm{13}} {\sum}}{A}_{{r}} {q}_{{r}} ^{\mathrm{16}} =\underset{{r}=\mathrm{1}} {\overset{\mathrm{13}} {\sum}}{A}_{{r}} {q}_{{r}} ^{\mathrm{7}} +\mathrm{2}\underset{{r}=\mathrm{1}} {\overset{\mathrm{13}} {\sum}}{A}_{{r}} {q}_{{r}} ^{\mathrm{3}} =\mathrm{0} \\ $$$${q}_{{r}} ^{\mathrm{20}} ={q}_{{r}} ^{\mathrm{13}} {q}_{{r}} ^{\mathrm{7}} =\left({q}_{{r}} ^{\mathrm{4}} +\mathrm{2}\right){q}_{{r}} ^{\mathrm{7}} ={q}_{{r}} ^{\mathrm{11}} +\mathrm{2}{q}_{{r}} ^{\mathrm{7}} \\ $$$$\Rightarrow\underset{{r}=\mathrm{1}} {\overset{\mathrm{13}} {\sum}}{A}_{{r}} {q}_{{r}} ^{\mathrm{20}} =\underset{{r}=\mathrm{1}} {\overset{\mathrm{13}} {\sum}}{A}_{{r}} {q}_{{r}} ^{\mathrm{11}} +\mathrm{2}\underset{{r}=\mathrm{1}} {\overset{\mathrm{13}} {\sum}}{A}_{{r}} {q}_{{r}} ^{\mathrm{7}} =\mathrm{0} \\ $$$${q}_{{r}} ^{\mathrm{24}} ={q}_{{r}} ^{\mathrm{13}} {q}_{{r}} ^{\mathrm{11}} =\left({q}_{{r}} ^{\mathrm{4}} +\mathrm{2}\right){q}_{{r}} ^{\mathrm{11}} =\left({q}_{{r}} ^{\mathrm{4}} +\mathrm{2}\right){q}_{{r}} ^{\mathrm{2}} +\mathrm{2}{q}_{{r}} ^{\mathrm{11}} \\ $$$$\Rightarrow\underset{{r}=\mathrm{1}} {\overset{\mathrm{13}} {\sum}}{A}_{{r}} {q}_{{r}} ^{\mathrm{24}} =\mathrm{0} \\ $$$${q}_{{r}} ^{\mathrm{28}} =\left({q}_{{r}} ^{\mathrm{13}} \right)^{\mathrm{2}} {q}_{{r}} ^{\mathrm{2}} =\left({q}_{{r}} ^{\mathrm{4}} +\mathrm{2}\right)^{\mathrm{2}} {q}_{{r}} ^{\mathrm{2}} ={q}_{{r}} ^{\mathrm{10}} +\mathrm{4}{q}_{{r}} ^{\mathrm{6}} +\mathrm{4}{q}_{{r}} ^{\mathrm{2}} \\ $$$$\Rightarrow\underset{{r}=\mathrm{1}} {\overset{\mathrm{13}} {\sum}}{A}_{{r}} {q}_{{r}} ^{\mathrm{28}} =\mathrm{0} \\ $$$${q}_{{r}} ^{\mathrm{32}} =\left({q}_{{r}} ^{\mathrm{13}} \right)^{\mathrm{2}} {q}_{{r}} ^{\mathrm{6}} =\left({q}_{{r}} ^{\mathrm{4}} +\mathrm{2}\right)^{\mathrm{2}} {q}_{{r}} ^{\mathrm{6}} ={q}_{{r}} ^{\mathrm{14}} +\mathrm{4}{q}_{{r}} ^{\mathrm{10}} +\mathrm{4}{q}_{{r}} ^{\mathrm{6}} \\ $$$$=\left({q}_{{r}} ^{\mathrm{4}} +\mathrm{2}\right){q}_{{r}} +\mathrm{4}{q}_{{r}} ^{\mathrm{10}} +\mathrm{4}{q}_{{r}} ^{\mathrm{6}} \\ $$$$\Rightarrow\underset{{r}=\mathrm{1}} {\overset{\mathrm{13}} {\sum}}{A}_{{r}} {q}_{{r}} ^{\mathrm{32}} =\mathrm{0} \\ $$$${q}_{{r}} ^{\mathrm{36}} =\left({q}_{{r}} ^{\mathrm{13}} \right)^{\mathrm{2}} {q}_{{r}} ^{\mathrm{10}} =\left({q}_{{r}} ^{\mathrm{4}} +\mathrm{2}\right)^{\mathrm{2}} {q}_{{r}} ^{\mathrm{10}} =\left({q}_{{r}} ^{\mathrm{8}} +\mathrm{4}{q}_{{r}} ^{\mathrm{4}} +\mathrm{4}\right){q}_{{r}} ^{\mathrm{10}} \\ $$$$={q}_{{r}} ^{\mathrm{18}} +\mathrm{4}{q}_{{r}} ^{\mathrm{14}} +\mathrm{4}{q}_{{r}} ^{\mathrm{10}} \\ $$$$=\left({q}_{{r}} ^{\mathrm{4}} +\mathrm{2}\right){q}_{{r}} ^{\mathrm{5}} +\mathrm{4}\left({q}_{{r}} ^{\mathrm{4}} +\mathrm{2}\right){q}_{{r}} +\mathrm{4}{q}_{{r}} ^{\mathrm{10}} \\ $$$$\Rightarrow\underset{{r}=\mathrm{1}} {\overset{\mathrm{13}} {\sum}}{A}_{{r}} {q}_{{r}} ^{\mathrm{36}} =\mathrm{0} \\ $$$${q}_{{r}} ^{\mathrm{40}} =\left({q}_{{r}} ^{\mathrm{13}} \right)^{\mathrm{3}} {q}_{{r}} =\left({q}_{{r}} ^{\mathrm{4}} +\mathrm{2}\right)^{\mathrm{3}} {q}_{{r}} =\left({q}_{{r}} ^{\mathrm{12}} +\mathrm{6}{q}_{{r}} ^{\mathrm{8}} +\mathrm{12}{q}_{{r}} ^{\mathrm{4}} +\mathrm{8}\right){q}_{{r}} \\ $$$$={q}_{{r}} ^{\mathrm{13}} +\mathrm{6}{q}_{{r}} ^{\mathrm{9}} +\mathrm{12}{q}_{{r}} ^{\mathrm{5}} +\mathrm{8}{q}_{{r}} \: \\ $$$$\Rightarrow\underset{{r}=\mathrm{1}} {\overset{\mathrm{13}} {\sum}}{A}_{{r}} {q}_{{r}} ^{\mathrm{40}} =\underset{{r}=\mathrm{1}} {\overset{\mathrm{13}} {\sum}}{A}_{{r}} {q}_{{r}} ^{\mathrm{13}} =\mathrm{2} \\ $$$${q}_{{r}} ^{\mathrm{44}} =\left({q}_{{r}} ^{\mathrm{13}} \right)^{\mathrm{3}} {q}_{{r}} ^{\mathrm{5}} =\left({q}_{{r}} ^{\mathrm{4}} +\mathrm{2}\right)^{\mathrm{3}} {q}_{{r}} ^{\mathrm{5}} =\left({q}_{{r}} ^{\mathrm{12}} +\mathrm{6}{q}_{{r}} ^{\mathrm{8}} +\mathrm{12}{q}_{{r}} ^{\mathrm{4}} +\mathrm{8}\right){q}_{{r}} ^{\mathrm{5}} \: \\ $$$$={q}_{{r}} ^{\mathrm{17}} +\mathrm{6}{q}_{{r}} ^{\mathrm{13}} +\mathrm{12}{q}_{{r}} ^{\mathrm{9}} +\mathrm{8}{q}_{{r}} ^{\mathrm{5}} \\ $$$$=\left({q}_{{r}} ^{\mathrm{4}} +\mathrm{2}\right){q}_{{r}} ^{\mathrm{4}} +\mathrm{6}{q}_{{r}} ^{\mathrm{13}} +\mathrm{12}{q}_{{r}} ^{\mathrm{9}} +\mathrm{8}{q}_{{r}} ^{\mathrm{5}} \\ $$$$\Rightarrow\underset{{r}=\mathrm{1}} {\overset{\mathrm{13}} {\sum}}{A}_{{r}} {q}_{{r}} ^{\mathrm{44}} =\mathrm{6}\underset{{r}=\mathrm{1}} {\overset{\mathrm{13}} {\sum}}{A}_{{r}} {q}_{{r}} ^{\mathrm{13}} =\mathrm{6}×\mathrm{2}=\mathrm{12} \\ $$$${x}_{\mathrm{143}} =\mathrm{2}^{\mathrm{11}} +{C}_{\mathrm{10}} ^{\mathrm{11}} \mathrm{2}^{\mathrm{1}} \left(\underset{{r}=\mathrm{1}} {\overset{\mathrm{13}} {\sum}}{A}_{{r}} {q}_{{r}} ^{\mathrm{40}} \right)+{C}_{\mathrm{11}} ^{\mathrm{11}} \mathrm{2}^{\mathrm{0}} \left(\underset{{r}=\mathrm{1}} {\overset{\mathrm{13}} {\sum}}{A}_{{r}} {q}_{{r}} ^{\mathrm{44}} \right) \\ $$$${x}_{\mathrm{143}} =\mathrm{2}^{\mathrm{11}} +\mathrm{11}×\mathrm{2}×\mathrm{2}+\mathrm{1}×\mathrm{2}^{\mathrm{0}} ×\mathrm{12} \\ $$$$\Rightarrow{x}_{\mathrm{143}} =\mathrm{2}^{\mathrm{11}} +\mathrm{44}+\mathrm{12}=\mathrm{2104} \\ $$$$ \\ $$$${in}\:{this}\:{way}\:{we}\:{can}\:{calculate}\:{every} \\ $$$${term}\:{of}\:{the}\:{sequence}\:{even}\:{though} \\ $$$${we}\:{don}'{t}\:{know}\:{the}\:{values}\:{of}\:{A}_{{r}} \:{and} \\ $$$${q}_{{r}} \:\left({r}=\mathrm{1},\mathrm{2},…,\mathrm{13}\right). \\ $$
