Question-81311

Question Number 81311 by M±th+et£s last updated on 11/Feb/20

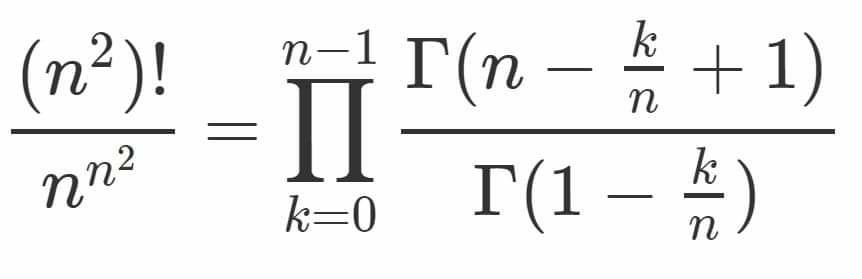
Commented by mind is power last updated on 11/Feb/20

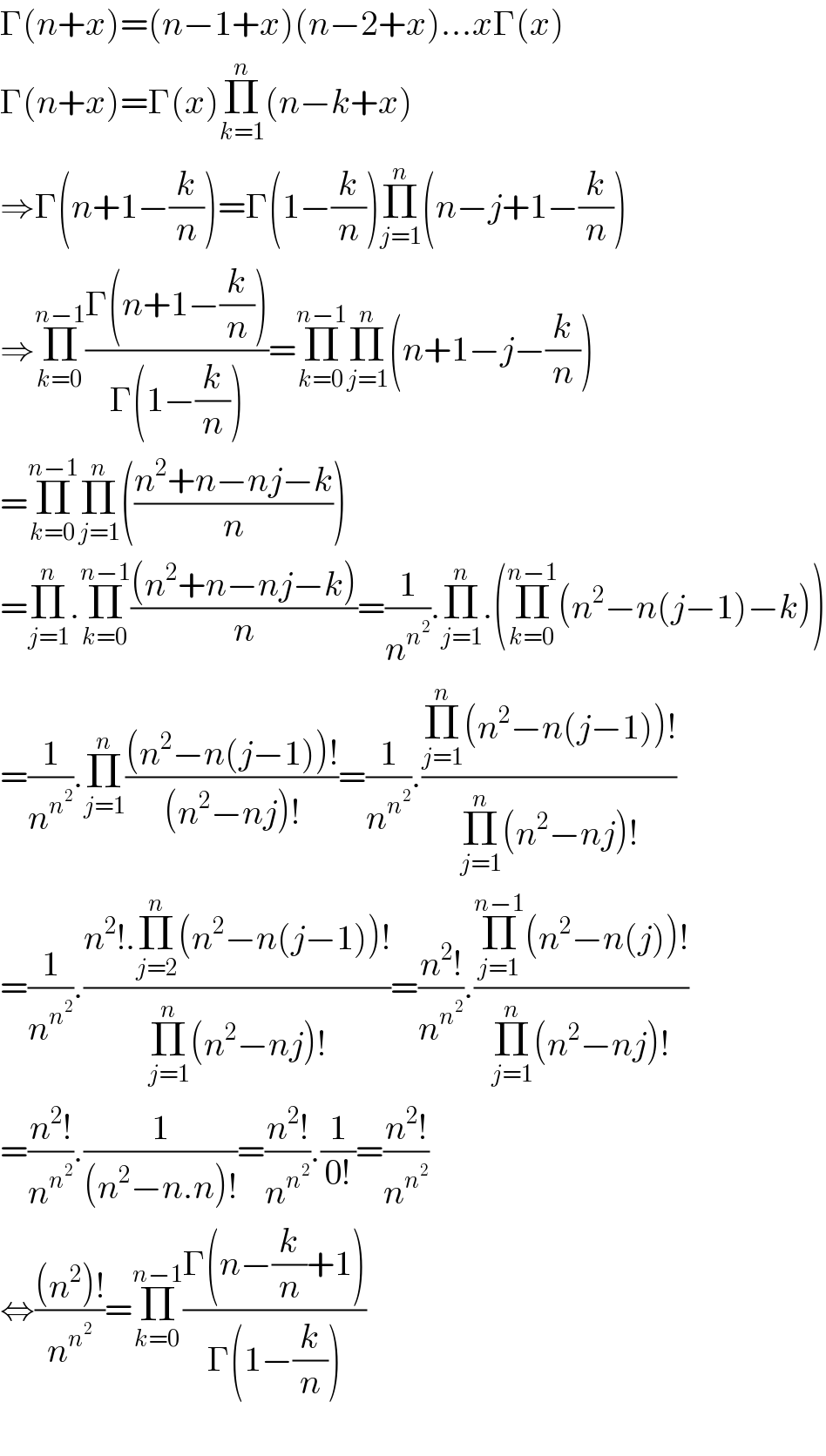
Γ(n+x)=(n−1+x)(n−2+x)...xΓ(x) Γ(n+x)=Γ(x)Π_(k=1) ^n (n−k+x) ⇒Γ(n+1−(k/n))=Γ(1−(k/n))Π_(j=1) ^n (n−j+1−(k/n)) ⇒Π_(k=0) ^(n−1) ((Γ(n+1−(k/n)))/(Γ(1−(k/n))))=Π_(k=0) ^(n−1) Π_(j=1) ^n (n+1−j−(k/n)) =Π_(k=0) ^(n−1) Π_(j=1) ^n (((n^2 +n−nj−k)/n)) =Π_(j=1) ^n .Π_(k=0) ^(n−1) (((n^2 +n−nj−k))/n)=(1/n^n^2 ).Π_(j=1) ^n .(Π_(k=0) ^(n−1) (n^2 −n(j−1)−k)) =(1/n^n^2 ).Π_(j=1) ^n (((n^2 −n(j−1))!)/((n^2 −nj)!))=(1/n^n^2 ).((Π_(j=1) ^n (n^2 −n(j−1))!)/(Π_(j=1) ^n (n^2 −nj)!)) =(1/n^n^2 ).((n^2 !.Π_(j=2) ^n (n^2 −n(j−1))!)/(Π_(j=1) ^n (n^2 −nj)!))=((n^2 !)/n^n^2 ).((Π_(j=1) ^(n−1) (n^2 −n(j))!)/(Π_(j=1) ^n (n^2 −nj)!)) =((n^2 !)/n^n^2 ).(1/((n^2 −n.n)!))=((n^2 !)/n^n^2 ).(1/(0!))=((n^2 !)/n^n^2 ) ⇔(((n^2 )!)/n^n^2 )=Π_(k=0) ^(n−1) ((Γ(n−(k/n)+1))/(Γ(1−(k/n))))

$$\Gamma\left({n}+{x}\right)=\left({n}−\mathrm{1}+{x}\right)\left({n}−\mathrm{2}+{x}\right)…{x}\Gamma\left({x}\right)\:\: \\ $$$$\Gamma\left({n}+{x}\right)=\Gamma\left({x}\right)\underset{{k}=\mathrm{1}} {\overset{{n}} {\prod}}\left({n}−{k}+{x}\right) \\ $$$$\Rightarrow\Gamma\left({n}+\mathrm{1}−\frac{{k}}{{n}}\right)=\Gamma\left(\mathrm{1}−\frac{{k}}{{n}}\right)\underset{{j}=\mathrm{1}} {\overset{{n}} {\prod}}\left({n}−{j}+\mathrm{1}−\frac{{k}}{{n}}\right) \\ $$$$\Rightarrow\underset{{k}=\mathrm{0}} {\overset{{n}−\mathrm{1}} {\prod}}\frac{\Gamma\left({n}+\mathrm{1}−\frac{{k}}{{n}}\right)}{\Gamma\left(\mathrm{1}−\frac{{k}}{{n}}\right)}=\underset{{k}=\mathrm{0}} {\overset{{n}−\mathrm{1}} {\prod}}\underset{{j}=\mathrm{1}} {\overset{{n}} {\prod}}\left({n}+\mathrm{1}−{j}−\frac{{k}}{{n}}\right) \\ $$$$=\underset{{k}=\mathrm{0}} {\overset{{n}−\mathrm{1}} {\prod}}\underset{{j}=\mathrm{1}} {\overset{{n}} {\prod}}\left(\frac{{n}^{\mathrm{2}} +{n}−{nj}−{k}}{{n}}\right) \\ $$$$=\underset{{j}=\mathrm{1}} {\overset{{n}} {\prod}}.\underset{{k}=\mathrm{0}} {\overset{{n}−\mathrm{1}} {\prod}}\frac{\left({n}^{\mathrm{2}} +{n}−{nj}−{k}\right)}{{n}}=\frac{\mathrm{1}}{{n}^{{n}^{\mathrm{2}} } }.\underset{{j}=\mathrm{1}} {\overset{{n}} {\prod}}.\left(\underset{{k}=\mathrm{0}} {\overset{{n}−\mathrm{1}} {\prod}}\left({n}^{\mathrm{2}} −{n}\left({j}−\mathrm{1}\right)−{k}\right)\right) \\ $$$$=\frac{\mathrm{1}}{{n}^{{n}^{\mathrm{2}} } }.\underset{{j}=\mathrm{1}} {\overset{{n}} {\prod}}\frac{\left({n}^{\mathrm{2}} −{n}\left({j}−\mathrm{1}\right)\right)!}{\left({n}^{\mathrm{2}} −{nj}\right)!}=\frac{\mathrm{1}}{{n}^{{n}^{\mathrm{2}} } }.\frac{\underset{{j}=\mathrm{1}} {\overset{{n}} {\prod}}\left({n}^{\mathrm{2}} −{n}\left({j}−\mathrm{1}\right)\right)!}{\underset{{j}=\mathrm{1}} {\overset{{n}} {\prod}}\left({n}^{\mathrm{2}} −{nj}\right)!} \\ $$$$=\frac{\mathrm{1}}{{n}^{{n}^{\mathrm{2}} } }.\frac{{n}^{\mathrm{2}} !.\underset{{j}=\mathrm{2}} {\overset{{n}} {\prod}}\left({n}^{\mathrm{2}} −{n}\left({j}−\mathrm{1}\right)\right)!}{\underset{{j}=\mathrm{1}} {\overset{{n}} {\prod}}\left({n}^{\mathrm{2}} −{nj}\right)!}=\frac{{n}^{\mathrm{2}} !}{{n}^{{n}^{\mathrm{2}} } }.\frac{\underset{{j}=\mathrm{1}} {\overset{{n}−\mathrm{1}} {\prod}}\left({n}^{\mathrm{2}} −{n}\left({j}\right)\right)!}{\underset{{j}=\mathrm{1}} {\overset{{n}} {\prod}}\left({n}^{\mathrm{2}} −{nj}\right)!} \\ $$$$=\frac{{n}^{\mathrm{2}} !}{{n}^{{n}^{\mathrm{2}} } }.\frac{\mathrm{1}}{\left({n}^{\mathrm{2}} −{n}.{n}\right)!}=\frac{{n}^{\mathrm{2}} !}{{n}^{{n}^{\mathrm{2}} } }.\frac{\mathrm{1}}{\mathrm{0}!}=\frac{{n}^{\mathrm{2}} !}{{n}^{{n}^{\mathrm{2}} } } \\ $$$$\Leftrightarrow\frac{\left({n}^{\mathrm{2}} \right)!}{{n}^{{n}^{\mathrm{2}} } }=\underset{{k}=\mathrm{0}} {\overset{{n}−\mathrm{1}} {\prod}}\frac{\Gamma\left({n}−\frac{{k}}{{n}}+\mathrm{1}\right)}{\Gamma\left(\mathrm{1}−\frac{{k}}{{n}}\right)} \\ $$$$ \\ $$

Commented by M±th+et£s last updated on 11/Feb/20

$$\mathrm{god}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$

Commented by mind is power last updated on 11/Feb/20

$${y}'{re}\:{Welcom} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply