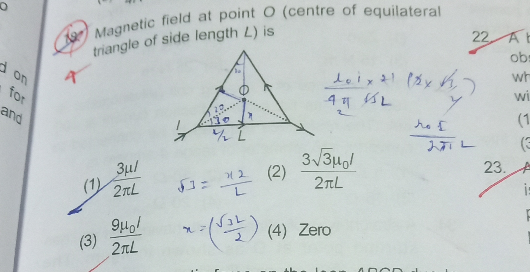
Question Number 81319 by rose last updated on 11/Feb/20
Answered by ajfour last updated on 12/Feb/20
Commented by ajfour last updated on 12/Feb/20

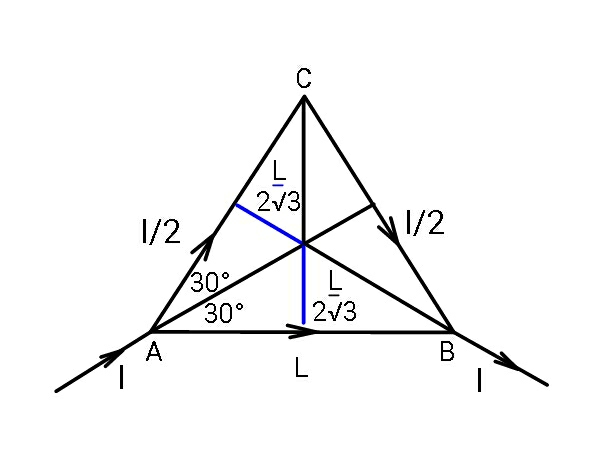
$$\bar {{B}}_{{AB}} =\frac{\mu_{\mathrm{0}} \left(\mathrm{2}{I}/\mathrm{3}\right)}{\mathrm{2}\pi\left(\frac{{L}}{\mathrm{2}\sqrt{\mathrm{3}}}\right)}\left(\frac{\mathrm{cos}\:\mathrm{30}°+\mathrm{cos}\:\mathrm{30}°}{\mathrm{2}}\right) \\ $$$$\:\:\:\:\:=\:\frac{\mathrm{2}\mu_{\mathrm{0}} {I}}{\mathrm{2}\pi{L}}\: \\ $$$$\bar {{B}}_{{AC}} +\bar {{B}}_{{BC}} =\:\mathrm{2}×\frac{\mu_{\mathrm{0}} \left({I}/\mathrm{3}\right)}{\mathrm{2}\pi\left(\frac{{L}}{\mathrm{2}\sqrt{\mathrm{3}}}\right)}\left(\frac{\mathrm{cos}\:\mathrm{30}°+\mathrm{cos}\:\mathrm{30}°}{\mathrm{2}}\right) \\ $$$$\:\:\:\:\:\:=\:\frac{\mu_{\mathrm{0}} {I}}{\mathrm{2}\pi{L}}\left(\mathrm{2}×\frac{\mathrm{1}}{\mathrm{3}}×\mathrm{2}\sqrt{\mathrm{3}}×\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\right)\:\square \\ $$$$\:\:\:\:=\:\frac{\mathrm{2}\mu_{\mathrm{0}} {I}}{\mathrm{2}\pi{L}}\:\square \\ $$$${hence} \\ $$$$\bar {{B}}_{{AB}} +\bar {{B}}_{{AC}} +\bar {{B}}_{{BC}} \:=\:\mathrm{0}\:. \\ $$
Commented by ajfour last updated on 12/Feb/20
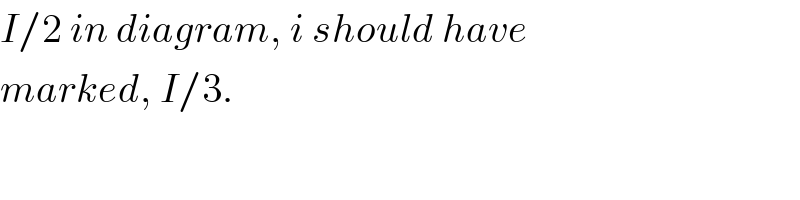
$${I}/\mathrm{2}\:{in}\:{diagram},\:{i}\:{should}\:{have} \\ $$$${marked},\:{I}/\mathrm{3}. \\ $$
