Question-81369

Question Number 81369 by mr W last updated on 12/Feb/20

Commented by mr W last updated on 12/Feb/20

This is a repost of Q81308. I found the answer through the following way, but it seems lengthy and complex. Are there any other standard methods?

$${This}\:{is}\:{a}\:{repost}\:{of}\:{Q}\mathrm{81308}. \\ $$$$ \\ $$$${I}\:{found}\:{the}\:{answer}\:{through}\:{the} \\ $$$${following}\:{way},\:{but}\:{it}\:{seems}\:{lengthy} \\ $$$${and}\:{complex}.\:{Are}\:{there}\:{any}\:{other} \\ $$$${standard}\:{methods}? \\ $$

Commented by mr W last updated on 12/Feb/20

Commented by MJS last updated on 12/Feb/20

I think there is no better method, but you made a consequent typo 134 instead of 143

$$\mathrm{I}\:\mathrm{think}\:\mathrm{there}\:\mathrm{is}\:\mathrm{no}\:\mathrm{better}\:\mathrm{method},\:\mathrm{but}\:\mathrm{you} \\ $$$$\mathrm{made}\:\mathrm{a}\:\mathrm{consequent}\:\mathrm{typo}\:\mathrm{134}\:\mathrm{instead}\:\mathrm{of}\:\mathrm{143} \\ $$

Commented by MJS last updated on 12/Feb/20

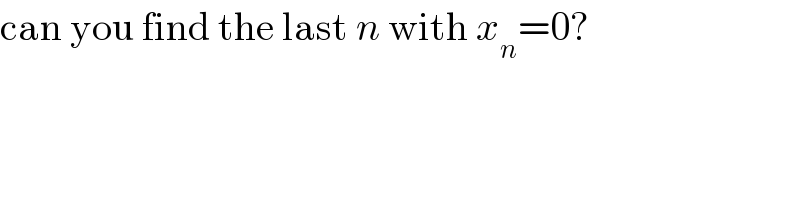
$$\mathrm{can}\:\mathrm{you}\:\mathrm{find}\:\mathrm{the}\:\mathrm{last}\:{n}\:\mathrm{with}\:{x}_{{n}} =\mathrm{0}? \\ $$

Commented by mr W last updated on 12/Feb/20

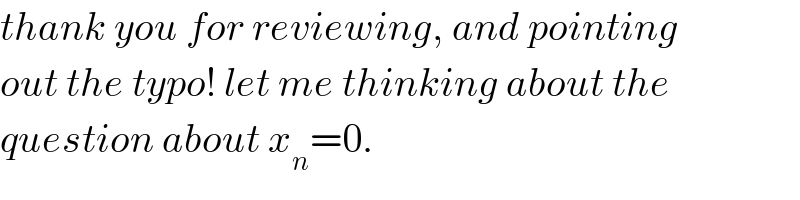
thank you for reviewing, and pointing out the typo! let me thinking about the question about x_n =0.

$${thank}\:{you}\:{for}\:{reviewing},\:{and}\:{pointing} \\ $$$${out}\:{the}\:{typo}!\:{let}\:{me}\:{thinking}\:{about}\:{the} \\ $$$${question}\:{about}\:{x}_{{n}} =\mathrm{0}. \\ $$

Commented by MJS last updated on 12/Feb/20

$$\mathrm{I}\:\mathrm{think}\:\mathrm{it}'\mathrm{s}\:\mathrm{at}\:{n}=\mathrm{108} \\ $$

Commented by mr W last updated on 12/Feb/20

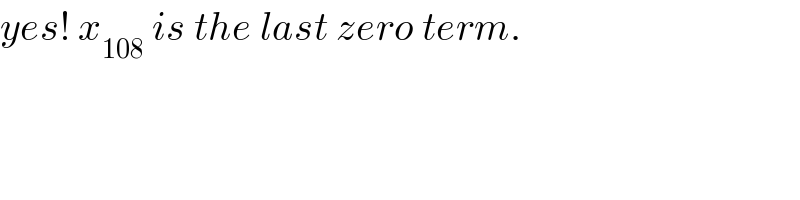
$${yes}!\:{x}_{\mathrm{108}} \:{is}\:{the}\:{last}\:{zero}\:{term}. \\ $$

Answered by MJS last updated on 12/Feb/20

$$\mathrm{2104} \\ $$

Answered by M±th+et£s last updated on 12/Feb/20

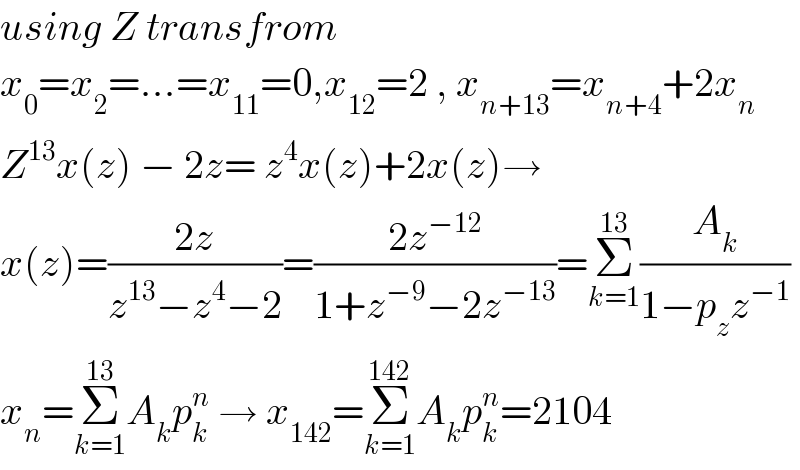
using Z transfrom x_0 =x_2 =...=x_(11) =0,x_(12) =2 , x_(n+13) =x_(n+4) +2x_n Z^(13) x(z) − 2z= z^4 x(z)+2x(z)→ x(z)=((2z)/(z^(13) −z^4 −2))=((2z^(−12) )/(1+z^(−9) −2z^(−13) ))=Σ_(k=1) ^(13) (A_k /(1−p_z z^(−1) )) x_n =Σ_(k=1) ^(13) A_k p_k ^n → x_(142) =Σ_(k=1) ^(142) A_k p_k ^n =2104

$${using}\:{Z}\:{transfrom} \\ $$$${x}_{\mathrm{0}} ={x}_{\mathrm{2}} =…={x}_{\mathrm{11}} =\mathrm{0},{x}_{\mathrm{12}} =\mathrm{2}\:,\:{x}_{{n}+\mathrm{13}} ={x}_{{n}+\mathrm{4}} +\mathrm{2}{x}_{{n}} \\ $$$${Z}^{\mathrm{13}} {x}\left({z}\right)\:−\:\mathrm{2}{z}=\:{z}^{\mathrm{4}} {x}\left({z}\right)+\mathrm{2}{x}\left({z}\right)\rightarrow \\ $$$${x}\left({z}\right)=\frac{\mathrm{2}{z}}{{z}^{\mathrm{13}} −{z}^{\mathrm{4}} −\mathrm{2}}=\frac{\mathrm{2}{z}^{−\mathrm{12}} }{\mathrm{1}+{z}^{−\mathrm{9}} −\mathrm{2}{z}^{−\mathrm{13}} }=\underset{{k}=\mathrm{1}} {\overset{\mathrm{13}} {\sum}}\frac{{A}_{{k}} }{\mathrm{1}−{p}_{{z}} {z}^{−\mathrm{1}} } \\ $$$${x}_{{n}} =\underset{{k}=\mathrm{1}} {\overset{\mathrm{13}} {\sum}}{A}_{{k}} {p}_{{k}} ^{{n}} \:\rightarrow\:{x}_{\mathrm{142}} =\underset{{k}=\mathrm{1}} {\overset{\mathrm{142}} {\sum}}{A}_{{k}} {p}_{{k}} ^{{n}} =\mathrm{2104} \\ $$

Commented by mr W last updated on 13/Feb/20

thank you! i have not understood yet. can you please check if there are any typos! please give more explanation to your last line and how you got 2104.

$${thank}\:{you}! \\ $$$${i}\:{have}\:{not}\:{understood}\:{yet}.\:{can}\:{you} \\ $$$${please}\:{check}\:{if}\:{there}\:{are}\:{any}\:{typos}! \\ $$$${please}\:{give}\:{more}\:{explanation}\:{to} \\ $$$${your}\:{last}\:{line}\:{and}\:{how}\:{you}\:{got}\:\mathrm{2104}. \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply