Question Number 81393 by ajfour last updated on 12/Feb/20

Commented by ajfour last updated on 12/Feb/20
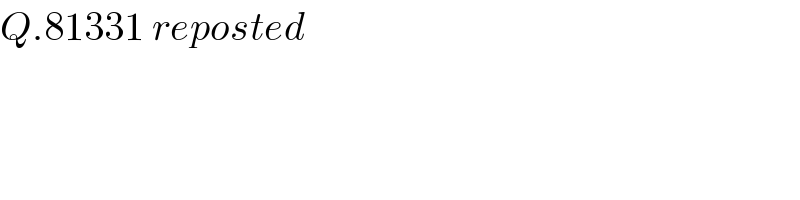
$${Q}.\mathrm{81331}\:{reposted} \\ $$
Answered by ajfour last updated on 12/Feb/20
Commented by mr W last updated on 12/Feb/20

Commented by ajfour last updated on 12/Feb/20

$${or}\:{it}\:{should}\:{be}\:{better}\:{to}\:{maximise} \\ $$$${area}\:{of}\:\bigtriangleup\:{shown}\:{in}\:{diagram}, \\ $$$${do}\:{you}\:{get}\:{my}\:{idea}\:{Sir}? \\ $$
Commented by mr W last updated on 12/Feb/20

Commented by mr W last updated on 12/Feb/20

$${diagram}\:{shows}\:{the}\:{triangle}\:{with} \\ $$$${maximum}\:{area}:\:{tangent}\:{at}\:{P}\:{is}\:// \\ $$$${to}\:{QR},\:{tangent}\:{at}\:{Q}\:{is}\://\:{to}\:{PR}\:{and} \\ $$$${tangent}\:{at}\:{R}\:{is}\://\:{to}\:{PQ}. \\ $$
Commented by ajfour last updated on 13/Feb/20
![with reference to diagram in this reposted question, let G(0,0) , O(−p,0), D(qcos θ,qsin θ) , E(rcos φ,−rsin φ). eq. of DE_(−) y−qsin θ=(((qsin θ+rsin φ)/(qcos θ−rcos φ)))(x−qcos θ) let y=0, x=l l=qcos θ−qsin θ(((qcos θ−rcos φ)/(qsin θ+rsin φ))) = ((qr(sin φcos θ+sin θcos φ))/(qsin θ+rsin φ)) A=(((p+l)(qsin θ+rsin φ))/2) ⇒ A=((p(qsin θ+rsin φ)+qrsin (θ+φ))/2) A=((pqsin θ+prsin φ+qr(sin θcos φ+cos θsin φ))/2) (∂A/∂θ)=0 , (∂A/∂φ)=0 ⇒ pqcos θ+qr(cos θcos φ−sin θsin φ)=0 & prcos φ+qr(−sin θsin φ+cos θcos φ)=0 ⇒ { ((r(tan θsin φ−cos φ)=p)),((q(tan φsin θ−cos θ)=p)) :} tan θtan φ=(p/r)sec φ+1=(p/q)sec θ+1 ⇒ rcos φ=qcos θ =x {otherwise A=(((p+x)/2))((√(q^2 −x^2 ))+(√(r^2 −x^2 ))) Now (dA/dx)=0 ⇒ (1/2)((√(q^2 −x^2 ))+(√(r^2 −x^2 ))) = ((x(p+x))/2)[(1/( (√(q^2 −x^2 ))))+(1/( (√(r^2 −x^2 ))))] (q^2 −x^2 )(r^2 −x^2 )=x^2 (p+x)^2 2px^3 +(p^2 +q^2 +r^2 )x^2 −q^2 r^2 =0 ⇒ (1/x^3 )−(((p^2 +q^2 +r^2 )/(q^2 r^2 )))(1/x)−((2p)/(q^2 r^2 ))=0 D={(p/(q^2 r^2 ))}^2 −(1/(27)){((p^2 +q^2 +r^2 )/(q^2 r^2 ))}^3 D(q^2 r^2 )^3 =p^2 q^2 r^2 −(((p^2 +q^2 +r^2 )/3))^3 Sir, what can be said about the sign of Discriminant here? } or rsec θ=qsec φ ⇒ (√(1+sec^2 θ))(√((r^2 /q^2 )sec^2 θ−1))=(p/q)sec θ+1 let sec θ=t (1+t^2 )(((r^2 t^2 )/q^2 )−1)=((p^2 t^2 )/q^2 )+((2pt)/q)+1 its a biquadratic... similarly for tan φ.... ...... AB=2(√((qcos θ+p)^2 +q^2 sin^2 θ)) BC=2(√((qcos θ−rcos φ)^2 +(qsin θ+rsin φ)^2 )) CA=2(√((rcos φ−p)^2 +r^2 sin^2 φ)) .](https://www.tinkutara.com/question/Q81411.png)
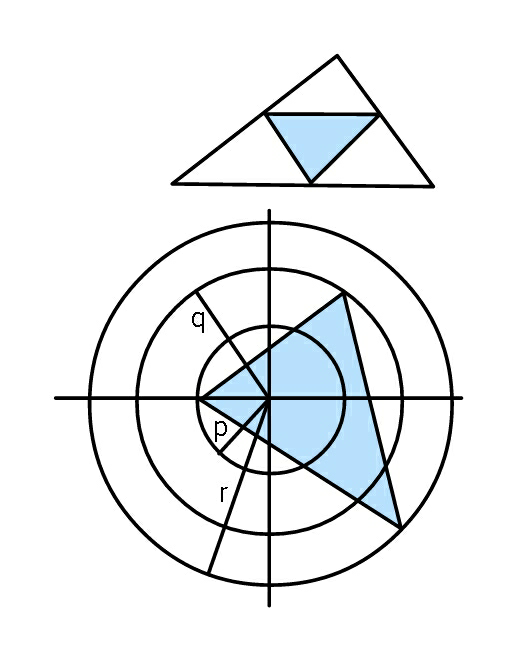
$${with}\:{reference}\:{to}\:{diagram}\:{in} \\ $$$${this}\:{reposted}\:{question},\:{let} \\ $$$${G}\left(\mathrm{0},\mathrm{0}\right)\:,\:{O}\left(−{p},\mathrm{0}\right), \\ $$$${D}\left({q}\mathrm{cos}\:\theta,{q}\mathrm{sin}\:\theta\right)\:,\:{E}\left({r}\mathrm{cos}\:\phi,−{r}\mathrm{sin}\:\phi\right). \\ $$$$\underset{−} {{eq}.\:{of}\:{DE}} \\ $$$${y}−{q}\mathrm{sin}\:\theta=\left(\frac{{q}\mathrm{sin}\:\theta+{r}\mathrm{sin}\:\phi}{{q}\mathrm{cos}\:\theta−{r}\mathrm{cos}\:\phi}\right)\left({x}−{q}\mathrm{cos}\:\theta\right) \\ $$$${let}\:{y}=\mathrm{0},\:{x}={l} \\ $$$${l}={q}\mathrm{cos}\:\theta−{q}\mathrm{sin}\:\theta\left(\frac{{q}\mathrm{cos}\:\theta−{r}\mathrm{cos}\:\phi}{{q}\mathrm{sin}\:\theta+{r}\mathrm{sin}\:\phi}\right) \\ $$$$\:=\:\frac{{qr}\left(\mathrm{sin}\:\phi\mathrm{cos}\:\theta+\mathrm{sin}\:\theta\mathrm{cos}\:\phi\right)}{{q}\mathrm{sin}\:\theta+{r}\mathrm{sin}\:\phi} \\ $$$${A}=\frac{\left({p}+{l}\right)\left({q}\mathrm{sin}\:\theta+{r}\mathrm{sin}\:\phi\right)}{\mathrm{2}} \\ $$$$\Rightarrow\:{A}=\frac{{p}\left({q}\mathrm{sin}\:\theta+{r}\mathrm{sin}\:\phi\right)+{qr}\mathrm{sin}\:\left(\theta+\phi\right)}{\mathrm{2}} \\ $$$${A}=\frac{{pq}\mathrm{sin}\:\theta+{pr}\mathrm{sin}\:\phi+{qr}\left(\mathrm{sin}\:\theta\mathrm{cos}\:\phi+\mathrm{cos}\:\theta\mathrm{sin}\:\phi\right)}{\mathrm{2}} \\ $$$$\frac{\partial{A}}{\partial\theta}=\mathrm{0}\:,\:\frac{\partial{A}}{\partial\phi}=\mathrm{0} \\ $$$$\Rightarrow\:{pq}\mathrm{cos}\:\theta+{qr}\left(\mathrm{cos}\:\theta\mathrm{cos}\:\phi−\mathrm{sin}\:\theta\mathrm{sin}\:\phi\right)=\mathrm{0} \\ $$$$\&\:\:{pr}\mathrm{cos}\:\phi+{qr}\left(−\mathrm{sin}\:\theta\mathrm{sin}\:\phi+\mathrm{cos}\:\theta\mathrm{cos}\:\phi\right)=\mathrm{0} \\ $$$$\Rightarrow \\ $$$$\begin{cases}{{r}\left(\mathrm{tan}\:\theta\mathrm{sin}\:\phi−\mathrm{cos}\:\phi\right)={p}}\\{{q}\left(\mathrm{tan}\:\phi\mathrm{sin}\:\theta−\mathrm{cos}\:\theta\right)={p}}\end{cases} \\ $$$$\mathrm{tan}\:\theta\mathrm{tan}\:\phi=\frac{{p}}{{r}}\mathrm{sec}\:\phi+\mathrm{1}=\frac{{p}}{{q}}\mathrm{sec}\:\theta+\mathrm{1} \\ $$$$\Rightarrow\:\:{r}\mathrm{cos}\:\phi={q}\mathrm{cos}\:\theta\:={x} \\ $$$$\left\{{otherwise}\right. \\ $$$$\:\:{A}=\left(\frac{{p}+{x}}{\mathrm{2}}\right)\left(\sqrt{{q}^{\mathrm{2}} −{x}^{\mathrm{2}} }+\sqrt{{r}^{\mathrm{2}} −{x}^{\mathrm{2}} }\right) \\ $$$${Now}\:\:\:\frac{{dA}}{{dx}}=\mathrm{0}\:\:\Rightarrow \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\left(\sqrt{{q}^{\mathrm{2}} −{x}^{\mathrm{2}} }+\sqrt{{r}^{\mathrm{2}} −{x}^{\mathrm{2}} }\right) \\ $$$$\:\:\:\:=\:\frac{{x}\left({p}+{x}\right)}{\mathrm{2}}\left[\frac{\mathrm{1}}{\:\sqrt{{q}^{\mathrm{2}} −{x}^{\mathrm{2}} }}+\frac{\mathrm{1}}{\:\sqrt{{r}^{\mathrm{2}} −{x}^{\mathrm{2}} }}\right] \\ $$$$\left({q}^{\mathrm{2}} −{x}^{\mathrm{2}} \right)\left({r}^{\mathrm{2}} −{x}^{\mathrm{2}} \right)={x}^{\mathrm{2}} \left({p}+{x}\right)^{\mathrm{2}} \\ $$$$\mathrm{2}{px}^{\mathrm{3}} +\left({p}^{\mathrm{2}} +{q}^{\mathrm{2}} +{r}^{\mathrm{2}} \right){x}^{\mathrm{2}} −{q}^{\mathrm{2}} {r}^{\mathrm{2}} =\mathrm{0} \\ $$$$\Rightarrow\:\frac{\mathrm{1}}{{x}^{\mathrm{3}} }−\left(\frac{{p}^{\mathrm{2}} +{q}^{\mathrm{2}} +{r}^{\mathrm{2}} }{{q}^{\mathrm{2}} {r}^{\mathrm{2}} }\right)\frac{\mathrm{1}}{{x}}−\frac{\mathrm{2}{p}}{{q}^{\mathrm{2}} {r}^{\mathrm{2}} }=\mathrm{0} \\ $$$${D}=\left\{\frac{{p}}{{q}^{\mathrm{2}} {r}^{\mathrm{2}} }\right\}^{\mathrm{2}} −\frac{\mathrm{1}}{\mathrm{27}}\left\{\frac{{p}^{\mathrm{2}} +{q}^{\mathrm{2}} +{r}^{\mathrm{2}} }{{q}^{\mathrm{2}} {r}^{\mathrm{2}} }\right\}^{\mathrm{3}} \\ $$$$\:{D}\left({q}^{\mathrm{2}} {r}^{\mathrm{2}} \right)^{\mathrm{3}} ={p}^{\mathrm{2}} {q}^{\mathrm{2}} {r}^{\mathrm{2}} −\left(\frac{{p}^{\mathrm{2}} +{q}^{\mathrm{2}} +{r}^{\mathrm{2}} }{\mathrm{3}}\right)^{\mathrm{3}} \\ $$$${Sir},\:{what}\:{can}\:{be}\:{said}\:{about}\:{the} \\ $$$${sign}\:{of}\:{Discriminant}\:{here}? \\ $$$$\left.\:\:\right\} \\ $$$${or}\:\:{r}\mathrm{sec}\:\theta={q}\mathrm{sec}\:\phi \\ $$$$\Rightarrow\:\sqrt{\mathrm{1}+\mathrm{sec}\:^{\mathrm{2}} \theta}\sqrt{\frac{{r}^{\mathrm{2}} }{{q}^{\mathrm{2}} }\mathrm{sec}\:^{\mathrm{2}} \theta−\mathrm{1}}=\frac{{p}}{{q}}\mathrm{sec}\:\theta+\mathrm{1} \\ $$$${let}\:\:\mathrm{sec}\:\theta={t} \\ $$$$\:\left(\mathrm{1}+{t}^{\mathrm{2}} \right)\left(\frac{{r}^{\mathrm{2}} {t}^{\mathrm{2}} }{{q}^{\mathrm{2}} }−\mathrm{1}\right)=\frac{{p}^{\mathrm{2}} {t}^{\mathrm{2}} }{{q}^{\mathrm{2}} }+\frac{\mathrm{2}{pt}}{{q}}+\mathrm{1} \\ $$$${its}\:{a}\:{biquadratic}… \\ $$$${similarly}\:{for}\:\mathrm{tan}\:\phi…. \\ $$$$…… \\ $$$${AB}=\mathrm{2}\sqrt{\left({q}\mathrm{cos}\:\theta+{p}\right)^{\mathrm{2}} +{q}^{\mathrm{2}} \mathrm{sin}\:^{\mathrm{2}} \theta} \\ $$$${BC}=\mathrm{2}\sqrt{\left({q}\mathrm{cos}\:\theta−{r}\mathrm{cos}\:\phi\right)^{\mathrm{2}} +\left({q}\mathrm{sin}\:\theta+{r}\mathrm{sin}\:\phi\right)^{\mathrm{2}} } \\ $$$${CA}=\mathrm{2}\sqrt{\left({r}\mathrm{cos}\:\phi−{p}\right)^{\mathrm{2}} +{r}^{\mathrm{2}} \mathrm{sin}\:^{\mathrm{2}} \phi} \\ $$$$. \\ $$
Commented by mr W last updated on 12/Feb/20

$${ingenious}\:{idea}! \\ $$$$\Delta_{{ABC}} =\mathrm{4}\Delta_{{shaded}} \\ $$
Commented by mr W last updated on 12/Feb/20
))=0 ⇒((sin α tan (α+β))/( (√(((q/p))^2 −sin^2 α))))=1 ...(i) similarly ⇒((sin β tan (α+β))/( (√(((r/p))^2 −sin^2 β))))=1 ...(ii) let (q/p)=δ>1, (r/p)=γ>1 ⇒((sin α)/( (√(δ^2 −sin^2 α))))=(1/(tan (α+β)))=(1/t) (1+t^2 )sin^2 α=δ^2 ⇒sin α=(δ/( (√(1+t^2 )))) ⇒tan α=(δ/( (√(1+t^2 −δ^2 )))) similarly ⇒sin β=(γ/( (√(1+t^2 )))) ⇒tan β=(γ/( (√(1+t^2 −γ^2 )))) t=tan (α+β)=((tan α+tan β)/(1−tan α tan β)) ⇒t=((δ(√(1+t^2 −γ^2 ))+γ(√(1+t^2 −δ^2 )))/( (√((1+t^2 −δ^2 )(1+t^2 −γ^2 )))−δγ)) c=2PQ=2(p cos α+(√(p^2 cos^2 α+q^2 −p^2 ))) b=2PR=2(p cos β+(√(p^2 cos^2 β+r^2 −p^2 ))) a=2QR=2(PQ×sin α+PR×sin β)](https://www.tinkutara.com/question/Q81416.png)
$${q}^{\mathrm{2}} ={p}^{\mathrm{2}} +{PQ}^{\mathrm{2}} −\mathrm{2}{p}×{PQ}\:\mathrm{cos}\:\alpha \\ $$$${PQ}^{\mathrm{2}} −\mathrm{2}{p}\mathrm{cos}\:\alpha×{PQ}−\left({q}^{\mathrm{2}} −{p}^{\mathrm{2}} \right)=\mathrm{0} \\ $$$${PQ}={p}\:\mathrm{cos}\:\alpha+\sqrt{{p}^{\mathrm{2}} \mathrm{cos}^{\mathrm{2}} \:\alpha+{q}^{\mathrm{2}} −{p}^{\mathrm{2}} } \\ $$$${similarly} \\ $$$${PR}={p}\:\mathrm{cos}\:\beta+\sqrt{{p}^{\mathrm{2}} \mathrm{cos}^{\mathrm{2}} \:\beta+{r}^{\mathrm{2}} −{p}^{\mathrm{2}} } \\ $$$${A}=\mathrm{2}\Delta_{{PQR}} =\mathrm{sin}\:\left(\alpha+\beta\right)\left({p}\:\mathrm{cos}\:\alpha+\sqrt{{p}^{\mathrm{2}} \mathrm{cos}^{\mathrm{2}} \:\alpha+{q}^{\mathrm{2}} −{p}^{\mathrm{2}} }\right)\left({p}\:\mathrm{cos}\:\beta+\sqrt{{p}^{\mathrm{2}} \mathrm{cos}^{\mathrm{2}} \:\beta+{q}^{\mathrm{2}} −{r}^{\mathrm{2}} }\right) \\ $$$$\frac{\partial{A}}{\partial\alpha}=\left[\mathrm{cos}\:\left(\alpha+\beta\right)\left({p}\:\mathrm{cos}\:\alpha+\sqrt{{p}^{\mathrm{2}} \mathrm{cos}^{\mathrm{2}} \:\alpha+{q}^{\mathrm{2}} −{p}^{\mathrm{2}} }\right)−{p}\:\mathrm{sin}\:\left(\alpha+\beta\right)\mathrm{sin}\:\alpha\left(\frac{{p}\mathrm{cos}\:\alpha+\sqrt{{p}^{\mathrm{2}} \mathrm{cos}^{\mathrm{2}} \:\alpha+{q}^{\mathrm{2}} −{p}^{\mathrm{2}} }}{\:\sqrt{{p}^{\mathrm{2}} \mathrm{cos}^{\mathrm{2}} \:\alpha+{q}^{\mathrm{2}} −{p}^{\mathrm{2}} }}\right)\right]\left({p}\:\mathrm{cos}\:\beta+\sqrt{{p}^{\mathrm{2}} \mathrm{cos}^{\mathrm{2}} \:\beta+{q}^{\mathrm{2}} −{r}^{\mathrm{2}} }\right)=\mathrm{0} \\ $$$$\Rightarrow\frac{\mathrm{sin}\:\alpha\:\mathrm{tan}\:\left(\alpha+\beta\right)}{\:\sqrt{\left(\frac{{q}}{{p}}\right)^{\mathrm{2}} −\mathrm{sin}^{\mathrm{2}} \:\alpha}}=\mathrm{1}\:\:\:…\left({i}\right) \\ $$$${similarly} \\ $$$$\Rightarrow\frac{\mathrm{sin}\:\beta\:\mathrm{tan}\:\left(\alpha+\beta\right)}{\:\sqrt{\left(\frac{{r}}{{p}}\right)^{\mathrm{2}} −\mathrm{sin}^{\mathrm{2}} \:\beta}}=\mathrm{1}\:\:\:…\left({ii}\right) \\ $$$${let}\:\frac{{q}}{{p}}=\delta>\mathrm{1},\:\frac{{r}}{{p}}=\gamma>\mathrm{1} \\ $$$$\Rightarrow\frac{\mathrm{sin}\:\alpha}{\:\sqrt{\delta^{\mathrm{2}} −\mathrm{sin}^{\mathrm{2}} \:\alpha}}=\frac{\mathrm{1}}{\mathrm{tan}\:\left(\alpha+\beta\right)}=\frac{\mathrm{1}}{{t}} \\ $$$$\left(\mathrm{1}+{t}^{\mathrm{2}} \right)\mathrm{sin}^{\mathrm{2}} \:\alpha=\delta^{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{sin}\:\alpha=\frac{\delta}{\:\sqrt{\mathrm{1}+{t}^{\mathrm{2}} }}\:\Rightarrow\mathrm{tan}\:\alpha=\frac{\delta}{\:\sqrt{\mathrm{1}+{t}^{\mathrm{2}} −\delta^{\mathrm{2}} }} \\ $$$${similarly} \\ $$$$\Rightarrow\mathrm{sin}\:\beta=\frac{\gamma}{\:\sqrt{\mathrm{1}+{t}^{\mathrm{2}} }}\:\Rightarrow\mathrm{tan}\:\beta=\frac{\gamma}{\:\sqrt{\mathrm{1}+{t}^{\mathrm{2}} −\gamma^{\mathrm{2}} }} \\ $$$${t}=\mathrm{tan}\:\left(\alpha+\beta\right)=\frac{\mathrm{tan}\:\alpha+\mathrm{tan}\:\beta}{\mathrm{1}−\mathrm{tan}\:\alpha\:\mathrm{tan}\:\beta} \\ $$$$\Rightarrow{t}=\frac{\delta\sqrt{\mathrm{1}+{t}^{\mathrm{2}} −\gamma^{\mathrm{2}} }+\gamma\sqrt{\mathrm{1}+{t}^{\mathrm{2}} −\delta^{\mathrm{2}} }}{\:\sqrt{\left(\mathrm{1}+{t}^{\mathrm{2}} −\delta^{\mathrm{2}} \right)\left(\mathrm{1}+{t}^{\mathrm{2}} −\gamma^{\mathrm{2}} \right)}−\delta\gamma} \\ $$$$ \\ $$$${c}=\mathrm{2}{PQ}=\mathrm{2}\left({p}\:\mathrm{cos}\:\alpha+\sqrt{{p}^{\mathrm{2}} \mathrm{cos}^{\mathrm{2}} \:\alpha+{q}^{\mathrm{2}} −{p}^{\mathrm{2}} }\right) \\ $$$${b}=\mathrm{2}{PR}=\mathrm{2}\left({p}\:\mathrm{cos}\:\beta+\sqrt{{p}^{\mathrm{2}} \mathrm{cos}^{\mathrm{2}} \:\beta+{r}^{\mathrm{2}} −{p}^{\mathrm{2}} }\right) \\ $$$${a}=\mathrm{2}{QR}=\mathrm{2}\left({PQ}×\mathrm{sin}\:\alpha+{PR}×\mathrm{sin}\:\beta\right) \\ $$
Commented by mr W last updated on 12/Feb/20

$${then}\:{we}\:{can}\:{apply}\:{the}\:{result}\:{from} \\ $$$${Q}\mathrm{61861}. \\ $$
Commented by ajfour last updated on 12/Feb/20

$${yes}\:{Sir},\:{i}\:{viewed}\:{it},\:{thanks}, \\ $$$${twas}\:{good}\:{reviewing}\:{it}.. \\ $$
Commented by mr W last updated on 13/Feb/20

$${you}\:{have}\:{solved}\:{the}\:{question}\:{perfectly} \\ $$$${sir}!\:{we}\:{get}\:{a}\:{cubic}\:{final}\:{equation}\:{which} \\ $$$${can}\:{be}\:{solved}. \\ $$
Answered by ajfour last updated on 12/Feb/20

$${h}^{\mathrm{2}} +{k}^{\mathrm{2}} ={p}^{\mathrm{2}} \\ $$$$\left({h}−\left({b}−{a}\right)\right)^{\mathrm{2}} +\left({k}−{c}\right)^{\mathrm{2}} ={r}^{\mathrm{2}} \:\:\:..\left({i}\right) \\ $$$$\left({h}−\left({b}+{a}\right)\right)^{\mathrm{2}} +\left({k}−{c}\right)^{\mathrm{2}} ={q}^{\mathrm{2}} \:\:\:..\left({ii}\right) \\ $$$${subtracting} \\ $$$$\mathrm{4}{ah}={r}^{\mathrm{2}} −{q}^{\mathrm{2}} +\mathrm{4}{ab}\:\:\:\:\:….\left({I}\right) \\ $$$${Rewriting}\:\left({i}\right)\&\left({ii}\right) \\ $$$$\Rightarrow\:−\mathrm{2}{h}\left({b}−{a}\right)+\left({b}−{a}\right)^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:−\mathrm{2}{kc}+{c}^{\mathrm{2}} \:={r}^{\mathrm{2}} −{p}^{\mathrm{2}} \:\:\:\:\:\:\:….\left({iA}\right) \\ $$$$\&\:\:\:\:−\mathrm{2}{h}\left({b}+{a}\right)+\left({b}+{a}\right)^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:−\mathrm{2}{kc}+{c}^{\mathrm{2}} ={q}^{\mathrm{2}} −{p}^{\mathrm{2}} \:\:\:\:\:\:\:\:…\left({iiA}\right) \\ $$$${adding} \\ $$$$−\mathrm{4}{bh}−\mathrm{4}{kc}+\mathrm{2}{c}^{\mathrm{2}} +\mathrm{2}\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:={q}^{\mathrm{2}} +{r}^{\mathrm{2}} −\mathrm{2}{p}^{\mathrm{2}} \\ $$$$\:\:\:{k}=\frac{\mathrm{4}{bh}−\mathrm{2}{c}^{\mathrm{2}} −\mathrm{2}\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right)+{q}^{\mathrm{2}} +{r}^{\mathrm{2}} −\mathrm{2}{p}^{\mathrm{2}} }{\mathrm{4}{c}} \\ $$$$\:{k}\:=\frac{{b}\left\{{r}^{\mathrm{2}} −{q}^{\mathrm{2}} +\mathrm{4}{ab}\right\}−\mathrm{2}{ac}^{\mathrm{2}} −\mathrm{2}{a}\left({a}^{\mathrm{2}} +{b}^{\mathrm{2}} \right)+{a}\left\{{q}^{\mathrm{2}} +{r}^{\mathrm{2}} −\mathrm{2}{p}^{\mathrm{2}} \right\}}{\mathrm{4}{ac}} \\ $$$${Now}\:\:\:{h}^{\mathrm{2}} +{k}^{\mathrm{2}} ={p}^{\mathrm{2}} \\ $$$${we}\:{get}\:{a},{b},{c}\:{related}. \\ $$$${say}\:\:{b}={f}\left({a},{c}\right) \\ $$$${A}=\mathrm{4}{ac} \\ $$$$\frac{\partial{A}}{\partial{a}}=\mathrm{0}\:,\:\:\frac{\partial{A}}{\partial{c}}=\mathrm{0}\:\:\: \\ $$$${should}\:{get}\:{us}\:\:\:{a},\:{c},\:{f}\left({a},{c}\right)={b} \\ $$$${Now}\:\:{AB}=\sqrt{\left(\mathrm{2}{b}+\mathrm{2}{a}\right)^{\mathrm{2}} +\mathrm{4}{c}^{\mathrm{2}} } \\ $$$$\:\:\:\:{BC}=\mathrm{4}{a}\:,\:{CA}=\sqrt{\left(\mathrm{2}{b}−\mathrm{2}{a}\right)^{\mathrm{2}} +\mathrm{4}{c}^{\mathrm{2}} } \\ $$$$……. \\ $$
Commented by mr W last updated on 12/Feb/20

$${it}'{s}\:{great}\:{sir}!\:{thanks}! \\ $$$$ \\ $$$${we}\:{get}\:{a}\:{relation}\:\left({condition}\right)\:{for}\:{a},{b},{c}, \\ $$$${say}\:{F}\left({a},{b},{c}\right)=\mathrm{0} \\ $$$${to}\:{get}\:{maximum}\:{of}\:{A}=\mathrm{4}{ac},\:{we}\:{can} \\ $$$${use}\:{P}=\mathrm{4}{ac}+\lambda{F}\left({a},{b},{c}\right)\:{and} \\ $$$$\frac{\partial{P}}{\partial{a}}=\mathrm{4}{c}+\lambda\frac{\partial{F}\left({a},{b},{c}\right)}{\partial{a}}=\mathrm{0} \\ $$$$\frac{\partial{P}}{\partial{b}}=\lambda\frac{\partial{F}\left({a},{b},{c}\right)}{\partial{b}}=\mathrm{0} \\ $$$$\frac{\partial{P}}{\partial{c}}=\mathrm{4}{a}+\lambda\frac{\partial{F}\left({a},{b},{c}\right)}{\partial{c}}=\mathrm{0} \\ $$$$\frac{\partial{P}}{\partial\lambda}={F}\left({a},{b},{c}\right)=\mathrm{0} \\ $$$$ \\ $$$$\Rightarrow{F}\left({a},{b},{c}\right)=\mathrm{0}\:\:\:\:…\left({I}\right) \\ $$$$\Rightarrow\frac{\partial{F}\left({a},{b},{c}\right)}{\partial{b}}=\mathrm{0}\:\:…\left({II}\right) \\ $$$$\Rightarrow{a}\frac{\partial{F}\left({a},{b},{c}\right)}{\partial{a}}={c}\frac{\partial{F}\left({a},{b},{c}\right)}{\partial{c}}\:\:\:…\left({III}\right) \\ $$$${we}\:{get}\:{a},{b},{c}\:{from}\:{these}\:{three}\:{eqn}. \\ $$
