Question-81421

Question Number 81421 by ajfour last updated on 12/Feb/20

Commented by ajfour last updated on 12/Feb/20

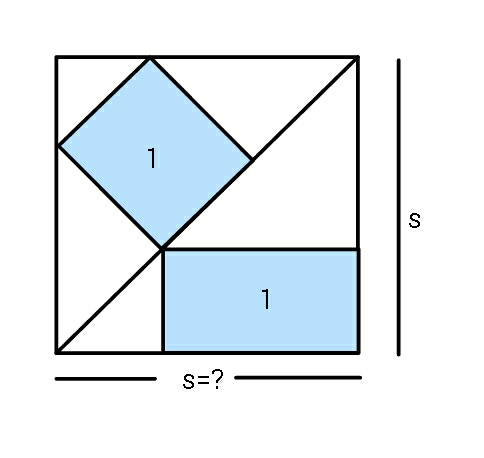
I f b o t h r e c t a n g l e s h a v e u n i t

a r e a s, f i n d t h e s i d e l e n g t h o f

t h e o u t e r s q u a r e .

Answered by ajfour last updated on 12/Feb/20

(s - x) x = 1

(x \sqrt{2}) {s \sqrt{2} - 2 \sqrt{2} x} = 1

e q u a t i n g

2 s - 4 x = s - x

\Rightarrow x = s / 3

\Rightarrow (\frac{2 s}{3}) (\frac{s}{3}) = 1

\Rightarrow s = \frac{3 \sqrt{2}}{2} .

Facebook Tweet Pin