Question Number 81435 by naka3546 last updated on 13/Feb/20
Commented by naka3546 last updated on 13/Feb/20
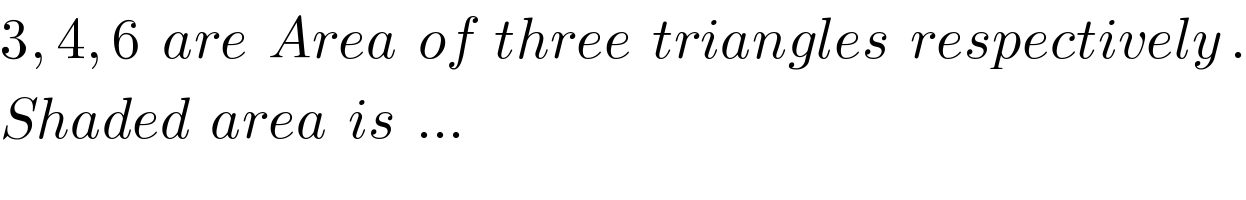
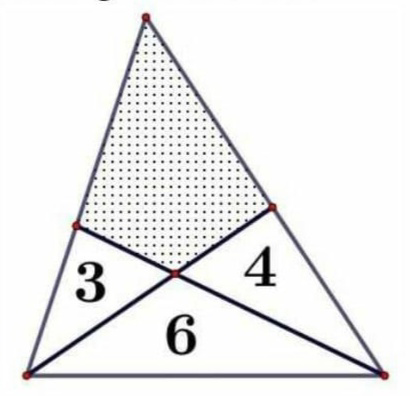
$$\mathrm{3},\:\mathrm{4},\:\mathrm{6}\:\:{are}\:\:{Area}\:\:{of}\:\:{three}\:\:{triangles}\:\:{respectively}\:. \\ $$$${Shaded}\:\:{area}\:\:{is}\:\:…\: \\ $$
Commented by john santu last updated on 13/Feb/20

$$\frac{\mathrm{x}+\mathrm{y}+\mathrm{4}}{\mathrm{3}+\mathrm{6}}\:=\:\frac{\mathrm{b}_{\mathrm{1}} }{\mathrm{b}_{\mathrm{2}} }\:\Rightarrow\:\frac{\mathrm{x}+\mathrm{y}+\mathrm{4}}{\mathrm{9}}\:=\frac{\mathrm{b}_{\mathrm{1}} }{\mathrm{b}_{\mathrm{2}} }\:=\frac{\mathrm{x}}{\mathrm{3}}\left(\mathrm{i}\right) \\ $$$$\frac{\mathrm{x}+\mathrm{y}+\mathrm{3}}{\mathrm{6}+\mathrm{4}}\:=\:\frac{\mathrm{b}_{\mathrm{3}} }{\mathrm{b}_{\mathrm{4}} }\:=\:\frac{\mathrm{y}}{\mathrm{4}}\left(\mathrm{ii}\right) \\ $$$$\left(\mathrm{i}\right)\:\mathrm{3x}+\mathrm{3y}+\mathrm{12}\:=\:\mathrm{9x}\:\Rightarrow\mathrm{6x}−\mathrm{3y}=\mathrm{12} \\ $$$$\mathrm{2x}−\mathrm{y}=\mathrm{4} \\ $$$$\left(\mathrm{ii}\right)\:\mathrm{4x}+\mathrm{4y}+\mathrm{12}\:=\:\mathrm{10y}\:\Rightarrow\mathrm{4x}−\mathrm{6y}=−\mathrm{12} \\ $$$$\mathrm{2x}−\mathrm{3y}=−\mathrm{6} \\ $$$$\mathrm{elimination}\:\left(\mathrm{i}\right)\:\wedge\left(\mathrm{ii}\right) \\ $$$$\Rightarrow\mathrm{y}\:=\:\mathrm{5}\:\wedge\:\mathrm{x}\:=\:\frac{\mathrm{9}}{\mathrm{2}} \\ $$$$\mathrm{shaded}\:\mathrm{area}\:=\:\mathrm{x}+\mathrm{y}\:=\:\frac{\mathrm{19}}{\mathrm{2}} \\ $$$$ \\ $$
Commented by naka3546 last updated on 13/Feb/20

$$\mathrm{9}.\mathrm{5}\:\:,\:\:{sir}\:? \\ $$
Commented by mr W last updated on 13/Feb/20

$$\mathrm{9}.\mathrm{5}\:{is}\:{correct}. \\ $$
Commented by john santu last updated on 13/Feb/20

$$\mathrm{post}\:\mathrm{you}\:\mathrm{work}? \\ $$
Commented by john santu last updated on 13/Feb/20
$$\mathrm{yes}\:\mathrm{right},\:\mathrm{i}\:\mathrm{misscalculated}\:\mathrm{the} \\ $$$$\mathrm{second}\:\mathrm{equation} \\ $$
Answered by john santu last updated on 13/Feb/20

Answered by mr W last updated on 13/Feb/20
Commented by mr W last updated on 13/Feb/20
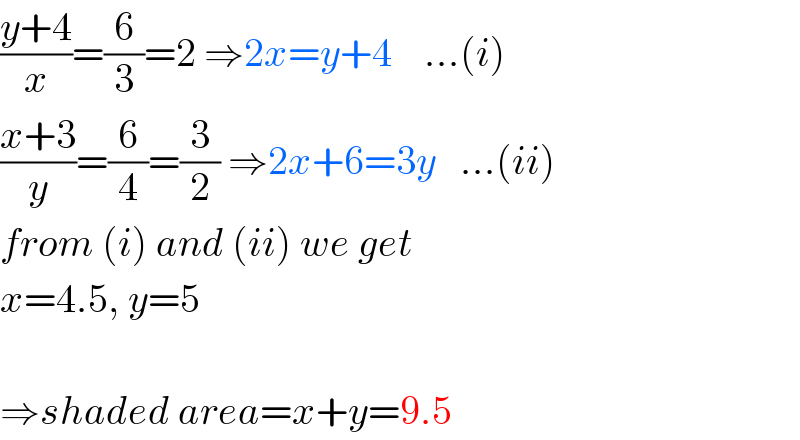
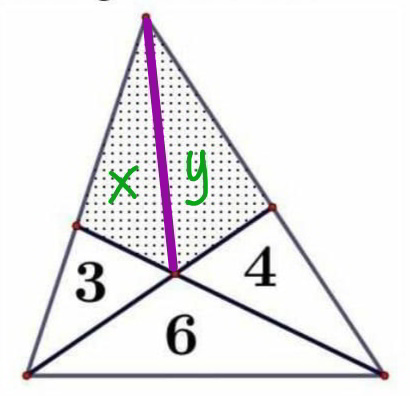
$$\frac{{y}+\mathrm{4}}{{x}}=\frac{\mathrm{6}}{\mathrm{3}}=\mathrm{2}\:\Rightarrow\mathrm{2}{x}={y}+\mathrm{4}\:\:\:\:…\left({i}\right) \\ $$$$\frac{{x}+\mathrm{3}}{{y}}=\frac{\mathrm{6}}{\mathrm{4}}=\frac{\mathrm{3}}{\mathrm{2}}\:\Rightarrow\mathrm{2}{x}+\mathrm{6}=\mathrm{3}{y}\:\:\:…\left({ii}\right) \\ $$$${from}\:\left({i}\right)\:{and}\:\left({ii}\right)\:{we}\:{get} \\ $$$${x}=\mathrm{4}.\mathrm{5},\:{y}=\mathrm{5} \\ $$$$ \\ $$$$\Rightarrow{shaded}\:{area}={x}+{y}=\mathrm{9}.\mathrm{5} \\ $$
Commented by john santu last updated on 13/Feb/20
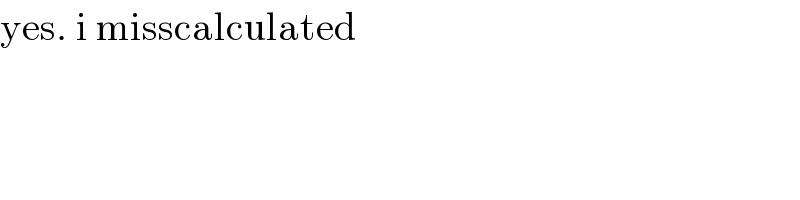
$$\mathrm{yes}.\:\mathrm{i}\:\mathrm{misscalculated} \\ $$
