Question Number 81506 by Power last updated on 13/Feb/20
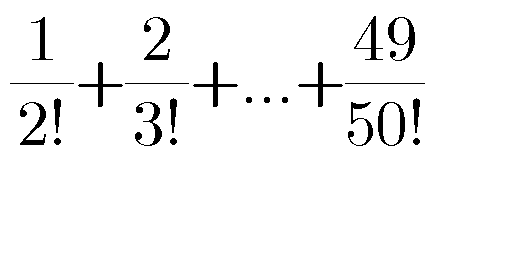
Commented by Power last updated on 13/Feb/20
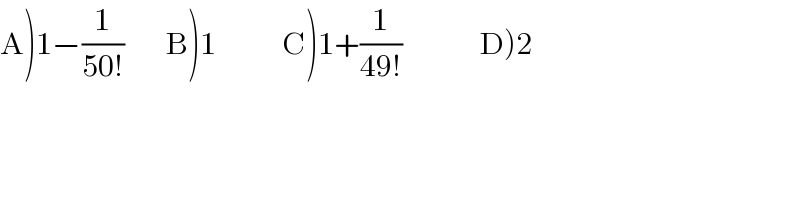
$$\left.\mathrm{A}\left.\right)\left.\mathrm{1}\left.−\frac{\mathrm{1}}{\mathrm{50}!}\:\:\:\:\:\:\:\mathrm{B}\right)\mathrm{1}\:\:\:\:\:\:\:\:\:\:\:\mathrm{C}\right)\mathrm{1}+\frac{\mathrm{1}}{\mathrm{49}!}\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{D}\right)\mathrm{2} \\ $$
Commented by mr W last updated on 13/Feb/20
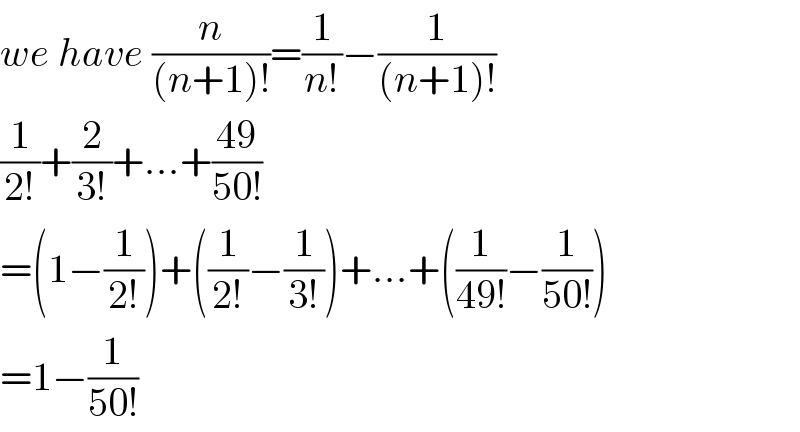
$${we}\:{have}\:\frac{{n}}{\left({n}+\mathrm{1}\right)!}=\frac{\mathrm{1}}{{n}!}−\frac{\mathrm{1}}{\left({n}+\mathrm{1}\right)!} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}!}+\frac{\mathrm{2}}{\mathrm{3}!}+…+\frac{\mathrm{49}}{\mathrm{50}!} \\ $$$$=\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{2}!}\right)+\left(\frac{\mathrm{1}}{\mathrm{2}!}−\frac{\mathrm{1}}{\mathrm{3}!}\right)+…+\left(\frac{\mathrm{1}}{\mathrm{49}!}−\frac{\mathrm{1}}{\mathrm{50}!}\right) \\ $$$$=\mathrm{1}−\frac{\mathrm{1}}{\mathrm{50}!} \\ $$
Commented by Power last updated on 13/Feb/20

$$\mathrm{thanks} \\ $$
Commented by Power last updated on 13/Feb/20

$$\mathrm{thanks} \\ $$
