Question Number 81507 by Power last updated on 13/Feb/20

Commented by mr W last updated on 13/Feb/20
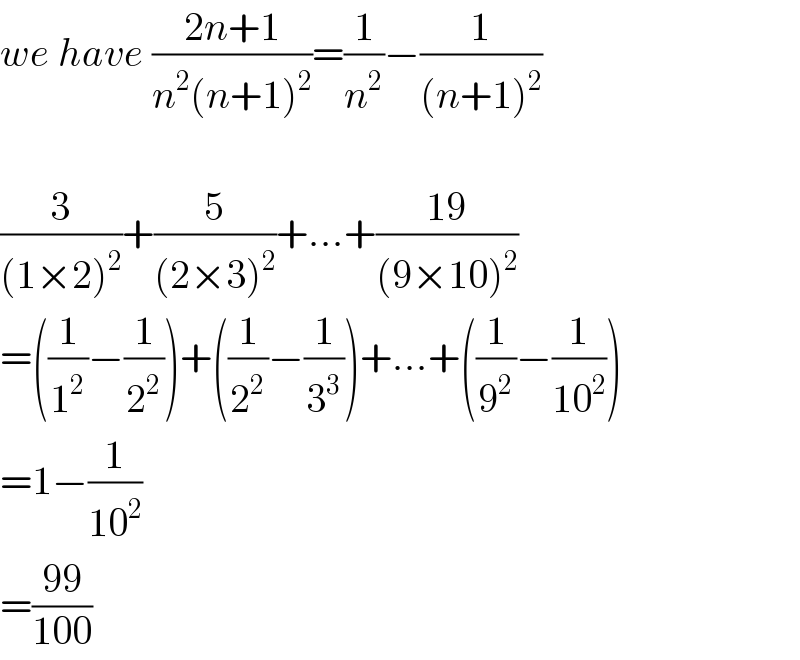
$${we}\:{have}\:\frac{\mathrm{2}{n}+\mathrm{1}}{{n}^{\mathrm{2}} \left({n}+\mathrm{1}\right)^{\mathrm{2}} }=\frac{\mathrm{1}}{{n}^{\mathrm{2}} }−\frac{\mathrm{1}}{\left({n}+\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$ \\ $$$$\frac{\mathrm{3}}{\left(\mathrm{1}×\mathrm{2}\right)^{\mathrm{2}} }+\frac{\mathrm{5}}{\left(\mathrm{2}×\mathrm{3}\right)^{\mathrm{2}} }+…+\frac{\mathrm{19}}{\left(\mathrm{9}×\mathrm{10}\right)^{\mathrm{2}} } \\ $$$$=\left(\frac{\mathrm{1}}{\mathrm{1}^{\mathrm{2}} }−\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{2}} }\right)+\left(\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{2}} }−\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{3}} }\right)+…+\left(\frac{\mathrm{1}}{\mathrm{9}^{\mathrm{2}} }−\frac{\mathrm{1}}{\mathrm{10}^{\mathrm{2}} }\right) \\ $$$$=\mathrm{1}−\frac{\mathrm{1}}{\mathrm{10}^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{99}}{\mathrm{100}} \\ $$
