Question Number 81562 by ajfour last updated on 14/Feb/20

Commented by ajfour last updated on 14/Feb/20

$${If}\:{pulled}\:{slightly}\:{more}, \\ $$$${hemisphere}\:{slips},\:{find}\:{tension} \\ $$$$\:{in}\:{shown}\:{equilibrium}\:{state}. \\ $$
Commented by mr W last updated on 14/Feb/20
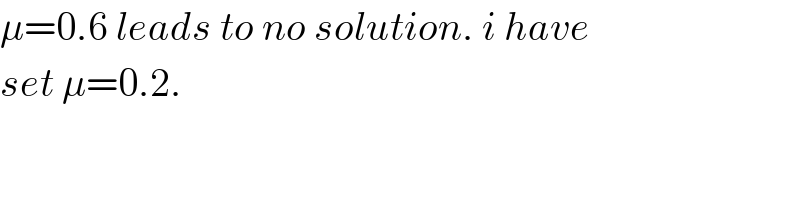
$$\mu=\mathrm{0}.\mathrm{6}\:{leads}\:{to}\:{no}\:{solution}.\:{i}\:{have} \\ $$$${set}\:\mu=\mathrm{0}.\mathrm{2}. \\ $$
Answered by mr W last updated on 14/Feb/20

Commented by mr W last updated on 15/Feb/20
![l sin ϕ+R sin θ+R=h 2 sin ϕ+sin θ+1=3 ⇒2 sin ϕ+sin θ=2 ...(i) N+T sin ϕ=mg ...(ii) T cos ϕ=f=μN ...(iii) T cos ϕ (R sin θ+R)+T sin ϕ R cos θ=mg e sin θ T [sin (ϕ+θ)+cos ϕ]=mg e sin θ ...(iv) ⇒sin θ=2(1−sin ϕ) T cos ϕ=μ(mg−T sin ϕ) T(cos ϕ+μ sin ϕ)=μmg ⇒T=((μmg)/(cos ϕ+μ sin ϕ)) ((μmg)/(cos ϕ+μ sin ϕ))[sin (ϕ+θ)+cos ϕ]=mg e sin θ ((μ{sin (ϕ+θ)+cos ϕ})/(cos ϕ+μ sin ϕ))=2e(1−sin ϕ) e=((3R)/8)=(3/8) ⇒((sin (ϕ+θ)+cos ϕ)/((cos ϕ+μ sin ϕ)(1−sin ϕ)))=(3/(4μ)) with θ=sin^(−1) [2(1−sin ϕ)] with μ=0.6 there is no solution possible. let′s say μ=0.2, we get ϕ≈30.3375° ⇒T=155.59 N ===================== μ=((3 cos ϕ(1−sin ϕ))/(4sin (ϕ+θ)+4cos ϕ+3 sin^2 ϕ−3sin ϕ)) ϕ→30° θ→90° μ<(3/(16−(√3)))≈0.21](https://www.tinkutara.com/question/Q81576.png)
$${l}\:\mathrm{sin}\:\varphi+{R}\:\mathrm{sin}\:\theta+{R}={h} \\ $$$$\mathrm{2}\:\mathrm{sin}\:\varphi+\mathrm{sin}\:\theta+\mathrm{1}=\mathrm{3} \\ $$$$\Rightarrow\mathrm{2}\:\mathrm{sin}\:\varphi+\mathrm{sin}\:\theta=\mathrm{2}\:\:\:\:…\left({i}\right) \\ $$$${N}+{T}\:\mathrm{sin}\:\varphi={mg}\:\:\:…\left({ii}\right) \\ $$$${T}\:\mathrm{cos}\:\varphi={f}=\mu{N}\:\:\:…\left({iii}\right) \\ $$$${T}\:\mathrm{cos}\:\varphi\:\left({R}\:\mathrm{sin}\:\theta+{R}\right)+{T}\:\mathrm{sin}\:\varphi\:{R}\:\mathrm{cos}\:\theta={mg}\:{e}\:\mathrm{sin}\:\theta \\ $$$${T}\:\left[\mathrm{sin}\:\left(\varphi+\theta\right)+\mathrm{cos}\:\varphi\right]={mg}\:{e}\:\mathrm{sin}\:\theta\:\:\:…\left({iv}\right) \\ $$$$ \\ $$$$\Rightarrow\mathrm{sin}\:\theta=\mathrm{2}\left(\mathrm{1}−\mathrm{sin}\:\varphi\right) \\ $$$${T}\:\mathrm{cos}\:\varphi=\mu\left({mg}−{T}\:\mathrm{sin}\:\varphi\right) \\ $$$${T}\left(\mathrm{cos}\:\varphi+\mu\:\mathrm{sin}\:\varphi\right)=\mu{mg} \\ $$$$\Rightarrow{T}=\frac{\mu{mg}}{\mathrm{cos}\:\varphi+\mu\:\mathrm{sin}\:\varphi} \\ $$$$\frac{\mu{mg}}{\mathrm{cos}\:\varphi+\mu\:\mathrm{sin}\:\varphi}\left[\mathrm{sin}\:\left(\varphi+\theta\right)+\mathrm{cos}\:\varphi\right]={mg}\:{e}\:\mathrm{sin}\:\theta \\ $$$$\frac{\mu\left\{\mathrm{sin}\:\left(\varphi+\theta\right)+\mathrm{cos}\:\varphi\right\}}{\mathrm{cos}\:\varphi+\mu\:\mathrm{sin}\:\varphi}=\mathrm{2}{e}\left(\mathrm{1}−\mathrm{sin}\:\varphi\right) \\ $$$${e}=\frac{\mathrm{3}{R}}{\mathrm{8}}=\frac{\mathrm{3}}{\mathrm{8}} \\ $$$$\Rightarrow\frac{\mathrm{sin}\:\left(\varphi+\theta\right)+\mathrm{cos}\:\varphi}{\left(\mathrm{cos}\:\varphi+\mu\:\mathrm{sin}\:\varphi\right)\left(\mathrm{1}−\mathrm{sin}\:\varphi\right)}=\frac{\mathrm{3}}{\mathrm{4}\mu} \\ $$$${with}\:\theta=\mathrm{sin}^{−\mathrm{1}} \left[\mathrm{2}\left(\mathrm{1}−\mathrm{sin}\:\varphi\right)\right] \\ $$$$ \\ $$$${with}\:\mu=\mathrm{0}.\mathrm{6}\:{there}\:{is}\:{no}\:{solution}\:{possible}. \\ $$$$ \\ $$$${let}'{s}\:{say}\:\mu=\mathrm{0}.\mathrm{2},\:{we}\:{get} \\ $$$$\varphi\approx\mathrm{30}.\mathrm{3375}° \\ $$$$\Rightarrow{T}=\mathrm{155}.\mathrm{59}\:{N} \\ $$$$ \\ $$$$===================== \\ $$$$\mu=\frac{\mathrm{3}\:\mathrm{cos}\:\varphi\left(\mathrm{1}−\mathrm{sin}\:\varphi\right)}{\mathrm{4sin}\:\left(\varphi+\theta\right)+\mathrm{4cos}\:\varphi+\mathrm{3}\:\mathrm{sin}^{\mathrm{2}} \:\varphi−\mathrm{3sin}\:\varphi} \\ $$$$\varphi\rightarrow\mathrm{30}° \\ $$$$\theta\rightarrow\mathrm{90}° \\ $$$$\mu<\frac{\mathrm{3}}{\mathrm{16}−\sqrt{\mathrm{3}}}\approx\mathrm{0}.\mathrm{21} \\ $$
Commented by ajfour last updated on 15/Feb/20

$${You}\:{have}\:{solved}\:{it}\:{in}\:{a}\:{very} \\ $$$${lucid}\:{way}\:{sir}!\:{I}\:{see}\:{it}\:{now}, \\ $$$${thanks}. \\ $$$$\left({useless}\:{trying}.\:{The}\:{way}\:{you}\right. \\ $$$${solved}\:{it}\:{Sir},\:{is}\:{satisfactory} \\ $$$$\left.{enough}!\right) \\ $$
