Question-81610

Question Number 81610 by TawaTawa last updated on 14/Feb/20

Answered by MJS last updated on 14/Feb/20

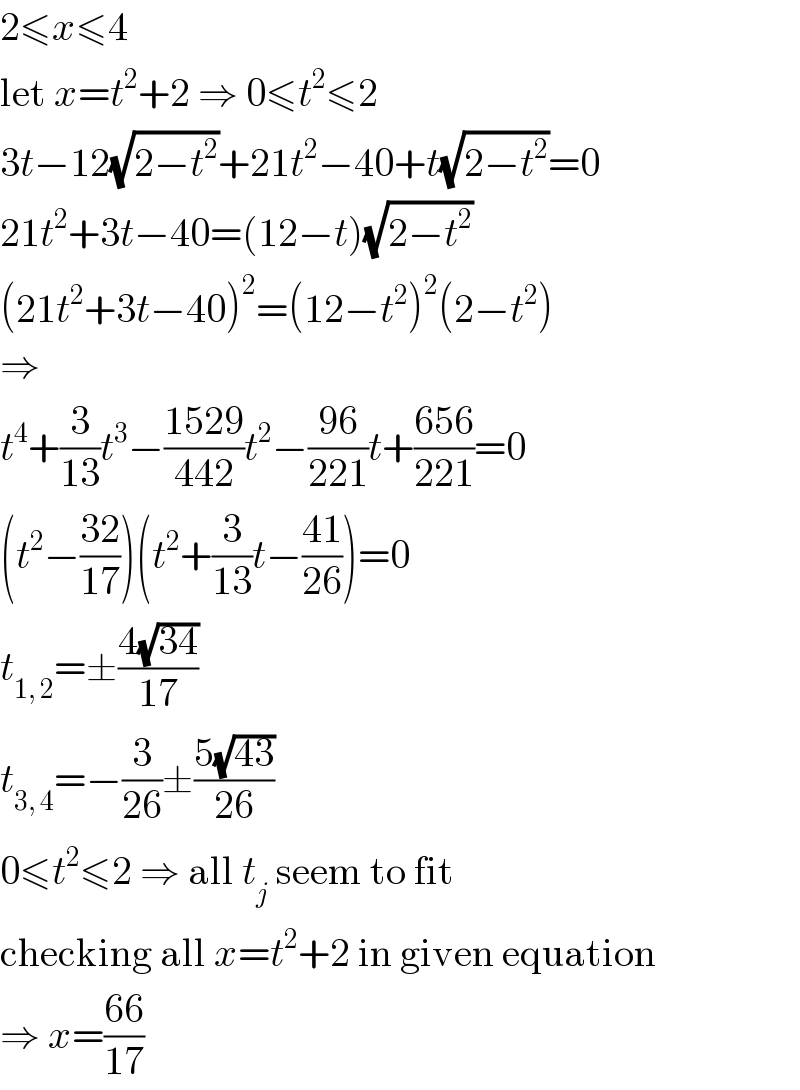
2≤x≤4 let x=t^2 +2 ⇒ 0≤t^2 ≤2 3t−12(√(2−t^2 ))+21t^2 −40+t(√(2−t^2 ))=0 21t^2 +3t−40=(12−t)(√(2−t^2 )) (21t^2 +3t−40)^2 =(12−t^2 )^2 (2−t^2 ) ⇒ t^4 +(3/(13))t^3 −((1529)/(442))t^2 −((96)/(221))t+((656)/(221))=0 (t^2 −((32)/(17)))(t^2 +(3/(13))t−((41)/(26)))=0 t_(1, 2) =±((4(√(34)))/(17)) t_(3, 4) =−(3/(26))±((5(√(43)))/(26)) 0≤t^2 ≤2 ⇒ all t_j seem to fit checking all x=t^2 +2 in given equation ⇒ x=((66)/(17))

$$\mathrm{2}\leqslant{x}\leqslant\mathrm{4} \\ $$$$\mathrm{let}\:{x}={t}^{\mathrm{2}} +\mathrm{2}\:\Rightarrow\:\mathrm{0}\leqslant{t}^{\mathrm{2}} \leqslant\mathrm{2} \\ $$$$\mathrm{3}{t}−\mathrm{12}\sqrt{\mathrm{2}−{t}^{\mathrm{2}} }+\mathrm{21}{t}^{\mathrm{2}} −\mathrm{40}+{t}\sqrt{\mathrm{2}−{t}^{\mathrm{2}} }=\mathrm{0} \\ $$$$\mathrm{21}{t}^{\mathrm{2}} +\mathrm{3}{t}−\mathrm{40}=\left(\mathrm{12}−{t}\right)\sqrt{\mathrm{2}−{t}^{\mathrm{2}} } \\ $$$$\left(\mathrm{21}{t}^{\mathrm{2}} +\mathrm{3}{t}−\mathrm{40}\right)^{\mathrm{2}} =\left(\mathrm{12}−{t}^{\mathrm{2}} \right)^{\mathrm{2}} \left(\mathrm{2}−{t}^{\mathrm{2}} \right) \\ $$$$\Rightarrow \\ $$$${t}^{\mathrm{4}} +\frac{\mathrm{3}}{\mathrm{13}}{t}^{\mathrm{3}} −\frac{\mathrm{1529}}{\mathrm{442}}{t}^{\mathrm{2}} −\frac{\mathrm{96}}{\mathrm{221}}{t}+\frac{\mathrm{656}}{\mathrm{221}}=\mathrm{0} \\ $$$$\left({t}^{\mathrm{2}} −\frac{\mathrm{32}}{\mathrm{17}}\right)\left({t}^{\mathrm{2}} +\frac{\mathrm{3}}{\mathrm{13}}{t}−\frac{\mathrm{41}}{\mathrm{26}}\right)=\mathrm{0} \\ $$$${t}_{\mathrm{1},\:\mathrm{2}} =\pm\frac{\mathrm{4}\sqrt{\mathrm{34}}}{\mathrm{17}} \\ $$$${t}_{\mathrm{3},\:\mathrm{4}} =−\frac{\mathrm{3}}{\mathrm{26}}\pm\frac{\mathrm{5}\sqrt{\mathrm{43}}}{\mathrm{26}} \\ $$$$\mathrm{0}\leqslant{t}^{\mathrm{2}} \leqslant\mathrm{2}\:\Rightarrow\:\mathrm{all}\:{t}_{{j}} \:\mathrm{seem}\:\mathrm{to}\:\mathrm{fit} \\ $$$$\mathrm{checking}\:\mathrm{all}\:{x}={t}^{\mathrm{2}} +\mathrm{2}\:\mathrm{in}\:\mathrm{given}\:\mathrm{equation} \\ $$$$\Rightarrow\:{x}=\frac{\mathrm{66}}{\mathrm{17}} \\ $$

Commented by TawaTawa last updated on 14/Feb/20

$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$

Commented by MJS last updated on 14/Feb/20

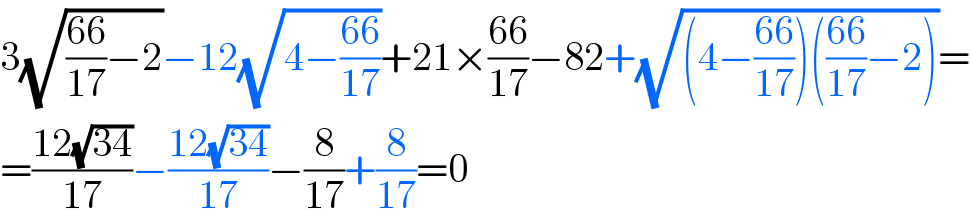
3(√(((66)/(17))−2))−12(√(4−((66)/(17))))+21×((66)/(17))−82+(√((4−((66)/(17)))(((66)/(17))−2)))= =((12(√(34)))/(17))−((12(√(34)))/(17))−(8/(17))+(8/(17))=0

$$\mathrm{3}\sqrt{\frac{\mathrm{66}}{\mathrm{17}}−\mathrm{2}}−\mathrm{12}\sqrt{\mathrm{4}−\frac{\mathrm{66}}{\mathrm{17}}}+\mathrm{21}×\frac{\mathrm{66}}{\mathrm{17}}−\mathrm{82}+\sqrt{\left(\mathrm{4}−\frac{\mathrm{66}}{\mathrm{17}}\right)\left(\frac{\mathrm{66}}{\mathrm{17}}−\mathrm{2}\right)}= \\ $$$$=\frac{\mathrm{12}\sqrt{\mathrm{34}}}{\mathrm{17}}−\frac{\mathrm{12}\sqrt{\mathrm{34}}}{\mathrm{17}}−\frac{\mathrm{8}}{\mathrm{17}}+\frac{\mathrm{8}}{\mathrm{17}}=\mathrm{0} \\ $$

Commented by TawaTawa last updated on 14/Feb/20

Great. God bless you sir. Seen my mistake.

$$\mathrm{Great}.\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}.\:\mathrm{Seen}\:\mathrm{my}\:\mathrm{mistake}. \\ $$

Commented by TawaTawa last updated on 14/Feb/20

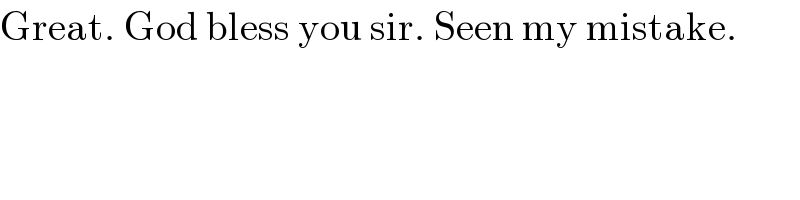
$$\mathrm{Great}.\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}.\:\mathrm{Seen}\:\mathrm{my}\:\mathrm{mistake}. \\ $$

Commented by TawaTawa last updated on 14/Feb/20

Sir, the answer is not satisfy. or i cannot check.

$$\mathrm{Sir},\:\mathrm{the}\:\mathrm{answer}\:\mathrm{is}\:\mathrm{not}\:\mathrm{satisfy}.\:\mathrm{or}\:\mathrm{i}\:\mathrm{cannot}\:\mathrm{check}. \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply