Question Number 81674 by Power last updated on 14/Feb/20
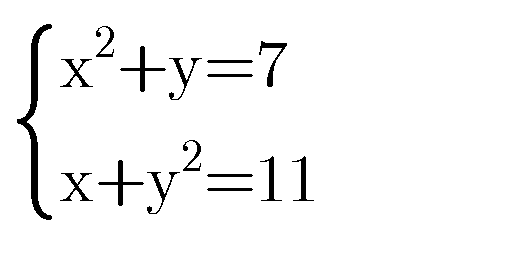
Commented by Tony Lin last updated on 14/Feb/20
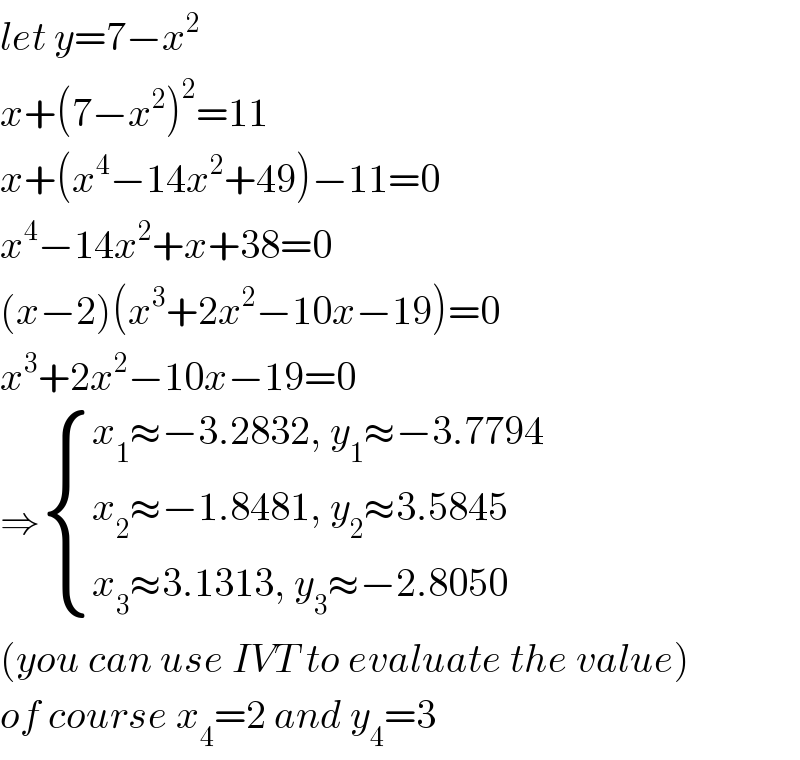
$${let}\:{y}=\mathrm{7}−{x}^{\mathrm{2}} \\ $$$${x}+\left(\mathrm{7}−{x}^{\mathrm{2}} \right)^{\mathrm{2}} =\mathrm{11} \\ $$$${x}+\left({x}^{\mathrm{4}} −\mathrm{14}{x}^{\mathrm{2}} +\mathrm{49}\right)−\mathrm{11}=\mathrm{0} \\ $$$${x}^{\mathrm{4}} −\mathrm{14}{x}^{\mathrm{2}} +{x}+\mathrm{38}=\mathrm{0} \\ $$$$\left({x}−\mathrm{2}\right)\left({x}^{\mathrm{3}} +\mathrm{2}{x}^{\mathrm{2}} −\mathrm{10}{x}−\mathrm{19}\right)=\mathrm{0} \\ $$$${x}^{\mathrm{3}} +\mathrm{2}{x}^{\mathrm{2}} −\mathrm{10}{x}−\mathrm{19}=\mathrm{0} \\ $$$$\Rightarrow\begin{cases}{{x}_{\mathrm{1}} \approx−\mathrm{3}.\mathrm{2832},\:{y}_{\mathrm{1}} \approx−\mathrm{3}.\mathrm{7794}}\\{{x}_{\mathrm{2}} \approx−\mathrm{1}.\mathrm{8481},\:{y}_{\mathrm{2}} \approx\mathrm{3}.\mathrm{5845}}\\{{x}_{\mathrm{3}} \approx\mathrm{3}.\mathrm{1313},\:{y}_{\mathrm{3}} \approx−\mathrm{2}.\mathrm{8050}}\end{cases} \\ $$$$\left({you}\:{can}\:{use}\:{IVT}\:{to}\:{evaluate}\:{the}\:{value}\right) \\ $$$${of}\:{course}\:{x}_{\mathrm{4}} =\mathrm{2}\:{and}\:{y}_{\mathrm{4}} =\mathrm{3}\: \\ $$
Commented by mr W last updated on 14/Feb/20

$${y}=\mathrm{7}−{x}^{\mathrm{2}} \\ $$$${x}+\left(\mathrm{7}−{x}^{\mathrm{2}} \right)^{\mathrm{2}} =\mathrm{11} \\ $$$${x}^{\mathrm{4}} −\mathrm{14}{x}^{\mathrm{2}} +{x}+\mathrm{38}=\mathrm{0} \\ $$$$\left({x}−\mathrm{2}\right)\left({x}^{\mathrm{3}} +\mathrm{2}{x}^{\mathrm{2}} −\mathrm{10}{x}−\mathrm{19}\right)=\mathrm{0} \\ $$$${x}−\mathrm{2}=\mathrm{0}\:\Rightarrow{x}=\mathrm{2}\:\Rightarrow{y}=\mathrm{3} \\ $$$${x}^{\mathrm{3}} +\mathrm{2}{x}^{\mathrm{2}} −\mathrm{10}{x}−\mathrm{19}=\mathrm{0} \\ $$$${let}\:{x}={s}−\frac{\mathrm{2}}{\mathrm{3}} \\ $$$$\Rightarrow{s}^{\mathrm{3}} −\frac{\mathrm{34}}{\mathrm{3}}{s}−\frac{\mathrm{317}}{\mathrm{27}}=\mathrm{0} \\ $$$$\Delta=\left(−\frac{\mathrm{34}}{\mathrm{9}}\right)^{\mathrm{3}} +\left(−\frac{\mathrm{317}}{\mathrm{54}}\right)^{\mathrm{2}} <\mathrm{0} \\ $$$${s}=\frac{\mathrm{2}\sqrt{\mathrm{34}}}{\mathrm{3}}\:\mathrm{sin}\:\left(−\frac{\mathrm{1}}{\mathrm{3}}\mathrm{sin}^{−\mathrm{1}} \frac{\mathrm{317}\sqrt{\mathrm{34}}}{\mathrm{2312}}+\frac{\mathrm{2}{k}\pi}{\mathrm{3}}\right) \\ $$$$\Rightarrow{x}=−\frac{\mathrm{2}}{\mathrm{3}}+\frac{\mathrm{2}\sqrt{\mathrm{34}}}{\mathrm{3}}\:\mathrm{sin}\:\left(−\frac{\mathrm{1}}{\mathrm{3}}\mathrm{sin}^{−\mathrm{1}} \frac{\mathrm{317}\sqrt{\mathrm{34}}}{\mathrm{2312}}+\frac{\mathrm{2}{k}\pi}{\mathrm{3}}\right) \\ $$$$\Rightarrow{x}=−\mathrm{1}.\mathrm{848126}\:\Rightarrow{y}=\mathrm{3}.\mathrm{584427} \\ $$$$\Rightarrow{x}=\mathrm{3}.\mathrm{131313}\:\Rightarrow{y}=−\mathrm{2}.\mathrm{805118} \\ $$$$\Rightarrow{x}=−\mathrm{3}.\mathrm{283186}\:\Rightarrow{y}=−\mathrm{3}.\mathrm{779319} \\ $$
Commented by Power last updated on 14/Feb/20

$$\mathrm{thanks} \\ $$
Answered by Prithwish Sen 1 last updated on 14/Feb/20

$${x}=\mathrm{2} \\ $$$${y}=\mathrm{3} \\ $$
Commented by Power last updated on 14/Feb/20
$$\mathrm{solve}\:\mathrm{sir}\:\:\mathrm{proved} \\ $$
Answered by behi83417@gmail.com last updated on 14/Feb/20
![(x^2 −4)+(y−3)=0 (x−2)+(y^2 −9)=0 ⇒ { (((x−2)(x+2)+(y−3)=0)),(((x−2)+(y−3)(y+3)=0)) :} ⇒ { (((x−2)−(x−2)(x+2)(y+3)=0)),((⇒(x−2)[1−(x+2)(y+3)]=0)) :} ⇒[x−2=0,y^2 =11−2=9⇒y=±3]](https://www.tinkutara.com/question/Q81695.png)
$$\left(\mathrm{x}^{\mathrm{2}} −\mathrm{4}\right)+\left(\mathrm{y}−\mathrm{3}\right)=\mathrm{0} \\ $$$$\left(\mathrm{x}−\mathrm{2}\right)+\left(\mathrm{y}^{\mathrm{2}} −\mathrm{9}\right)=\mathrm{0} \\ $$$$\Rightarrow\begin{cases}{\left(\mathrm{x}−\mathrm{2}\right)\left(\mathrm{x}+\mathrm{2}\right)+\left(\mathrm{y}−\mathrm{3}\right)=\mathrm{0}}\\{\left(\mathrm{x}−\mathrm{2}\right)+\left(\mathrm{y}−\mathrm{3}\right)\left(\mathrm{y}+\mathrm{3}\right)=\mathrm{0}}\end{cases} \\ $$$$\Rightarrow\begin{cases}{\left(\mathrm{x}−\mathrm{2}\right)−\left(\mathrm{x}−\mathrm{2}\right)\left(\mathrm{x}+\mathrm{2}\right)\left(\mathrm{y}+\mathrm{3}\right)=\mathrm{0}}\\{\Rightarrow\left(\mathrm{x}−\mathrm{2}\right)\left[\mathrm{1}−\left(\mathrm{x}+\mathrm{2}\right)\left(\mathrm{y}+\mathrm{3}\right)\right]=\mathrm{0}}\end{cases} \\ $$$$\Rightarrow\left[\mathrm{x}−\mathrm{2}=\mathrm{0},\mathrm{y}^{\mathrm{2}} =\mathrm{11}−\mathrm{2}=\mathrm{9}\Rightarrow\mathrm{y}=\pm\mathrm{3}\right] \\ $$
