Question Number 81698 by peter frank last updated on 14/Feb/20
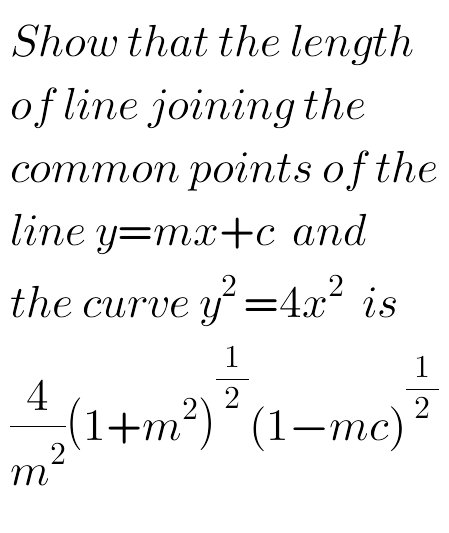
Commented by mr W last updated on 14/Feb/20
$${question}\:{is}\:{wrong}! \\ $$
Answered by mr W last updated on 14/Feb/20

$${y}^{\mathrm{2}} =\mathrm{4}{x}^{\mathrm{2}} \\ $$$$\Rightarrow{y}=\pm\mathrm{2}{x}\:\Rightarrow{two}\:{lines} \\ $$$${y}={mx}+{c}=\mathrm{2}{x} \\ $$$$\Rightarrow{x}_{\mathrm{1}} =\frac{{c}}{\mathrm{2}−{m}},\:{y}_{\mathrm{1}} =\frac{\mathrm{2}{c}}{\mathrm{2}−{m}} \\ $$$${y}={mx}+{c}=−\mathrm{2}{x} \\ $$$$\Rightarrow{x}_{\mathrm{2}} =−\frac{{c}}{\mathrm{2}+{m}},\:{y}_{\mathrm{2}} =\frac{\mathrm{2}{c}}{\mathrm{2}+{m}} \\ $$$$ \\ $$$${distance}=\sqrt{\left({x}_{\mathrm{2}} −{x}_{\mathrm{1}} \right)^{\mathrm{2}} +\left({y}_{\mathrm{2}} −{y}_{\mathrm{1}} \right)^{\mathrm{2}} } \\ $$$$=\sqrt{\left(\frac{{c}}{\mathrm{2}−{m}}+\frac{{c}}{\mathrm{2}+{m}}\right)^{\mathrm{2}} +\left(\frac{\mathrm{2}{c}}{\mathrm{2}−{m}}−\frac{\mathrm{2}{c}}{\mathrm{2}+{m}}\right)^{\mathrm{2}} } \\ $$$$=\frac{\mathrm{4}{c}\sqrt{\mathrm{1}+{m}^{\mathrm{2}} }}{\mathrm{4}−{m}^{\mathrm{2}} } \\ $$
Commented by peter frank last updated on 14/Feb/20
$${thank}\:{you}\:{sir}. \\ $$
