Menu Close

Question-81755

Tinku Tara 0 Comments
Pin




Question Number 81755 by Power last updated on 15/Feb/20
Answered by mr W last updated on 15/Feb/20
Commented by mr W last updated on 15/Feb/20
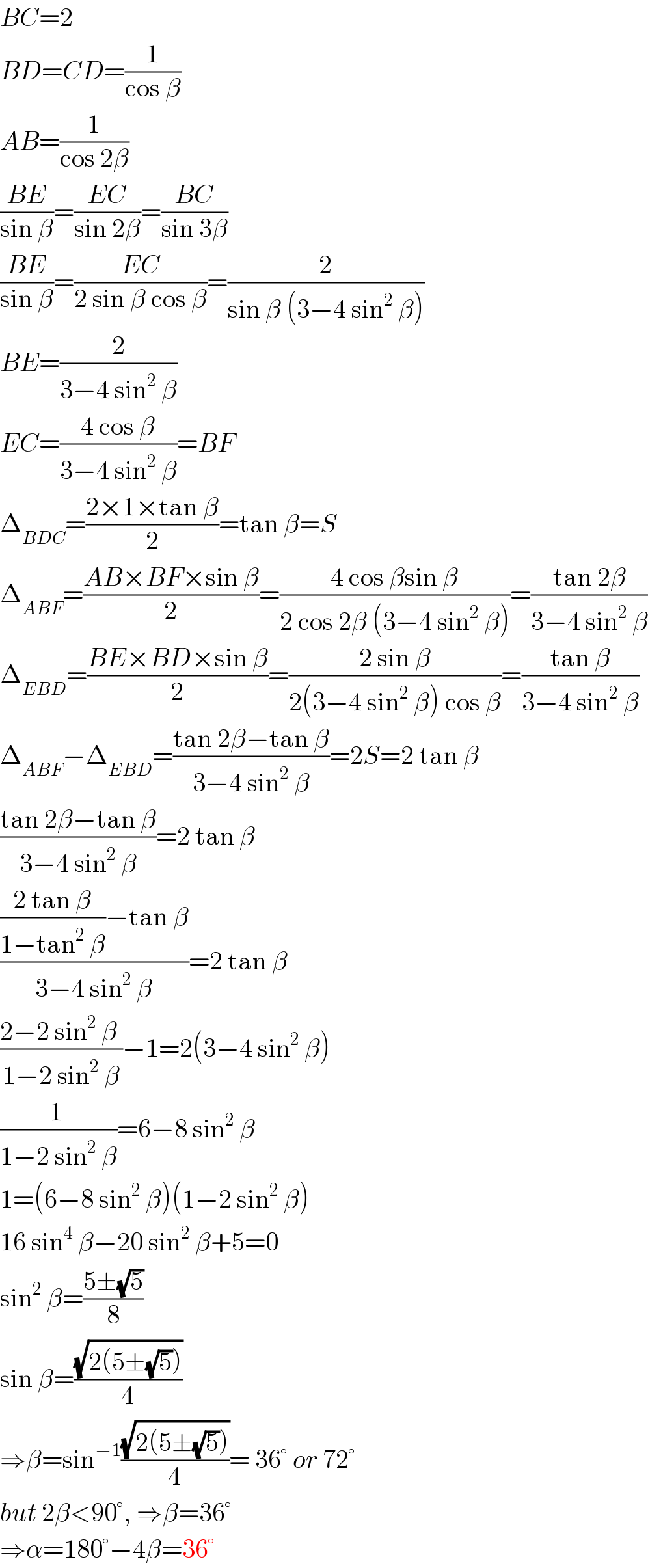
BC=2 BD=CD=(1/(cos β)) AB=(1/(cos 2β)) ((BE)/(sin β))=((EC)/(sin 2β))=((BC)/(sin 3β)) ((BE)/(sin β))=((EC)/(2 sin β cos β))=(2/(sin β (3−4 sin^2 β))) BE=(2/(3−4 sin^2 β)) EC=((4 cos β)/(3−4 sin^2 β))=BF Δ_(BDC) =((2×1×tan β)/2)=tan β=S Δ_(ABF) =((AB×BF×sin β)/2)=((4 cos βsin β)/(2 cos 2β (3−4 sin^2 β)))=((tan 2β)/(3−4 sin^2 β)) Δ_(EBD) =((BE×BD×sin β)/2)=((2 sin β)/(2(3−4 sin^2 β) cos β))=((tan β)/(3−4 sin^2 β)) Δ_(ABF) −Δ_(EBD) =((tan 2β−tan β)/(3−4 sin^2 β))=2S=2 tan β ((tan 2β−tan β)/(3−4 sin^2 β))=2 tan β ((((2 tan β)/(1−tan^2 β))−tan β)/(3−4 sin^2 β))=2 tan β ((2−2 sin^2 β )/(1−2 sin^2 β))−1=2(3−4 sin^2 β) ((1 )/(1−2 sin^2 β))=6−8 sin^2 β 1=(6−8 sin^2 β)(1−2 sin^2 β) 16 sin^4 β−20 sin^2 β+5=0 sin^2 β=((5±(√5))/8) sin β=((√(2(5±(√5))))/4) ⇒β=sin^(−1) ((√(2(5±(√5))))/4)= 36° or 72° but 2β<90°, ⇒β=36° ⇒α=180°−4β=36°
$${BC}=\mathrm{2} \\ $$$${BD}={CD}=\frac{\mathrm{1}}{\mathrm{cos}\:\beta} \\ $$$${AB}=\frac{\mathrm{1}}{\mathrm{cos}\:\mathrm{2}\beta} \\ $$$$\frac{{BE}}{\mathrm{sin}\:\beta}=\frac{{EC}}{\mathrm{sin}\:\mathrm{2}\beta}=\frac{{BC}}{\mathrm{sin}\:\mathrm{3}\beta} \\ $$$$\frac{{BE}}{\mathrm{sin}\:\beta}=\frac{{EC}}{\mathrm{2}\:\mathrm{sin}\:\beta\:\mathrm{cos}\:\beta}=\frac{\mathrm{2}}{\mathrm{sin}\:\beta\:\left(\mathrm{3}−\mathrm{4}\:\mathrm{sin}^{\mathrm{2}} \:\beta\right)} \\ $$$${BE}=\frac{\mathrm{2}}{\mathrm{3}−\mathrm{4}\:\mathrm{sin}^{\mathrm{2}} \:\beta} \\ $$$${EC}=\frac{\mathrm{4}\:\mathrm{cos}\:\beta}{\mathrm{3}−\mathrm{4}\:\mathrm{sin}^{\mathrm{2}} \:\beta}={BF} \\ $$$$\Delta_{{BDC}} =\frac{\mathrm{2}×\mathrm{1}×\mathrm{tan}\:\beta}{\mathrm{2}}=\mathrm{tan}\:\beta={S} \\ $$$$\Delta_{{ABF}} =\frac{{AB}×{BF}×\mathrm{sin}\:\beta}{\mathrm{2}}=\frac{\mathrm{4}\:\mathrm{cos}\:\beta\mathrm{sin}\:\beta}{\mathrm{2}\:\mathrm{cos}\:\mathrm{2}\beta\:\left(\mathrm{3}−\mathrm{4}\:\mathrm{sin}^{\mathrm{2}} \:\beta\right)}=\frac{\mathrm{tan}\:\mathrm{2}\beta}{\mathrm{3}−\mathrm{4}\:\mathrm{sin}^{\mathrm{2}} \:\beta} \\ $$$$\Delta_{{EBD}} =\frac{{BE}×{BD}×\mathrm{sin}\:\beta}{\mathrm{2}}=\frac{\mathrm{2}\:\mathrm{sin}\:\beta}{\mathrm{2}\left(\mathrm{3}−\mathrm{4}\:\mathrm{sin}^{\mathrm{2}} \:\beta\right)\:\mathrm{cos}\:\beta}=\frac{\mathrm{tan}\:\beta}{\mathrm{3}−\mathrm{4}\:\mathrm{sin}^{\mathrm{2}} \:\beta} \\ $$$$\Delta_{{ABF}} −\Delta_{{EBD}} =\frac{\mathrm{tan}\:\mathrm{2}\beta−\mathrm{tan}\:\beta}{\mathrm{3}−\mathrm{4}\:\mathrm{sin}^{\mathrm{2}} \:\beta}=\mathrm{2}{S}=\mathrm{2}\:\mathrm{tan}\:\beta \\ $$$$\frac{\mathrm{tan}\:\mathrm{2}\beta−\mathrm{tan}\:\beta}{\mathrm{3}−\mathrm{4}\:\mathrm{sin}^{\mathrm{2}} \:\beta}=\mathrm{2}\:\mathrm{tan}\:\beta \\ $$$$\frac{\frac{\mathrm{2}\:\mathrm{tan}\:\beta}{\mathrm{1}−\mathrm{tan}^{\mathrm{2}} \:\beta}−\mathrm{tan}\:\beta}{\mathrm{3}−\mathrm{4}\:\mathrm{sin}^{\mathrm{2}} \:\beta}=\mathrm{2}\:\mathrm{tan}\:\beta \\ $$$$\frac{\mathrm{2}−\mathrm{2}\:\mathrm{sin}^{\mathrm{2}} \:\beta\:}{\mathrm{1}−\mathrm{2}\:\mathrm{sin}^{\mathrm{2}} \:\beta}−\mathrm{1}=\mathrm{2}\left(\mathrm{3}−\mathrm{4}\:\mathrm{sin}^{\mathrm{2}} \:\beta\right) \\ $$$$\frac{\mathrm{1}\:}{\mathrm{1}−\mathrm{2}\:\mathrm{sin}^{\mathrm{2}} \:\beta}=\mathrm{6}−\mathrm{8}\:\mathrm{sin}^{\mathrm{2}} \:\beta \\ $$$$\mathrm{1}=\left(\mathrm{6}−\mathrm{8}\:\mathrm{sin}^{\mathrm{2}} \:\beta\right)\left(\mathrm{1}−\mathrm{2}\:\mathrm{sin}^{\mathrm{2}} \:\beta\right) \\ $$$$\mathrm{16}\:\mathrm{sin}^{\mathrm{4}} \:\beta−\mathrm{20}\:\mathrm{sin}^{\mathrm{2}} \:\beta+\mathrm{5}=\mathrm{0} \\ $$$$\mathrm{sin}^{\mathrm{2}} \:\beta=\frac{\mathrm{5}\pm\sqrt{\mathrm{5}}}{\mathrm{8}} \\ $$$$\mathrm{sin}\:\beta=\frac{\sqrt{\mathrm{2}\left(\mathrm{5}\pm\sqrt{\mathrm{5}}\right)}}{\mathrm{4}} \\ $$$$\Rightarrow\beta=\mathrm{sin}^{−\mathrm{1}} \frac{\sqrt{\mathrm{2}\left(\mathrm{5}\pm\sqrt{\mathrm{5}}\right)}}{\mathrm{4}}=\:\mathrm{36}°\:{or}\:\mathrm{72}° \\ $$$${but}\:\mathrm{2}\beta<\mathrm{90}°,\:\Rightarrow\beta=\mathrm{36}° \\ $$$$\Rightarrow\alpha=\mathrm{180}°−\mathrm{4}\beta=\mathrm{36}° \\ $$
Commented by Power last updated on 15/Feb/20
great sir
$$\mathrm{great}\:\mathrm{sir} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *