Question Number 81771 by Power last updated on 15/Feb/20
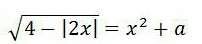
Commented by Power last updated on 15/Feb/20

$$\mathrm{solution} \\ $$
Commented by Power last updated on 15/Feb/20
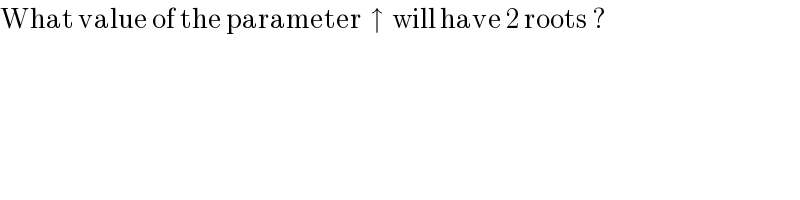
$$\mathrm{What}\:\mathrm{value}\:\mathrm{of}\:\mathrm{the}\:\mathrm{parameter}\:\:\uparrow\:\:\mathrm{will}\:\mathrm{have}\:\mathrm{2}\:\mathrm{roots}\:? \\ $$
Commented by mr W last updated on 15/Feb/20
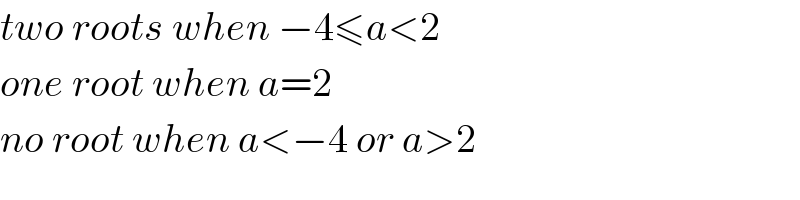
$${two}\:{roots}\:{when}\:−\mathrm{4}\leqslant{a}<\mathrm{2} \\ $$$${one}\:{root}\:{when}\:{a}=\mathrm{2} \\ $$$${no}\:{root}\:{when}\:{a}<−\mathrm{4}\:{or}\:{a}>\mathrm{2} \\ $$
Answered by mr W last updated on 15/Feb/20

$${let}\:{f}\left({x}\right)=\sqrt{\mathrm{4}−\mid\mathrm{2}{x}\mid} \\ $$$${let}\:{g}\left({x}\right)={x}^{\mathrm{2}} +{a} \\ $$$${both}\:{functions}\:{are}\:{even},\:{i}.{e}.\: \\ $$$${f}\left(−{x}\right)={f}\left({x}\right),\:{g}\left(−{x}\right)={g}\left({x}\right) \\ $$$${we}\:{only}\:{need}\:{to}\:{look}\:{at}\:{x}\geqslant\mathrm{0}. \\ $$$${f}\left({x}\right)=\sqrt{\mathrm{4}−\mathrm{2}{x}}\:: \\ $$$$\mathrm{0}\leqslant{x}\leqslant\mathrm{2} \\ $$$${f}\left(\mathrm{0}\right)=\mathrm{2}={maximum} \\ $$$${f}\left(\mathrm{2}\right)=\mathrm{0}={minimum} \\ $$$${g}\left({x}\right)={x}^{\mathrm{2}} +{a}\:: \\ $$$${this}\:{is}\:{a}\:{parabola}\:{opening}\:{upwards}, \\ $$$${its}\:{lowest}\:{point}\:{is}\:\left(\mathrm{0},{a}\right). \\ $$$$ \\ $$$${such}\:{that}\:{the}\:{eqn}.\:{has}\:{two}\:{roots},\:{the} \\ $$$${curve}\:{g}\left({x}\right)\:{must}\:{intersect}\:{the}\:{curve}\:{g}\left({x}\right) \\ $$$${at}\:{two}\:{points}. \\ $$$${we}\:{have}\:{following}\:{cases}: \\ $$$$ \\ $$$${case}\:\mathrm{1}:\:{a}>\mathrm{2},\:{g}\left({x}\right)\:{is}\:{too}\:{high}\:{and}\:{can}'{t} \\ $$$${intersect}\:{the}\:{curve}\:{f}\left({x}\right)\:\Rightarrow{no}\:{root}. \\ $$$$ \\ $$$${case}\:\mathrm{2}:\:{a}=\mathrm{2},\:{the}\:{lowest}\:{point}\:{of}\:{g}\left({x}\right)\: \\ $$$${coincides}\:{with}\:{the}\:{topmost}\:{point}\:{of} \\ $$$${f}\left({x}\right),\:{one}\:{intersection}\:{point}\:\Rightarrow{one} \\ $$$${root}. \\ $$$$ \\ $$$${case}\:\mathrm{3}:\:−\mathrm{4}\leqslant{a}<\mathrm{2},\:{g}\left({x}\right)\:{intersects}\:{with} \\ $$$${f}\left({x}\right)\:{at}\:{two}\:{points}\:\Rightarrow{two}\:{roots}. \\ $$$$ \\ $$$${case}\:\mathrm{4}:\:{a}=−\mathrm{4},\:{y}={x}^{\mathrm{2}} −\mathrm{4},\:{y}=\mathrm{0}\:\Rightarrow{x}=\pm\mathrm{2}. \\ $$$${f}\left({x}\right)\:{intersects}\:{with}\:{g}\left({x}\right)\:{at}\:\left(−\mathrm{2},\mathrm{0}\right)\:{and} \\ $$$$\left(\mathrm{2},\mathrm{0}\right)\Rightarrow{two}\:{roots}. \\ $$$$ \\ $$$${case}\:\mathrm{5}:\:{a}<−\mathrm{4},\:{g}\left({x}\right)\:{is}\:{too}\:{low}\:{and}\:{can}'{t} \\ $$$${intersect}\:{with}\:{f}\left({x}\right)\Rightarrow{no}\:{root}. \\ $$
Commented by mr W last updated on 15/Feb/20

Commented by Power last updated on 15/Feb/20

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir} \\ $$
Commented by mr W last updated on 15/Feb/20
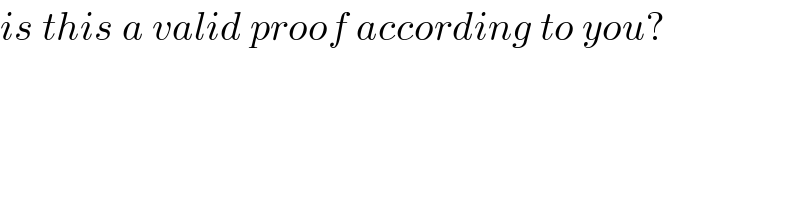
$${is}\:{this}\:{a}\:{valid}\:{proof}\:{according}\:{to}\:{you}? \\ $$
Commented by Power last updated on 15/Feb/20

$$\mathrm{yes}\:\mathrm{sir} \\ $$
