Question-81786

Question Number 81786 by M±th+et£s last updated on 15/Feb/20

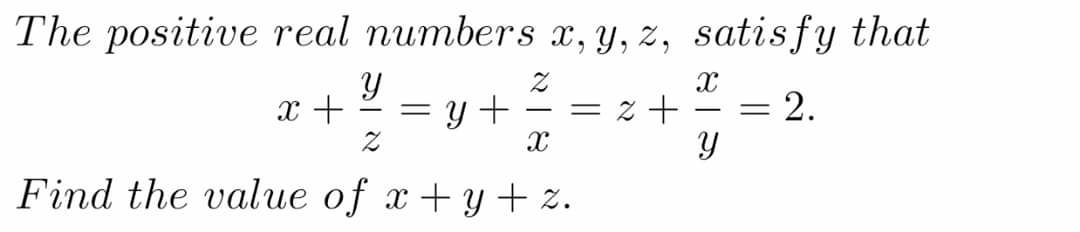
Commented by M±th+et£s last updated on 16/Feb/20

no its right no problem with tbe ans but i need to now how you get (x,y,z)=(1,1,1)

$${no}\:{its}\:{right}\:{no}\:{problem}\:{with}\:{tbe}\:{ans} \\ $$$${but}\:{i}\:{need}\:{to}\:{now}\:{how}\:{you}\:{get}\:\left({x},{y},{z}\right)=\left(\mathrm{1},\mathrm{1},\mathrm{1}\right) \\ $$

Commented by john santu last updated on 15/Feb/20

x+(y/z)=2 y+(z/x)=2 z+(x/y)=2 ⇒(x+y+z)+(y/z)+(z/x)+(x/y)=6 (x+y+z)+((z^2 +xy)/(xz))+(x/y)=6 (x+y+z)+((yz^2 +xy^2 +x^2 z)/(xyz))=6 (∗) (x+(y/z))(y+(z/x))(z+(x/y))=8 (xy+z+(y^2 /z)+(y/x))(z+(x/y))=8 (xyz+x^2 +z^2 +((xz)/y)+y^2 +((xy)/z)+((yz)/x)+1)=8 x^2 +y^2 +z^2 +xyz+((xz)/y)+((xy)/z)+((yz)/x)=7 x^2 +y^2 +z^2 +xyz+((xz^2 +xy^2 )/(yz))+((yz)/x)=7 x^2 +y^2 +z^2 +xyz+((x^2 z^2 +x^2 y^2 +y^2 z^2 )/(xyz))=7

$${x}+\frac{{y}}{{z}}=\mathrm{2} \\ $$$${y}+\frac{{z}}{{x}}=\mathrm{2} \\ $$$${z}+\frac{{x}}{{y}}=\mathrm{2} \\ $$$$\Rightarrow\left({x}+{y}+{z}\right)+\frac{{y}}{{z}}+\frac{{z}}{{x}}+\frac{{x}}{{y}}=\mathrm{6} \\ $$$$\left({x}+{y}+{z}\right)+\frac{{z}^{\mathrm{2}} +{xy}}{{xz}}+\frac{{x}}{{y}}=\mathrm{6} \\ $$$$\left({x}+{y}+{z}\right)+\frac{{yz}^{\mathrm{2}} +{xy}^{\mathrm{2}} +{x}^{\mathrm{2}} {z}}{{xyz}}=\mathrm{6}\:\left(\ast\right) \\ $$$$\left({x}+\frac{{y}}{{z}}\right)\left({y}+\frac{{z}}{{x}}\right)\left({z}+\frac{{x}}{{y}}\right)=\mathrm{8} \\ $$$$\left({xy}+{z}+\frac{{y}^{\mathrm{2}} }{{z}}+\frac{{y}}{{x}}\right)\left({z}+\frac{{x}}{{y}}\right)=\mathrm{8} \\ $$$$\left({xyz}+{x}^{\mathrm{2}} +{z}^{\mathrm{2}} +\frac{{xz}}{{y}}+{y}^{\mathrm{2}} +\frac{{xy}}{{z}}+\frac{{yz}}{{x}}+\mathrm{1}\right)=\mathrm{8} \\ $$$${x}^{\mathrm{2}} +{y}^{\mathrm{2}} +{z}^{\mathrm{2}} +{xyz}+\frac{{xz}}{{y}}+\frac{{xy}}{{z}}+\frac{{yz}}{{x}}=\mathrm{7} \\ $$$${x}^{\mathrm{2}} +{y}^{\mathrm{2}} +{z}^{\mathrm{2}} +{xyz}+\frac{{xz}^{\mathrm{2}} +{xy}^{\mathrm{2}} }{{yz}}+\frac{{yz}}{{x}}=\mathrm{7} \\ $$$${x}^{\mathrm{2}} +{y}^{\mathrm{2}} +{z}^{\mathrm{2}} +{xyz}+\frac{{x}^{\mathrm{2}} {z}^{\mathrm{2}} +{x}^{\mathrm{2}} {y}^{\mathrm{2}} +{y}^{\mathrm{2}} {z}^{\mathrm{2}} }{{xyz}}=\mathrm{7} \\ $$$$ \\ $$

Commented by john santu last updated on 15/Feb/20

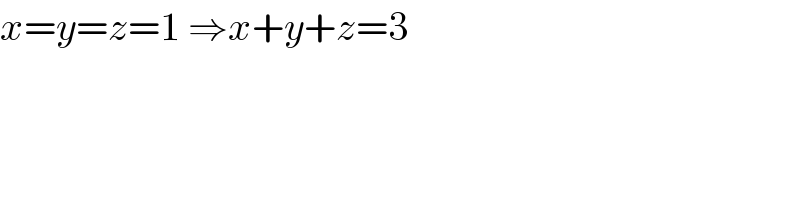
$${x}={y}={z}=\mathrm{1}\:\Rightarrow{x}+{y}+{z}=\mathrm{3} \\ $$

Commented by M±th+et£s last updated on 15/Feb/20

thank you sir for ghis solution . I want mention that the numbers are real posative how did you conclude that the only of there numbers is(1,1,1), I guess that needs some pfoofs.we are interested in finding the sum instead of there numbers values .

$${thank}\:{you}\:{sir}\:{for}\:{ghis}\:{solution}\:.\:{I}\:{want} \\ $$$${mention}\:{that}\:{the}\:{numbers}\:{are}\:{real}\:{posative} \\ $$$${how}\:{did}\:{you}\:{conclude}\:{that}\:{the}\:{only}\:{of} \\ $$$${there}\:{numbers}\:{is}\left(\mathrm{1},\mathrm{1},\mathrm{1}\right),\:{I}\:{guess}\:{that}\: \\ $$$${needs}\:{some}\:{pfoofs}.{we}\:{are}\:{interested} \\ $$$${in}\:{finding}\:{the}\:{sum}\:{instead}\:{of}\:{there}\: \\ $$$${numbers}\:{values}\:.\: \\ $$

Commented by john santu last updated on 16/Feb/20

$${my}\:{ans}\:{is}\:{wrong}? \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply