Menu Close

Question-81824

Tinku Tara 0 Comments
Pin




Question Number 81824 by M±th+et£s last updated on 15/Feb/20
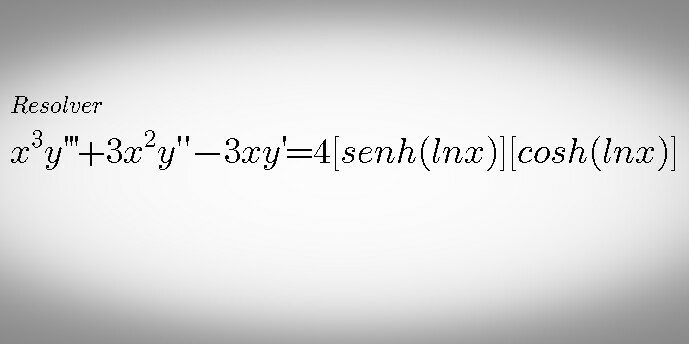
Answered by mind is power last updated on 17/Feb/20
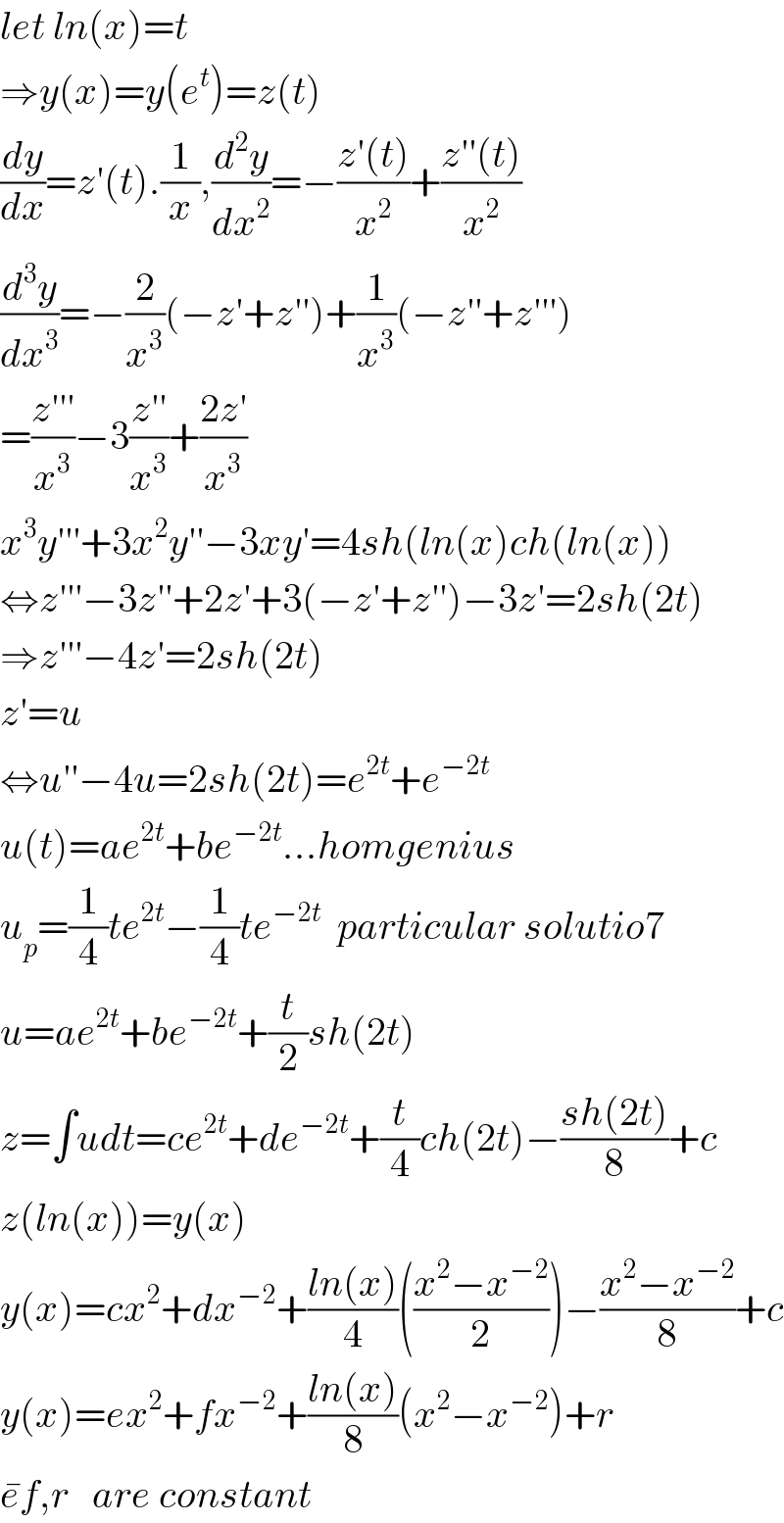
let ln(x)=t ⇒y(x)=y(e^t )=z(t) (dy/dx)=z′(t).(1/x),(d^2 y/dx^2 )=−((z′(t))/x^2 )+((z′′(t))/x^2 ) (d^3 y/dx^3 )=−(2/x^3 )(−z′+z′′)+(1/x^3 )(−z′′+z′′′) =((z′′′)/x^3 )−3((z′′)/x^3 )+((2z′)/x^3 ) x^3 y′′′+3x^2 y′′−3xy′=4sh(ln(x)ch(ln(x)) ⇔z′′′−3z′′+2z′+3(−z′+z′′)−3z′=2sh(2t) ⇒z′′′−4z′=2sh(2t) z′=u ⇔u′′−4u=2sh(2t)=e^(2t) +e^(−2t) u(t)=ae^(2t) +be^(−2t) ...homgenius u_p =(1/4)te^(2t) −(1/4)te^(−2t) particular solutio7 u=ae^(2t) +be^(−2t) +(t/2)sh(2t) z=∫udt=ce^(2t) +de^(−2t) +(t/4)ch(2t)−((sh(2t))/8)+c z(ln(x))=y(x) y(x)=cx^2 +dx^(−2) +((ln(x))/4)(((x^2 −x^(−2) )/2))−((x^2 −x^(−2) )/8)+c y(x)=ex^2 +fx^(−2) +((ln(x))/8)(x^2 −x^(−2) )+r e^� f,r are constant
$${let}\:{ln}\left({x}\right)={t} \\ $$$$\Rightarrow{y}\left({x}\right)={y}\left({e}^{{t}} \right)={z}\left({t}\right) \\ $$$$\frac{{dy}}{{dx}}={z}'\left({t}\right).\frac{\mathrm{1}}{{x}},\frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} }=−\frac{{z}'\left({t}\right)}{{x}^{\mathrm{2}} }+\frac{{z}''\left({t}\right)}{{x}^{\mathrm{2}} } \\ $$$$\frac{{d}^{\mathrm{3}} {y}}{{dx}^{\mathrm{3}} }=−\frac{\mathrm{2}}{{x}^{\mathrm{3}} }\left(−{z}'+{z}''\right)+\frac{\mathrm{1}}{{x}^{\mathrm{3}} }\left(−{z}''+{z}'''\right) \\ $$$$=\frac{{z}'''}{{x}^{\mathrm{3}} }−\mathrm{3}\frac{{z}''}{{x}^{\mathrm{3}} }+\frac{\mathrm{2}{z}'}{{x}^{\mathrm{3}} } \\ $$$${x}^{\mathrm{3}} {y}'''+\mathrm{3}{x}^{\mathrm{2}} {y}''−\mathrm{3}{xy}'=\mathrm{4}{sh}\left({ln}\left({x}\right){ch}\left({ln}\left({x}\right)\right)\right. \\ $$$$\Leftrightarrow{z}'''−\mathrm{3}{z}''+\mathrm{2}{z}'+\mathrm{3}\left(−{z}'+{z}''\right)−\mathrm{3}{z}'=\mathrm{2}{sh}\left(\mathrm{2}{t}\right) \\ $$$$\Rightarrow{z}'''−\mathrm{4}{z}'=\mathrm{2}{sh}\left(\mathrm{2}{t}\right) \\ $$$${z}'={u} \\ $$$$\Leftrightarrow{u}''−\mathrm{4}{u}=\mathrm{2}{sh}\left(\mathrm{2}{t}\right)={e}^{\mathrm{2}{t}} +{e}^{−\mathrm{2}{t}} \\ $$$${u}\left({t}\right)={ae}^{\mathrm{2}{t}} +{be}^{−\mathrm{2}{t}} …{homgenius} \\ $$$${u}_{{p}} =\frac{\mathrm{1}}{\mathrm{4}}{te}^{\mathrm{2}{t}} −\frac{\mathrm{1}}{\mathrm{4}}{te}^{−\mathrm{2}{t}} \:\:{particular}\:{solutio}\mathrm{7} \\ $$$${u}={ae}^{\mathrm{2}{t}} +{be}^{−\mathrm{2}{t}} +\frac{{t}}{\mathrm{2}}{sh}\left(\mathrm{2}{t}\right) \\ $$$${z}=\int{udt}={ce}^{\mathrm{2}{t}} +{de}^{−\mathrm{2}{t}} +\frac{{t}}{\mathrm{4}}{ch}\left(\mathrm{2}{t}\right)−\frac{{sh}\left(\mathrm{2}{t}\right)}{\mathrm{8}}+{c} \\ $$$${z}\left({ln}\left({x}\right)\right)={y}\left({x}\right) \\ $$$${y}\left({x}\right)={cx}^{\mathrm{2}} +{dx}^{−\mathrm{2}} +\frac{{ln}\left({x}\right)}{\mathrm{4}}\left(\frac{{x}^{\mathrm{2}} −{x}^{−\mathrm{2}} }{\mathrm{2}}\right)−\frac{{x}^{\mathrm{2}} −{x}^{−\mathrm{2}} }{\mathrm{8}}+{c} \\ $$$${y}\left({x}\right)={ex}^{\mathrm{2}} +{fx}^{−\mathrm{2}} +\frac{{ln}\left({x}\right)}{\mathrm{8}}\left({x}^{\mathrm{2}} −{x}^{−\mathrm{2}} \right)+{r} \\ $$$$\bar {{e}f},{r}\:\:\:{are}\:{constant} \\ $$
Commented by M±th+et£s last updated on 17/Feb/20
god bless you
$${god}\:{bless}\:{you} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *