Question Number 81843 by TawaTawa last updated on 15/Feb/20

Commented by mr W last updated on 16/Feb/20

Commented by mr W last updated on 16/Feb/20
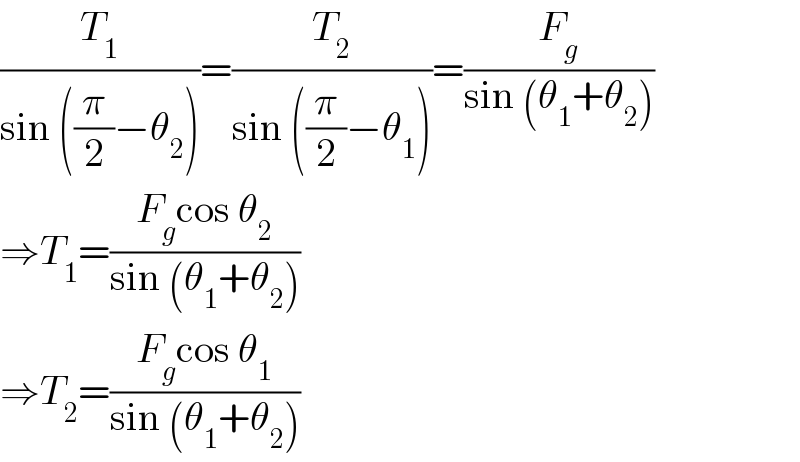
$$\frac{{T}_{\mathrm{1}} }{\mathrm{sin}\:\left(\frac{\pi}{\mathrm{2}}−\theta_{\mathrm{2}} \right)}=\frac{{T}_{\mathrm{2}} }{\mathrm{sin}\:\left(\frac{\pi}{\mathrm{2}}−\theta_{\mathrm{1}} \right)}=\frac{{F}_{{g}} }{\mathrm{sin}\:\left(\theta_{\mathrm{1}} +\theta_{\mathrm{2}} \right)} \\ $$$$\Rightarrow{T}_{\mathrm{1}} =\frac{{F}_{{g}} \mathrm{cos}\:\theta_{\mathrm{2}} }{\mathrm{sin}\:\left(\theta_{\mathrm{1}} +\theta_{\mathrm{2}} \right)} \\ $$$$\Rightarrow{T}_{\mathrm{2}} =\frac{{F}_{{g}} \mathrm{cos}\:\theta_{\mathrm{1}} }{\mathrm{sin}\:\left(\theta_{\mathrm{1}} +\theta_{\mathrm{2}} \right)} \\ $$
Commented by TawaTawa last updated on 15/Feb/20

$$\mathrm{Please}\:\mathrm{help}\:\mathrm{me}. \\ $$
Commented by TawaTawa last updated on 15/Feb/20

$$\mathrm{Please}\:\mathrm{help}\:\mathrm{me}. \\ $$
Commented by TawaTawa last updated on 16/Feb/20
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}.\:\mathrm{I}\:\mathrm{appreciate}\:\mathrm{your}\:\mathrm{time} \\ $$
Answered by ajfour last updated on 15/Feb/20

Commented by ajfour last updated on 15/Feb/20
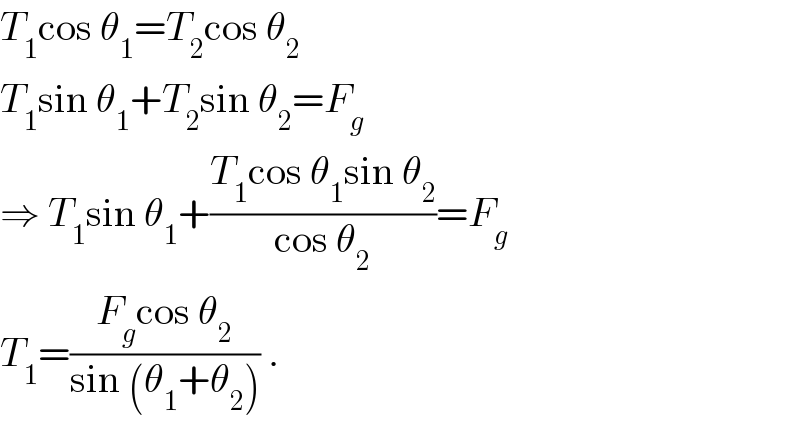
$${T}_{\mathrm{1}} \mathrm{cos}\:\theta_{\mathrm{1}} ={T}_{\mathrm{2}} \mathrm{cos}\:\theta_{\mathrm{2}} \\ $$$${T}_{\mathrm{1}} \mathrm{sin}\:\theta_{\mathrm{1}} +{T}_{\mathrm{2}} \mathrm{sin}\:\theta_{\mathrm{2}} ={F}_{{g}} \\ $$$$\Rightarrow\:{T}_{\mathrm{1}} \mathrm{sin}\:\theta_{\mathrm{1}} +\frac{{T}_{\mathrm{1}} \mathrm{cos}\:\theta_{\mathrm{1}} \mathrm{sin}\:\theta_{\mathrm{2}} }{\mathrm{cos}\:\theta_{\mathrm{2}} }={F}_{{g}} \\ $$$${T}_{\mathrm{1}} =\frac{{F}_{{g}} \mathrm{cos}\:\theta_{\mathrm{2}} }{\mathrm{sin}\:\left(\theta_{\mathrm{1}} +\theta_{\mathrm{2}} \right)}\:. \\ $$
Commented by TawaTawa last updated on 16/Feb/20
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}.\:\mathrm{I}\:\mathrm{appreciate}\:\mathrm{your}\:\mathrm{time} \\ $$
Answered by mind is power last updated on 15/Feb/20
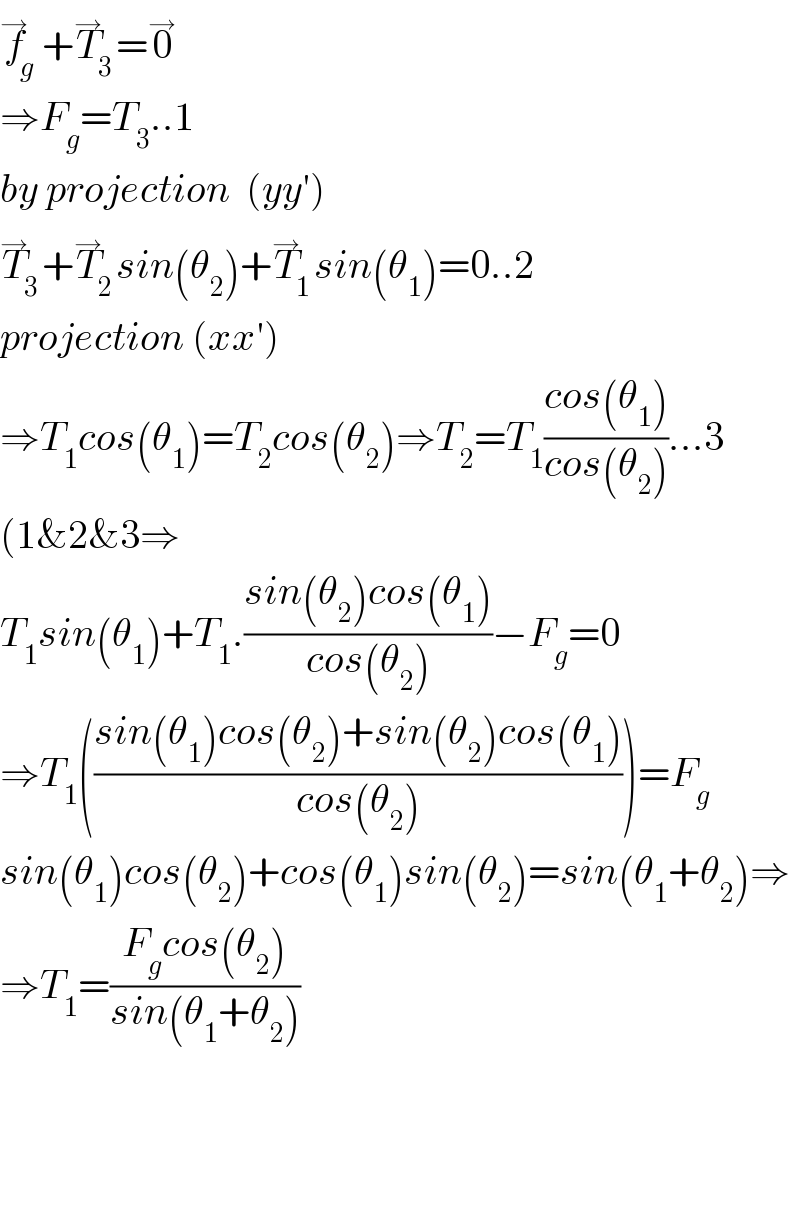
$$\overset{\rightarrow} {{f}}_{{g}} +\overset{\rightarrow} {{T}}_{\mathrm{3}} =\overset{\rightarrow} {\mathrm{0}} \\ $$$$\Rightarrow{F}_{{g}} ={T}_{\mathrm{3}} ..\mathrm{1} \\ $$$${by}\:{projection}\:\:\left({yy}'\right) \\ $$$$\overset{\rightarrow} {{T}}_{\mathrm{3}} +\overset{\rightarrow} {{T}}_{\mathrm{2}} {sin}\left(\theta_{\mathrm{2}} \right)+\overset{\rightarrow} {{T}}_{\mathrm{1}} {sin}\left(\theta_{\mathrm{1}} \right)=\mathrm{0}..\mathrm{2} \\ $$$${projection}\:\left({xx}'\right) \\ $$$$\Rightarrow{T}_{\mathrm{1}} {cos}\left(\theta_{\mathrm{1}} \right)={T}_{\mathrm{2}} {cos}\left(\theta_{\mathrm{2}} \right)\Rightarrow{T}_{\mathrm{2}} ={T}_{\mathrm{1}} \frac{{cos}\left(\theta_{\mathrm{1}} \right)}{{cos}\left(\theta_{\mathrm{2}} \right)}…\mathrm{3} \\ $$$$\left(\mathrm{1\&2\&3}\Rightarrow\right. \\ $$$${T}_{\mathrm{1}} {sin}\left(\theta_{\mathrm{1}} \right)+{T}_{\mathrm{1}} .\frac{{sin}\left(\theta_{\mathrm{2}} \right){cos}\left(\theta_{\mathrm{1}} \right)}{{cos}\left(\theta_{\mathrm{2}} \right)}−{F}_{{g}} =\mathrm{0} \\ $$$$\Rightarrow{T}_{\mathrm{1}} \left(\frac{{sin}\left(\theta_{\mathrm{1}} \right){cos}\left(\theta_{\mathrm{2}} \right)+{sin}\left(\theta_{\mathrm{2}} \right){cos}\left(\theta_{\mathrm{1}} \right)}{{cos}\left(\theta_{\mathrm{2}} \right)}\right)={F}_{{g}} \\ $$$${sin}\left(\theta_{\mathrm{1}} \right){cos}\left(\theta_{\mathrm{2}} \right)+{cos}\left(\theta_{\mathrm{1}} \right){sin}\left(\theta_{\mathrm{2}} \right)={sin}\left(\theta_{\mathrm{1}} +\theta_{\mathrm{2}} \right)\Rightarrow \\ $$$$\Rightarrow{T}_{\mathrm{1}} =\frac{{F}_{{g}} {cos}\left(\theta_{\mathrm{2}} \right)}{{sin}\left(\theta_{\mathrm{1}} +\theta_{\mathrm{2}} \right)} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
Commented by TawaTawa last updated on 16/Feb/20
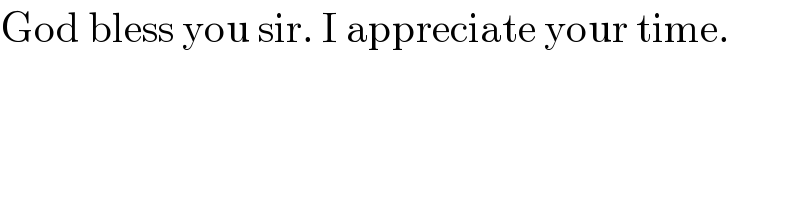
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}.\:\mathrm{I}\:\mathrm{appreciate}\:\mathrm{your}\:\mathrm{time}. \\ $$
Commented by mind is power last updated on 16/Feb/20
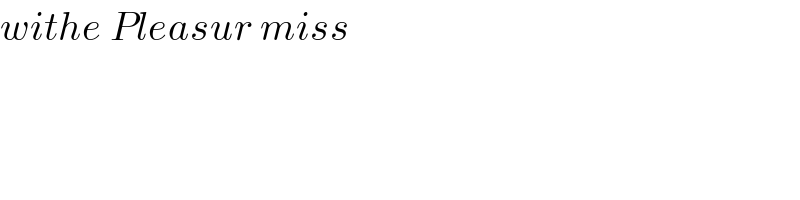
$${withe}\:{Pleasur}\:{miss} \\ $$
