Question-81892

Question Number 81892 by Power last updated on 16/Feb/20

Answered by MJS last updated on 16/Feb/20

we can find a formula for any value of the next number ⇒ the answer is not unique

$$\mathrm{we}\:\mathrm{can}\:\mathrm{find}\:\mathrm{a}\:\mathrm{formula}\:\mathrm{for}\:\mathrm{any}\:\mathrm{value}\:\mathrm{of}\:\mathrm{the} \\ $$$$\mathrm{next}\:\mathrm{number}\:\Rightarrow\:\mathrm{the}\:\mathrm{answer}\:\mathrm{is}\:\mathrm{not}\:\mathrm{unique} \\ $$

Commented by mr W last updated on 16/Feb/20

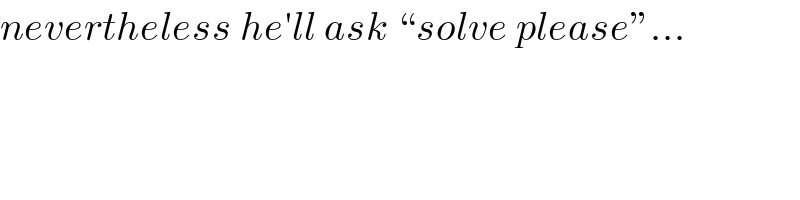
$${nevertheless}\:{he}'{ll}\:{ask}\:“{solve}\:{please}''… \\ $$

Answered by MJS last updated on 16/Feb/20

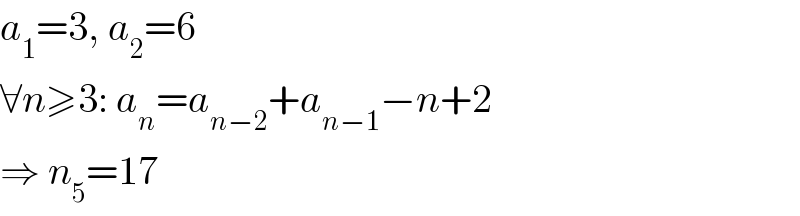
a_1 =3, a_2 =6 ∀n≥3: a_n =a_(n−2) +a_(n−1) −n+2 ⇒ n_5 =17

$${a}_{\mathrm{1}} =\mathrm{3},\:{a}_{\mathrm{2}} =\mathrm{6} \\ $$$$\forall{n}\geqslant\mathrm{3}:\:{a}_{{n}} ={a}_{{n}−\mathrm{2}} +{a}_{{n}−\mathrm{1}} −{n}+\mathrm{2} \\ $$$$\Rightarrow\:{n}_{\mathrm{5}} =\mathrm{17} \\ $$

Answered by MJS last updated on 16/Feb/20

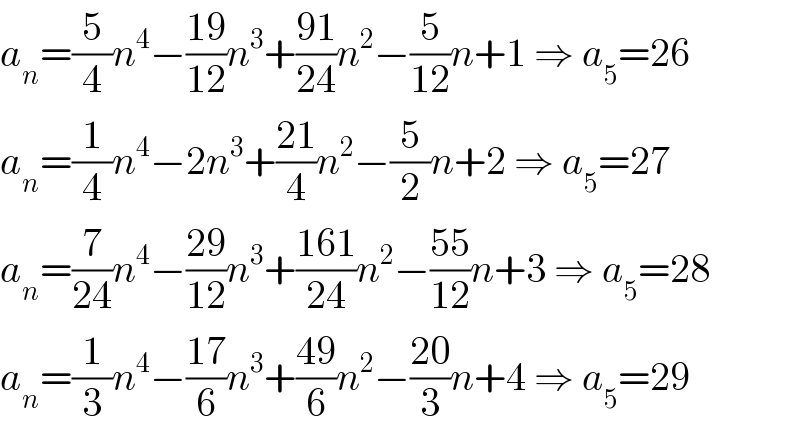
a_n =(5/4)n^4 −((19)/(12))n^3 +((91)/(24))n^2 −(5/(12))n+1 ⇒ a_5 =26 a_n =(1/4)n^4 −2n^3 +((21)/4)n^2 −(5/2)n+2 ⇒ a_5 =27 a_n =(7/(24))n^4 −((29)/(12))n^3 +((161)/(24))n^2 −((55)/(12))n+3 ⇒ a_5 =28 a_n =(1/3)n^4 −((17)/6)n^3 +((49)/6)n^2 −((20)/3)n+4 ⇒ a_5 =29

$${a}_{{n}} =\frac{\mathrm{5}}{\mathrm{4}}{n}^{\mathrm{4}} −\frac{\mathrm{19}}{\mathrm{12}}{n}^{\mathrm{3}} +\frac{\mathrm{91}}{\mathrm{24}}{n}^{\mathrm{2}} −\frac{\mathrm{5}}{\mathrm{12}}{n}+\mathrm{1}\:\Rightarrow\:{a}_{\mathrm{5}} =\mathrm{26} \\ $$$${a}_{{n}} =\frac{\mathrm{1}}{\mathrm{4}}{n}^{\mathrm{4}} −\mathrm{2}{n}^{\mathrm{3}} +\frac{\mathrm{21}}{\mathrm{4}}{n}^{\mathrm{2}} −\frac{\mathrm{5}}{\mathrm{2}}{n}+\mathrm{2}\:\Rightarrow\:{a}_{\mathrm{5}} =\mathrm{27} \\ $$$${a}_{{n}} =\frac{\mathrm{7}}{\mathrm{24}}{n}^{\mathrm{4}} −\frac{\mathrm{29}}{\mathrm{12}}{n}^{\mathrm{3}} +\frac{\mathrm{161}}{\mathrm{24}}{n}^{\mathrm{2}} −\frac{\mathrm{55}}{\mathrm{12}}{n}+\mathrm{3}\:\Rightarrow\:{a}_{\mathrm{5}} =\mathrm{28} \\ $$$${a}_{{n}} =\frac{\mathrm{1}}{\mathrm{3}}{n}^{\mathrm{4}} −\frac{\mathrm{17}}{\mathrm{6}}{n}^{\mathrm{3}} +\frac{\mathrm{49}}{\mathrm{6}}{n}^{\mathrm{2}} −\frac{\mathrm{20}}{\mathrm{3}}{n}+\mathrm{4}\:\Rightarrow\:{a}_{\mathrm{5}} =\mathrm{29} \\ $$

Answered by MJS last updated on 16/Feb/20

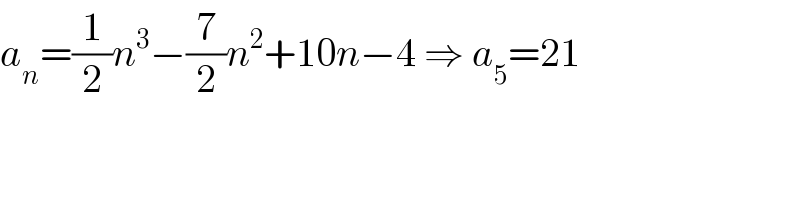
a_n =(1/2)n^3 −(7/2)n^2 +10n−4 ⇒ a_5 =21

$${a}_{{n}} =\frac{\mathrm{1}}{\mathrm{2}}{n}^{\mathrm{3}} −\frac{\mathrm{7}}{\mathrm{2}}{n}^{\mathrm{2}} +\mathrm{10}{n}−\mathrm{4}\:\Rightarrow\:{a}_{\mathrm{5}} =\mathrm{21} \\ $$

Answered by MJS last updated on 16/Feb/20

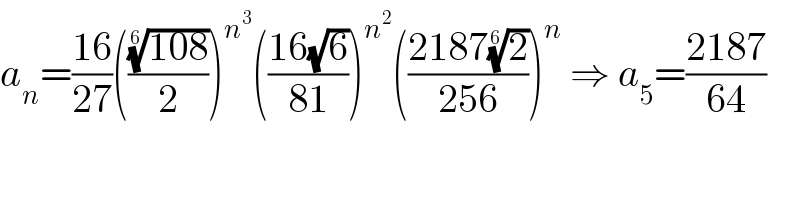
a_n =((16)/(27))((((108))^(1/6) /2))^n^3 (((16(√6))/(81)))^n^2 (((2187(2)^(1/6) )/(256)))^n ⇒ a_5 =((2187)/(64))

$${a}_{{n}} =\frac{\mathrm{16}}{\mathrm{27}}\left(\frac{\sqrt[{\mathrm{6}}]{\mathrm{108}}}{\mathrm{2}}\right)^{{n}^{\mathrm{3}} } \left(\frac{\mathrm{16}\sqrt{\mathrm{6}}}{\mathrm{81}}\right)^{{n}^{\mathrm{2}} } \left(\frac{\mathrm{2187}\sqrt[{\mathrm{6}}]{\mathrm{2}}}{\mathrm{256}}\right)^{{n}} \:\Rightarrow\:{a}_{\mathrm{5}} =\frac{\mathrm{2187}}{\mathrm{64}} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply