Question Number 81911 by jagoll last updated on 16/Feb/20

Commented by jagoll last updated on 16/Feb/20

$${a}_{{n}+\mathrm{1}} \:=\:\frac{\mathrm{3}{a}_{{n}} +\mathrm{1}}{\mathrm{2}}\: \\ $$$${a}_{{n}+\mathrm{1}} \:+{A}\:=\:{A}+\frac{\mathrm{3}{a}_{{n}} +\mathrm{1}}{\mathrm{2}}=\frac{\mathrm{3}{a}_{{n}} +\mathrm{2}{A}+\mathrm{1}}{\mathrm{2}} \\ $$$${a}_{{n}+\mathrm{1}} +{B}\:=\:{B}\:+\frac{\mathrm{3}{a}_{{n}} +\mathrm{1}}{\mathrm{2}}=\:\frac{\mathrm{3}{a}_{{n}} +\mathrm{2}{B}+\mathrm{1}}{\mathrm{2}} \\ $$$$\frac{{a}_{{n}+\mathrm{1}} +{A}}{{a}_{{n}+\mathrm{1}} +{B}}\:=\:\frac{\mathrm{3}{a}_{{n}} +\mathrm{2}{A}+\mathrm{1}}{\mathrm{3}{a}_{{n}} +\mathrm{2}{B}+\mathrm{1}} \\ $$$$\frac{{a}_{{n}+\mathrm{1}} +{A}}{{a}_{{n}+\mathrm{1}} +{B}}\:=\:\frac{\mathrm{3}}{\mathrm{3}}×\frac{{a}_{{n}} +\frac{\mathrm{2}{A}+\mathrm{1}}{\mathrm{3}}}{{a}_{{n}} +\frac{\mathrm{2}{B}+\mathrm{1}}{\mathrm{3}}} \\ $$$${A}=\:\frac{\mathrm{2}{A}+\mathrm{1}}{\mathrm{3}}\:\Rightarrow\:{A}=\mathrm{1} \\ $$$${B}\:=\:\mathrm{1}\:.\:{i}\:{have}\:{trouble} \\ $$
Commented by jagoll last updated on 16/Feb/20
$${hahaha}..{what}\:{wrong}\:{this}\:{my}\:{work}? \\ $$
Commented by mr W last updated on 16/Feb/20

$${the}\:{tactic}\:{with}\:{a}_{{n}+\mathrm{1}} +{A}\:{and}\:{a}_{{n}+\mathrm{1}} +{B} \\ $$$${is}\:{due}\:{to}\:{the}\:{fact}\:{that}\:{we}\:{have}\:{a}_{{n}} \:{in} \\ $$$${a}_{{n}+\mathrm{1}} =\frac{…{a}_{{n}} +….}{…{a}_{{n}} +…} \\ $$$${you}\:{can}\:{not}\:{apply}\:{this}\:{tactic}\:{for}\:{other} \\ $$$${cases}. \\ $$
Commented by jagoll last updated on 17/Feb/20
$${okay}\:{sir}\:{thank}\:{you} \\ $$
Answered by mr W last updated on 16/Feb/20
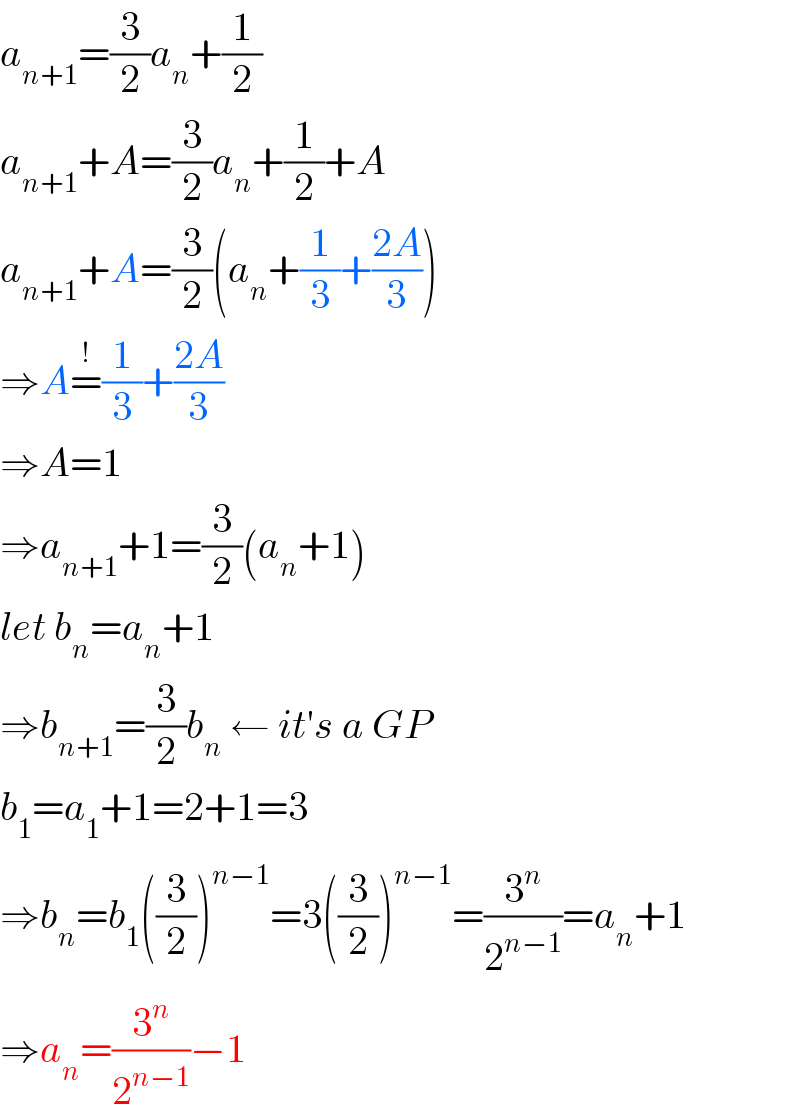
$${a}_{{n}+\mathrm{1}} =\frac{\mathrm{3}}{\mathrm{2}}{a}_{{n}} +\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${a}_{{n}+\mathrm{1}} +{A}=\frac{\mathrm{3}}{\mathrm{2}}{a}_{{n}} +\frac{\mathrm{1}}{\mathrm{2}}+{A} \\ $$$${a}_{{n}+\mathrm{1}} +{A}=\frac{\mathrm{3}}{\mathrm{2}}\left({a}_{{n}} +\frac{\mathrm{1}}{\mathrm{3}}+\frac{\mathrm{2}{A}}{\mathrm{3}}\right) \\ $$$$\Rightarrow{A}\overset{!} {=}\frac{\mathrm{1}}{\mathrm{3}}+\frac{\mathrm{2}{A}}{\mathrm{3}} \\ $$$$\Rightarrow{A}=\mathrm{1} \\ $$$$\Rightarrow{a}_{{n}+\mathrm{1}} +\mathrm{1}=\frac{\mathrm{3}}{\mathrm{2}}\left({a}_{{n}} +\mathrm{1}\right) \\ $$$${let}\:{b}_{{n}} ={a}_{{n}} +\mathrm{1} \\ $$$$\Rightarrow{b}_{{n}+\mathrm{1}} =\frac{\mathrm{3}}{\mathrm{2}}{b}_{{n}} \:\leftarrow\:{it}'{s}\:{a}\:{GP} \\ $$$${b}_{\mathrm{1}} ={a}_{\mathrm{1}} +\mathrm{1}=\mathrm{2}+\mathrm{1}=\mathrm{3} \\ $$$$\Rightarrow{b}_{{n}} ={b}_{\mathrm{1}} \left(\frac{\mathrm{3}}{\mathrm{2}}\right)^{{n}−\mathrm{1}} =\mathrm{3}\left(\frac{\mathrm{3}}{\mathrm{2}}\right)^{{n}−\mathrm{1}} =\frac{\mathrm{3}^{{n}} }{\mathrm{2}^{{n}−\mathrm{1}} }={a}_{{n}} +\mathrm{1} \\ $$$$\Rightarrow{a}_{{n}} =\frac{\mathrm{3}^{{n}} }{\mathrm{2}^{{n}−\mathrm{1}} }−\mathrm{1} \\ $$
