Question Number 81968 by mr W last updated on 17/Feb/20
Commented by mr W last updated on 17/Feb/20
![[derived from Q81804] given: string length =s (> 0.5L) friction coefficient with ground =μ to find: the minimal and maximal possible inclination of the rod and the corresponding tension in the string.](https://www.tinkutara.com/question/Q81969.png)
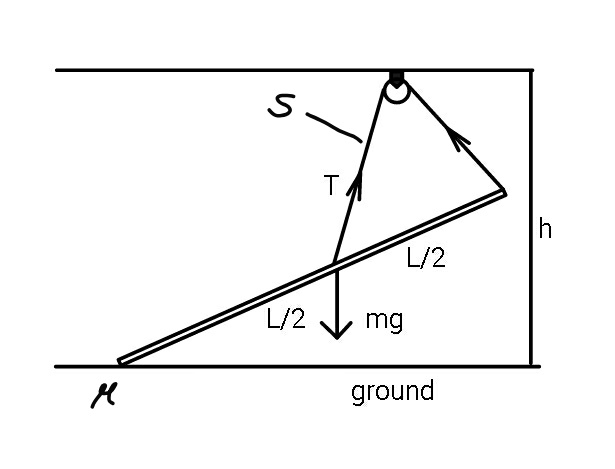
$$\left[{derived}\:{from}\:{Q}\mathrm{81804}\right] \\ $$$$ \\ $$$${given}: \\ $$$${string}\:{length}\:={s}\:\:\:\left(>\:\mathrm{0}.\mathrm{5}{L}\right) \\ $$$${friction}\:{coefficient}\:{with}\:{ground}\:=\mu \\ $$$$ \\ $$$${to}\:{find}: \\ $$$${the}\:{minimal}\:{and}\:{maximal}\:{possible} \\ $$$${inclination}\:{of}\:{the}\:{rod}\:{and}\:{the}\:\: \\ $$$${corresponding}\:{tension}\:{in}\:{the}\:{string}. \\ $$
Answered by mr W last updated on 27/Feb/20
Commented by mr W last updated on 27/Feb/20
)/(2 sin θ cos θ)) ⇒((4h)/L)=2 sin α+[cos (α−φ)+tan θ sin (α−φ)](((cos φ)/(tan θ))+sin φ) ⇒((4h)/L)=2 sin α+(cos Θ+tan θ sin Θ)[((cos (α−Θ))/(tan θ))+sin (α−Θ)] ...(ii) GC=BC×sin (θ−φ) GC=((L cos (θ−α+φ) sin (θ−φ))/(2 sin 2θ)) GC=((L [cos θ cos (α−φ)+sin θ sin (α−φ)] (sin θ cos φ−cos θ sin φ))/(4 sin θ cos θ)) GC=((L[cos (α−φ)+tan θ sin (α−φ)] (cos φ−((sin φ)/(tan θ))))/4) OG=((L cos α)/(2 tan ϕ))−h OG×tan φ=GC (((L cos α)/(2 tan ϕ))−h)tan φ=((L[cos (α−φ)+tan θ sin (α−φ)] (cos φ−((sin φ)/(tan θ))))/4) ⇒2(((cos α)/μ)−((2h)/L))tan φ=[cos (α−φ)+tan θ sin (α−φ)] (cos φ−((sin φ)/(tan θ))) ⇒2(((cos α)/μ)−((2h)/L))tan (α−Θ)=(cos Θ+tan θ sin Θ) [cos (α−Θ)−((sin (α−Θ))/(tan θ))] ...(iii) by putting (i) into (ii) and (iii) we get two equations for α and Θ. example: L=5m, h=3m, s=4m, μ=0.6 ⇒α=22.882° ⇒Θ=α−φ=7.0125°](https://www.tinkutara.com/question/Q83068.png)
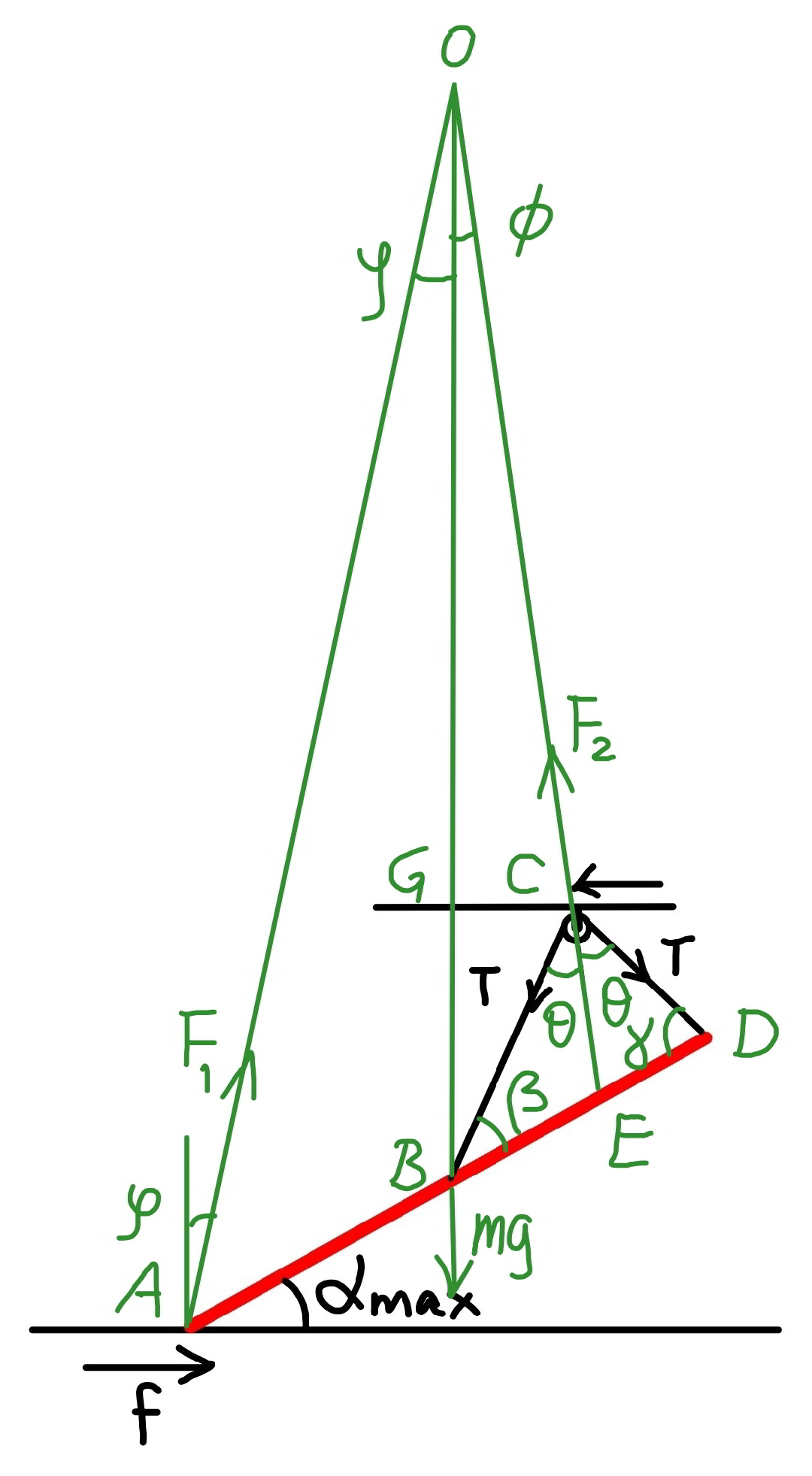
$${Case}\:{I}:\:{maximal}\:{inclination} \\ $$$${with}\:{friction}\:{force}\:{acting}\:{rightwards} \\ $$$$\varphi=\mathrm{tan}^{−\mathrm{1}} \mu \\ $$$${both}\:{reactions}\:{from}\:{ground}\:{and}\:{from} \\ $$$${pulley}\:{meet}\:{mg}\:{at}\:{the}\:{same}\:{point}\:{O}. \\ $$$$\beta=\frac{\pi}{\mathrm{2}}−\left(\theta+\alpha−\phi\right) \\ $$$$\gamma=\frac{\pi}{\mathrm{2}}−\left(\theta−\alpha+\phi\right) \\ $$$$\frac{{BC}}{\mathrm{sin}\:\gamma}=\frac{{CD}}{\mathrm{sin}\:\beta}=\frac{{BD}}{\mathrm{sin}\:\mathrm{2}\theta} \\ $$$$\Rightarrow{BC}=\frac{{L}\:\mathrm{cos}\:\left(\theta−\alpha+\phi\right)}{\mathrm{2}\:\mathrm{sin}\:\mathrm{2}\theta} \\ $$$$\Rightarrow{CD}=\frac{{L}\:\mathrm{cos}\:\left(\theta+\alpha−\phi\right)}{\mathrm{2}\:\mathrm{sin}\:\mathrm{2}\theta} \\ $$$${BC}+{CD}={s} \\ $$$$\Rightarrow\frac{{L}\:\mathrm{cos}\:\left(\theta−\alpha+\phi\right)}{\mathrm{2}\:\mathrm{sin}\:\mathrm{2}\theta}+\frac{{L}\:\mathrm{cos}\:\left(\theta+\alpha−\phi\right)}{\mathrm{2}\:\mathrm{sin}\:\mathrm{2}\theta}={s} \\ $$$$\Rightarrow{L}\:\mathrm{cos}\:\theta\:\mathrm{cos}\:\left(\alpha−\phi\right)={s}\:\mathrm{sin}\:\mathrm{2}\theta \\ $$$$\Rightarrow\mathrm{sin}\:\theta=\frac{{L}\:\mathrm{cos}\:\left(\alpha−\phi\right)}{\mathrm{2}{s}} \\ $$$${let}\:\Theta=\alpha−\phi \\ $$$$\Rightarrow\mathrm{sin}\:\theta=\frac{{L}\:\mathrm{cos}\:\Theta}{\mathrm{2}{s}}\:\:\:…\left({i}\right) \\ $$$$ \\ $$$${h}=\frac{{L}\:\mathrm{sin}\:\alpha}{\mathrm{2}}+{BC}×\mathrm{cos}\:\left(\theta−\phi\right) \\ $$$${h}=\frac{{L}\:\mathrm{sin}\:\alpha}{\mathrm{2}}+\frac{{L}\:\mathrm{cos}\:\left(\theta−\alpha+\phi\right)\:\mathrm{cos}\:\left(\theta−\phi\right)}{\mathrm{2}\:\mathrm{sin}\:\mathrm{2}\theta} \\ $$$$\frac{\mathrm{2}{h}}{{L}}=\mathrm{sin}\:\alpha+\frac{\mathrm{cos}\:\left(\theta−\alpha+\phi\right)\:\mathrm{cos}\:\left(\theta−\phi\right)}{\mathrm{sin}\:\mathrm{2}\theta} \\ $$$$\frac{\mathrm{2}{h}}{{L}}=\mathrm{sin}\:\alpha+\frac{\left[\mathrm{cos}\:\theta\:\mathrm{cos}\:\left(\alpha−\phi\right)+\mathrm{sin}\:\theta\:\mathrm{sin}\:\left(\alpha−\phi\right)\right]\left(\mathrm{cos}\:\theta\:\mathrm{cos}\:\phi+\mathrm{sin}\:\theta\:\mathrm{sin}\:\phi\right)}{\mathrm{2}\:\mathrm{sin}\:\theta\:\mathrm{cos}\:\theta} \\ $$$$\Rightarrow\frac{\mathrm{4}{h}}{{L}}=\mathrm{2}\:\mathrm{sin}\:\alpha+\left[\mathrm{cos}\:\left(\alpha−\phi\right)+\mathrm{tan}\:\theta\:\mathrm{sin}\:\left(\alpha−\phi\right)\right]\left(\frac{\mathrm{cos}\:\phi}{\mathrm{tan}\:\theta}+\mathrm{sin}\:\phi\right) \\ $$$$\Rightarrow\frac{\mathrm{4}{h}}{{L}}=\mathrm{2}\:\mathrm{sin}\:\alpha+\left(\mathrm{cos}\:\Theta+\mathrm{tan}\:\theta\:\mathrm{sin}\:\Theta\right)\left[\frac{\mathrm{cos}\:\left(\alpha−\Theta\right)}{\mathrm{tan}\:\theta}+\mathrm{sin}\:\left(\alpha−\Theta\right)\right]\:\:\:…\left({ii}\right) \\ $$$$ \\ $$$${GC}={BC}×\mathrm{sin}\:\left(\theta−\phi\right) \\ $$$${GC}=\frac{{L}\:\mathrm{cos}\:\left(\theta−\alpha+\phi\right)\:\mathrm{sin}\:\left(\theta−\phi\right)}{\mathrm{2}\:\mathrm{sin}\:\mathrm{2}\theta} \\ $$$${GC}=\frac{{L}\:\left[\mathrm{cos}\:\theta\:\mathrm{cos}\:\left(\alpha−\phi\right)+\mathrm{sin}\:\theta\:\mathrm{sin}\:\left(\alpha−\phi\right)\right]\:\left(\mathrm{sin}\:\theta\:\mathrm{cos}\:\phi−\mathrm{cos}\:\theta\:\mathrm{sin}\:\phi\right)}{\mathrm{4}\:\mathrm{sin}\:\theta\:\mathrm{cos}\:\theta} \\ $$$${GC}=\frac{{L}\left[\mathrm{cos}\:\left(\alpha−\phi\right)+\mathrm{tan}\:\theta\:\mathrm{sin}\:\left(\alpha−\phi\right)\right]\:\left(\mathrm{cos}\:\phi−\frac{\mathrm{sin}\:\phi}{\mathrm{tan}\:\theta}\right)}{\mathrm{4}} \\ $$$${OG}=\frac{{L}\:\mathrm{cos}\:\alpha}{\mathrm{2}\:\mathrm{tan}\:\varphi}−{h} \\ $$$${OG}×\mathrm{tan}\:\phi={GC} \\ $$$$\left(\frac{{L}\:\mathrm{cos}\:\alpha}{\mathrm{2}\:\mathrm{tan}\:\varphi}−{h}\right)\mathrm{tan}\:\phi=\frac{{L}\left[\mathrm{cos}\:\left(\alpha−\phi\right)+\mathrm{tan}\:\theta\:\mathrm{sin}\:\left(\alpha−\phi\right)\right]\:\left(\mathrm{cos}\:\phi−\frac{\mathrm{sin}\:\phi}{\mathrm{tan}\:\theta}\right)}{\mathrm{4}} \\ $$$$\Rightarrow\mathrm{2}\left(\frac{\mathrm{cos}\:\alpha}{\mu}−\frac{\mathrm{2}{h}}{{L}}\right)\mathrm{tan}\:\phi=\left[\mathrm{cos}\:\left(\alpha−\phi\right)+\mathrm{tan}\:\theta\:\mathrm{sin}\:\left(\alpha−\phi\right)\right]\:\left(\mathrm{cos}\:\phi−\frac{\mathrm{sin}\:\phi}{\mathrm{tan}\:\theta}\right) \\ $$$$\Rightarrow\mathrm{2}\left(\frac{\mathrm{cos}\:\alpha}{\mu}−\frac{\mathrm{2}{h}}{{L}}\right)\mathrm{tan}\:\left(\alpha−\Theta\right)=\left(\mathrm{cos}\:\Theta+\mathrm{tan}\:\theta\:\mathrm{sin}\:\Theta\right)\:\left[\mathrm{cos}\:\left(\alpha−\Theta\right)−\frac{\mathrm{sin}\:\left(\alpha−\Theta\right)}{\mathrm{tan}\:\theta}\right]\:\:\:…\left({iii}\right) \\ $$$${by}\:{putting}\:\left({i}\right)\:{into}\:\left({ii}\right)\:{and}\:\left({iii}\right)\:{we}\:{get} \\ $$$${two}\:{equations}\:{for}\:\alpha\:{and}\:\Theta. \\ $$$$ \\ $$$${example}: \\ $$$${L}=\mathrm{5}{m},\:{h}=\mathrm{3}{m},\:{s}=\mathrm{4}{m},\:\mu=\mathrm{0}.\mathrm{6} \\ $$$$\Rightarrow\alpha=\mathrm{22}.\mathrm{882}° \\ $$$$\Rightarrow\Theta=\alpha−\phi=\mathrm{7}.\mathrm{0125}° \\ $$
Commented by mr W last updated on 28/Feb/20
![((BC)/(sin (2θ+β)))=((CD)/(sin β))=(L/(2 sin 2θ)) BC=((L sin (2θ+β))/(2 sin 2θ)) CD=((L sin β)/(2 sin 2θ)) s=((L [sin 2θ cos β+(1+cos 2θ)sin β])/(2 sin 2θ)) ⇒((2s)/L)=cos β+(((1+cos 2θ)sin β)/(sin 2θ)) ⇒((2s)/L)×((sin 2θ)/( (√(2(1+cos 2θ)))))=sin λ cos β+cos λ sin β ⇒((2s)/L)×((sin 2θ)/( (√(2(1+cos 2θ)))))=sin (λ+β) ⇒β=sin^(−1) [((2s)/L)×((sin 2θ)/( (√(2(1+cos 2θ)))))]−tan^(−1) ((sin 2θ)/(1+cos 2θ)) h=((L sin α)/2)+BC×sin (β+α) ((2h)/L)=sin α+((sin (2θ+β) sin (β+α))/(sin 2θ)) ((2h)/L)=sin α+(cos β+((sin β)/(tan 2θ)))(sin β cos α+cos β sin α) ((2h)/L)=(1+cos^2 β+((sin β cos β)/(tan 2θ)))sin α+(sin β cos β+((sin^2 β)/(tan 2θ))) cos α ((2h)/L)×(1/( (√((1+cos^2 β+((sin β cos β)/(tan 2θ)))^2 +(sin β cos β+((sin^2 β)/(tan 2θ)))^2 ))))=cos δ sin α+sin δ cos α ((2h)/L)×(1/( (√((1+cos^2 β+((sin β cos β)/(tan 2θ)))^2 +(sin β cos β+((sin^2 β)/(tan 2θ)))^2 ))))= sin (α+δ) ⇒α=sin^(−1) [((2h)/L)×(1/( (√((1+cos^2 β+((sin β cos β)/(tan 2θ)))^2 +(sin β cos β+((sin^2 β)/(tan 2θ)))^2 ))))]−tan^(−1) [((sin β cos β+((sin^2 β)/(tan 2θ)))/(1+cos^2 β+((sin β cos β)/(tan 2θ))))] ⇒2(((cos α)/μ)−((2h)/L))tan φ=[cos (α−φ)+tan θ sin (α−φ)] (cos φ−((sin φ)/(tan θ))) φ=θ+α+β−(π/2) ⇒2(((cos α)/μ)−((2h)/L))(1/(tan (θ+α+β)))+[sin (θ+β)+tan θ cos (θ+β)] [sin (θ+α+β)+((cos (θ+α+β))/(tan θ))]=0](https://www.tinkutara.com/question/Q83111.png)
$$\frac{{BC}}{\mathrm{sin}\:\left(\mathrm{2}\theta+\beta\right)}=\frac{{CD}}{\mathrm{sin}\:\beta}=\frac{{L}}{\mathrm{2}\:\mathrm{sin}\:\mathrm{2}\theta} \\ $$$${BC}=\frac{{L}\:\mathrm{sin}\:\left(\mathrm{2}\theta+\beta\right)}{\mathrm{2}\:\mathrm{sin}\:\mathrm{2}\theta} \\ $$$${CD}=\frac{{L}\:\mathrm{sin}\:\beta}{\mathrm{2}\:\mathrm{sin}\:\mathrm{2}\theta} \\ $$$${s}=\frac{{L}\:\left[\mathrm{sin}\:\mathrm{2}\theta\:\mathrm{cos}\:\beta+\left(\mathrm{1}+\mathrm{cos}\:\mathrm{2}\theta\right)\mathrm{sin}\:\beta\right]}{\mathrm{2}\:\mathrm{sin}\:\mathrm{2}\theta} \\ $$$$\Rightarrow\frac{\mathrm{2}{s}}{{L}}=\mathrm{cos}\:\beta+\frac{\left(\mathrm{1}+\mathrm{cos}\:\mathrm{2}\theta\right)\mathrm{sin}\:\beta}{\mathrm{sin}\:\mathrm{2}\theta} \\ $$$$\Rightarrow\frac{\mathrm{2}{s}}{{L}}×\frac{\mathrm{sin}\:\mathrm{2}\theta}{\:\sqrt{\mathrm{2}\left(\mathrm{1}+\mathrm{cos}\:\mathrm{2}\theta\right)}}=\mathrm{sin}\:\lambda\:\mathrm{cos}\:\beta+\mathrm{cos}\:\lambda\:\mathrm{sin}\:\beta \\ $$$$\Rightarrow\frac{\mathrm{2}{s}}{{L}}×\frac{\mathrm{sin}\:\mathrm{2}\theta}{\:\sqrt{\mathrm{2}\left(\mathrm{1}+\mathrm{cos}\:\mathrm{2}\theta\right)}}=\mathrm{sin}\:\left(\lambda+\beta\right) \\ $$$$\Rightarrow\beta=\mathrm{sin}^{−\mathrm{1}} \left[\frac{\mathrm{2}{s}}{{L}}×\frac{\mathrm{sin}\:\mathrm{2}\theta}{\:\sqrt{\mathrm{2}\left(\mathrm{1}+\mathrm{cos}\:\mathrm{2}\theta\right)}}\right]−\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{sin}\:\mathrm{2}\theta}{\mathrm{1}+\mathrm{cos}\:\mathrm{2}\theta} \\ $$$$ \\ $$$${h}=\frac{{L}\:\mathrm{sin}\:\alpha}{\mathrm{2}}+{BC}×\mathrm{sin}\:\left(\beta+\alpha\right) \\ $$$$\frac{\mathrm{2}{h}}{{L}}=\mathrm{sin}\:\alpha+\frac{\mathrm{sin}\:\left(\mathrm{2}\theta+\beta\right)\:\mathrm{sin}\:\left(\beta+\alpha\right)}{\mathrm{sin}\:\mathrm{2}\theta} \\ $$$$\frac{\mathrm{2}{h}}{{L}}=\mathrm{sin}\:\alpha+\left(\mathrm{cos}\:\beta+\frac{\mathrm{sin}\:\beta}{\mathrm{tan}\:\mathrm{2}\theta}\right)\left(\mathrm{sin}\:\beta\:\mathrm{cos}\:\alpha+\mathrm{cos}\:\beta\:\mathrm{sin}\:\alpha\right) \\ $$$$\frac{\mathrm{2}{h}}{{L}}=\left(\mathrm{1}+\mathrm{cos}^{\mathrm{2}} \:\beta+\frac{\mathrm{sin}\:\beta\:\mathrm{cos}\:\beta}{\mathrm{tan}\:\mathrm{2}\theta}\right)\mathrm{sin}\:\alpha+\left(\mathrm{sin}\:\beta\:\mathrm{cos}\:\beta+\frac{\mathrm{sin}^{\mathrm{2}} \:\beta}{\mathrm{tan}\:\mathrm{2}\theta}\right)\:\mathrm{cos}\:\alpha \\ $$$$\frac{\mathrm{2}{h}}{{L}}×\frac{\mathrm{1}}{\:\sqrt{\left(\mathrm{1}+\mathrm{cos}^{\mathrm{2}} \:\beta+\frac{\mathrm{sin}\:\beta\:\mathrm{cos}\:\beta}{\mathrm{tan}\:\mathrm{2}\theta}\right)^{\mathrm{2}} +\left(\mathrm{sin}\:\beta\:\mathrm{cos}\:\beta+\frac{\mathrm{sin}^{\mathrm{2}} \:\beta}{\mathrm{tan}\:\mathrm{2}\theta}\right)^{\mathrm{2}} }}=\mathrm{cos}\:\delta\:\mathrm{sin}\:\alpha+\mathrm{sin}\:\delta\:\mathrm{cos}\:\alpha \\ $$$$\frac{\mathrm{2}{h}}{{L}}×\frac{\mathrm{1}}{\:\sqrt{\left(\mathrm{1}+\mathrm{cos}^{\mathrm{2}} \:\beta+\frac{\mathrm{sin}\:\beta\:\mathrm{cos}\:\beta}{\mathrm{tan}\:\mathrm{2}\theta}\right)^{\mathrm{2}} +\left(\mathrm{sin}\:\beta\:\mathrm{cos}\:\beta+\frac{\mathrm{sin}^{\mathrm{2}} \:\beta}{\mathrm{tan}\:\mathrm{2}\theta}\right)^{\mathrm{2}} }}=\:\mathrm{sin}\:\left(\alpha+\delta\right) \\ $$$$\Rightarrow\alpha=\mathrm{sin}^{−\mathrm{1}} \left[\frac{\mathrm{2}{h}}{{L}}×\frac{\mathrm{1}}{\:\sqrt{\left(\mathrm{1}+\mathrm{cos}^{\mathrm{2}} \:\beta+\frac{\mathrm{sin}\:\beta\:\mathrm{cos}\:\beta}{\mathrm{tan}\:\mathrm{2}\theta}\right)^{\mathrm{2}} +\left(\mathrm{sin}\:\beta\:\mathrm{cos}\:\beta+\frac{\mathrm{sin}^{\mathrm{2}} \:\beta}{\mathrm{tan}\:\mathrm{2}\theta}\right)^{\mathrm{2}} }}\right]−\mathrm{tan}^{−\mathrm{1}} \left[\frac{\mathrm{sin}\:\beta\:\mathrm{cos}\:\beta+\frac{\mathrm{sin}^{\mathrm{2}} \:\beta}{\mathrm{tan}\:\mathrm{2}\theta}}{\mathrm{1}+\mathrm{cos}^{\mathrm{2}} \:\beta+\frac{\mathrm{sin}\:\beta\:\mathrm{cos}\:\beta}{\mathrm{tan}\:\mathrm{2}\theta}}\right] \\ $$$$\Rightarrow\mathrm{2}\left(\frac{\mathrm{cos}\:\alpha}{\mu}−\frac{\mathrm{2}{h}}{{L}}\right)\mathrm{tan}\:\phi=\left[\mathrm{cos}\:\left(\alpha−\phi\right)+\mathrm{tan}\:\theta\:\mathrm{sin}\:\left(\alpha−\phi\right)\right]\:\left(\mathrm{cos}\:\phi−\frac{\mathrm{sin}\:\phi}{\mathrm{tan}\:\theta}\right) \\ $$$$\phi=\theta+\alpha+\beta−\frac{\pi}{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{2}\left(\frac{\mathrm{cos}\:\alpha}{\mu}−\frac{\mathrm{2}{h}}{{L}}\right)\frac{\mathrm{1}}{\mathrm{tan}\:\left(\theta+\alpha+\beta\right)}+\left[\mathrm{sin}\:\left(\theta+\beta\right)+\mathrm{tan}\:\theta\:\mathrm{cos}\:\left(\theta+\beta\right)\right]\:\left[\mathrm{sin}\:\left(\theta+\alpha+\beta\right)+\frac{\mathrm{cos}\:\left(\theta+\alpha+\beta\right)}{\mathrm{tan}\:\theta}\right]=\mathrm{0} \\ $$
Commented by ajfour last updated on 29/Feb/20

$$\mathrm{Even}\:\mathrm{with}\:\mathrm{your}\:\mathrm{solution}\:\mathrm{its}\:\mathrm{no} \\ $$$$\mathrm{simpler}\:\mathrm{sir}… \\ $$
Commented by mr W last updated on 29/Feb/20
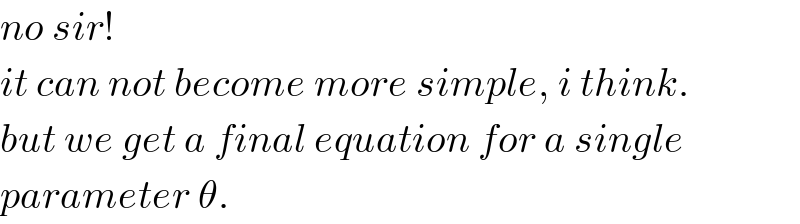
$${no}\:{sir}! \\ $$$${it}\:{can}\:{not}\:{become}\:{more}\:{simple},\:{i}\:{think}. \\ $$$${but}\:{we}\:{get}\:{a}\:{final}\:{equation}\:{for}\:{a}\:{single} \\ $$$${parameter}\:\theta. \\ $$
