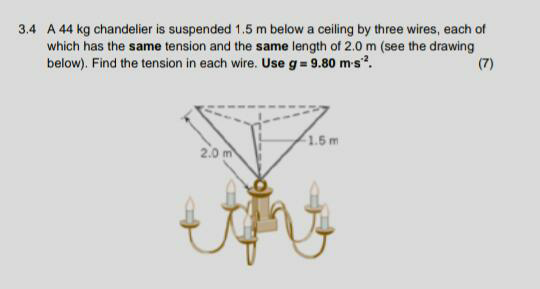
Question Number 81971 by TawaTawa last updated on 17/Feb/20
Answered by mind is power last updated on 17/Feb/20

$${angle}\:{between}\:{Wire}\:{and}\:{vertical}=\mathrm{cos}^{−\mathrm{1}} \left(\frac{\mathrm{1}.\mathrm{5}}{\mathrm{2}}\right)=\alpha \\ $$$${we}\:{get}\:\Sigma\overset{\rightarrow} {{F}}=\overset{\rightarrow} {\mathrm{0}} \\ $$$$\Rightarrow\overset{\rightarrow} {{T}}_{\mathrm{1}{y}} +\overset{\rightarrow} {{T}}_{\mathrm{2}{y}} +\overset{\rightarrow} {{T}}_{\mathrm{3}{y}} ={P}={m}\overset{\rightarrow} {{g}} \\ $$$${T}_{\mathrm{1}{y}} ={T}_{\mathrm{2}{y}} ={T}_{\mathrm{3}{y}} ={Tcos}\left(\alpha\right) \\ $$$$\Rightarrow\mathrm{3}{Tcos}\left(\alpha\right)={mg} \\ $$$$\left.{T}=\frac{{mg}}{\mathrm{3}{cos}\left(\alpha\right)}=\frac{\mathrm{44}.\mathrm{9}.\mathrm{81}}{\mathrm{3}.\frac{\mathrm{1}.\mathrm{5}}{\mathrm{2}}}=\frac{\mathrm{176}.\mathrm{9}.\mathrm{81}}{\mathrm{9}}=\left(\mathrm{1}.\mathrm{09}\right).\mathrm{176}\right)\sim\mathrm{193},\mathrm{6}{N} \\ $$
Commented by TawaTawa last updated on 17/Feb/20
$$\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir} \\ $$
