Menu Close

Question-81975

Tinku Tara 0 Comments
Pin




Question Number 81975 by TANMAY PANACEA last updated on 17/Feb/20
Commented by TANMAY PANACEA last updated on 17/Feb/20
thank you sir
$${thank}\:{you}\:{sir} \\ $$
Commented by mr W last updated on 17/Feb/20
please check your method sir! point (0,9) is wrong, should be (0, 7.5). point (6,6) is wrong, should be (5, 5). mininum 6+6(√2) is wrong, should be 6(√5).
$${please}\:{check}\:{your}\:{method}\:{sir}! \\ $$$${point}\:\left(\mathrm{0},\mathrm{9}\right)\:{is}\:{wrong},\:{should}\:{be}\:\left(\mathrm{0},\:\mathrm{7}.\mathrm{5}\right). \\ $$$${point}\:\left(\mathrm{6},\mathrm{6}\right)\:{is}\:{wrong},\:{should}\:{be}\:\left(\mathrm{5},\:\mathrm{5}\right). \\ $$$${mininum}\:\mathrm{6}+\mathrm{6}\sqrt{\mathrm{2}}\:{is}\:{wrong},\:{should}\:{be}\:\mathrm{6}\sqrt{\mathrm{5}}. \\ $$
Commented by jagoll last updated on 17/Feb/20
Commented by mr W last updated on 17/Feb/20
to santu sir: i think the error is that you assumed that the distance from (3,9) to the line y=x must be minimum. but this is not proved, and also not true.
$${to}\:{santu}\:{sir}: \\ $$$${i}\:{think}\:{the}\:{error}\:{is}\:{that}\:{you}\:{assumed} \\ $$$${that}\:{the}\:{distance}\:{from}\:\left(\mathrm{3},\mathrm{9}\right)\:{to}\:{the} \\ $$$${line}\:{y}={x}\:{must}\:{be}\:{minimum}.\:{but}\:{this} \\ $$$${is}\:{not}\:{proved},\:{and}\:{also}\:{not}\:{true}. \\ $$
Commented by john santu last updated on 17/Feb/20
haha, sorry there was work. yes sir , my method is invalid
$${haha},\:{sorry}\:{there}\:{was}\:{work}.\:{yes} \\ $$$${sir}\:,\:{my}\:{method}\:{is}\:{invalid} \\ $$
Answered by mr W last updated on 17/Feb/20
Commented by mr W last updated on 17/Feb/20
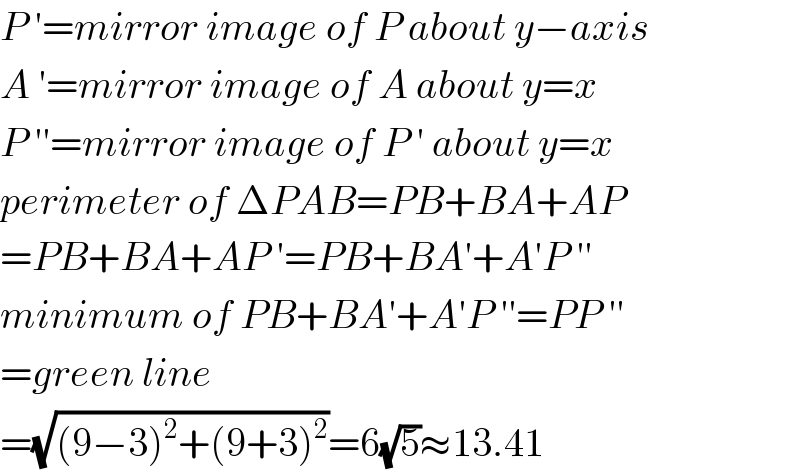
P ′=mirror image of P about y−axis A ′=mirror image of A about y=x P ′′=mirror image of P ′ about y=x perimeter of ΔPAB=PB+BA+AP =PB+BA+AP ′=PB+BA′+A′P ′′ minimum of PB+BA′+A′P ′′=PP ′′ =green line =(√((9−3)^2 +(9+3)^2 ))=6(√5)≈13.41
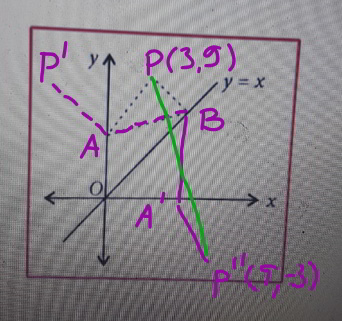
$${P}\:'={mirror}\:{image}\:{of}\:{P}\:{about}\:{y}−{axis} \\ $$$${A}\:'={mirror}\:{image}\:{of}\:{A}\:{about}\:{y}={x} \\ $$$${P}\:''={mirror}\:{image}\:{of}\:{P}\:'\:{about}\:{y}={x} \\ $$$${perimeter}\:{of}\:\Delta{PAB}={PB}+{BA}+{AP} \\ $$$$={PB}+{BA}+{AP}\:'={PB}+{BA}'+{A}'{P}\:'' \\ $$$${minimum}\:{of}\:{PB}+{BA}'+{A}'{P}\:''={PP}\:'' \\ $$$$={green}\:{line} \\ $$$$=\sqrt{\left(\mathrm{9}−\mathrm{3}\right)^{\mathrm{2}} +\left(\mathrm{9}+\mathrm{3}\right)^{\mathrm{2}} }=\mathrm{6}\sqrt{\mathrm{5}}\approx\mathrm{13}.\mathrm{41} \\ $$
Commented by TANMAY PANACEA last updated on 17/Feb/20
excellent sir...
$${excellent}\:{sir}… \\ $$
Commented by mr W last updated on 17/Feb/20
eqn. of PP ′′: ((y+3)/(9+3))=((x−9)/(3−9)) ⇒y=−2x+15 intersection with line y=x y_B =−2x_B +15=x_B ⇒x_B =5, y_B =5 ⇒point B(5,5) intersection with x−axis: y_(A′) =−2x_(A′) +15=0 ⇒x_(A′) =7.5 ⇒point A′ (7.5,0) ⇒point A(0,7.5)
$${eqn}.\:{of}\:{PP}\:'': \\ $$$$\frac{{y}+\mathrm{3}}{\mathrm{9}+\mathrm{3}}=\frac{{x}−\mathrm{9}}{\mathrm{3}−\mathrm{9}} \\ $$$$\Rightarrow{y}=−\mathrm{2}{x}+\mathrm{15} \\ $$$${intersection}\:{with}\:{line}\:{y}={x} \\ $$$${y}_{{B}} =−\mathrm{2}{x}_{{B}} +\mathrm{15}={x}_{{B}} \\ $$$$\Rightarrow{x}_{{B}} =\mathrm{5},\:{y}_{{B}} =\mathrm{5}\:\Rightarrow{point}\:{B}\left(\mathrm{5},\mathrm{5}\right) \\ $$$${intersection}\:{with}\:{x}−{axis}: \\ $$$${y}_{{A}'} =−\mathrm{2}{x}_{{A}'} +\mathrm{15}=\mathrm{0} \\ $$$$\Rightarrow{x}_{{A}'} =\mathrm{7}.\mathrm{5}\:\Rightarrow{point}\:{A}'\:\left(\mathrm{7}.\mathrm{5},\mathrm{0}\right) \\ $$$$\Rightarrow{point}\:{A}\left(\mathrm{0},\mathrm{7}.\mathrm{5}\right) \\ $$
Commented by mr W last updated on 17/Feb/20
i prefer such visiual solution...
$${i}\:{prefer}\:{such}\:{visiual}\:{solution}… \\ $$
Commented by john santu last updated on 17/Feb/20
point A (0, 7.5) wrong sir. the point is not on the line y = x . not accordance with problem
$${point}\:{A}\:\left(\mathrm{0},\:\mathrm{7}.\mathrm{5}\right)\:{wrong}\:{sir}.\: \\ $$$${the}\:{point}\:{is}\:{not}\:{on}\:{the}\:{line}\:{y}\:=\:{x} \\ $$$$.\:{not}\:{accordance}\:{with}\:{problem} \\ $$
Commented by mr W last updated on 17/Feb/20
calculus method: say A(0,a), B(b,b) perimeter =p p=(√(3^2 +(9−a)^2 ))+(√((3−b)^2 +(9−b)^2 ))+(√(b^2 +(b−a)^2 )) p=(√(90−18a+a^2 ))+(√(90−24b+2b^2 ))+(√(2b^2 −2ab+a^2 )) (∂p/∂a)=((−9+a)/( (√(90−18a+a^2 ))))+((−b+a)/( (√(2b^2 −2ab+a^2 ))))=0 ⇒((9−a)/( (√(90−18a+a^2 ))))=((a−b)/( (√(2b^2 −2ab+a^2 )))) ...(i) (∂p/∂b)=((−12+2b)/( (√(90−24b+2b^2 ))))+((2b−a)/( (√(2b^2 −2ab+a^2 ))))=0 ((12−2b)/( (√(90−24b+2b^2 ))))=((2b−a)/( (√(2b^2 −2ab+a^2 )))) ...(ii) from (i) and (ii) we get a=((15)/2), b=5. ⇒A(0,((15)/2)), B(5,5)
$${calculus}\:{method}: \\ $$$${say}\:{A}\left(\mathrm{0},{a}\right),\:{B}\left({b},{b}\right) \\ $$$${perimeter}\:={p} \\ $$$${p}=\sqrt{\mathrm{3}^{\mathrm{2}} +\left(\mathrm{9}−{a}\right)^{\mathrm{2}} }+\sqrt{\left(\mathrm{3}−{b}\right)^{\mathrm{2}} +\left(\mathrm{9}−{b}\right)^{\mathrm{2}} }+\sqrt{{b}^{\mathrm{2}} +\left({b}−{a}\right)^{\mathrm{2}} } \\ $$$${p}=\sqrt{\mathrm{90}−\mathrm{18}{a}+{a}^{\mathrm{2}} }+\sqrt{\mathrm{90}−\mathrm{24}{b}+\mathrm{2}{b}^{\mathrm{2}} }+\sqrt{\mathrm{2}{b}^{\mathrm{2}} −\mathrm{2}{ab}+{a}^{\mathrm{2}} } \\ $$$$\frac{\partial{p}}{\partial{a}}=\frac{−\mathrm{9}+{a}}{\:\sqrt{\mathrm{90}−\mathrm{18}{a}+{a}^{\mathrm{2}} }}+\frac{−{b}+{a}}{\:\sqrt{\mathrm{2}{b}^{\mathrm{2}} −\mathrm{2}{ab}+{a}^{\mathrm{2}} }}=\mathrm{0} \\ $$$$\Rightarrow\frac{\mathrm{9}−{a}}{\:\sqrt{\mathrm{90}−\mathrm{18}{a}+{a}^{\mathrm{2}} }}=\frac{{a}−{b}}{\:\sqrt{\mathrm{2}{b}^{\mathrm{2}} −\mathrm{2}{ab}+{a}^{\mathrm{2}} }}\:\:\:…\left({i}\right) \\ $$$$\frac{\partial{p}}{\partial{b}}=\frac{−\mathrm{12}+\mathrm{2}{b}}{\:\sqrt{\mathrm{90}−\mathrm{24}{b}+\mathrm{2}{b}^{\mathrm{2}} }}+\frac{\mathrm{2}{b}−{a}}{\:\sqrt{\mathrm{2}{b}^{\mathrm{2}} −\mathrm{2}{ab}+{a}^{\mathrm{2}} }}=\mathrm{0} \\ $$$$\frac{\mathrm{12}−\mathrm{2}{b}}{\:\sqrt{\mathrm{90}−\mathrm{24}{b}+\mathrm{2}{b}^{\mathrm{2}} }}=\frac{\mathrm{2}{b}−{a}}{\:\sqrt{\mathrm{2}{b}^{\mathrm{2}} −\mathrm{2}{ab}+{a}^{\mathrm{2}} }}\:\:\:…\left({ii}\right) \\ $$$$ \\ $$$${from}\:\left({i}\right)\:{and}\:\left({ii}\right)\:{we}\:{get}\:{a}=\frac{\mathrm{15}}{\mathrm{2}},\:{b}=\mathrm{5}. \\ $$$$\Rightarrow{A}\left(\mathrm{0},\frac{\mathrm{15}}{\mathrm{2}}\right),\:{B}\left(\mathrm{5},\mathrm{5}\right) \\ $$
Commented by mr W last updated on 17/Feb/20
santu sir: please check your comment again. look carefully at the picture: on the line y=x is the point B(5,5) and on y−axis is the point A(0, 7.5). what is wrong?
$${santu}\:{sir}: \\ $$$${please}\:{check}\:{your}\:{comment}\:{again}. \\ $$$${look}\:{carefully}\:{at}\:{the}\:{picture}: \\ $$$${on}\:{the}\:{line}\:{y}={x}\:{is}\:{the}\:{point}\:{B}\left(\mathrm{5},\mathrm{5}\right)\:{and} \\ $$$${on}\:{y}−{axis}\:{is}\:{the}\:{point}\:{A}\left(\mathrm{0},\:\mathrm{7}.\mathrm{5}\right). \\ $$$${what}\:{is}\:{wrong}? \\ $$
Answered by ajfour last updated on 17/Feb/20
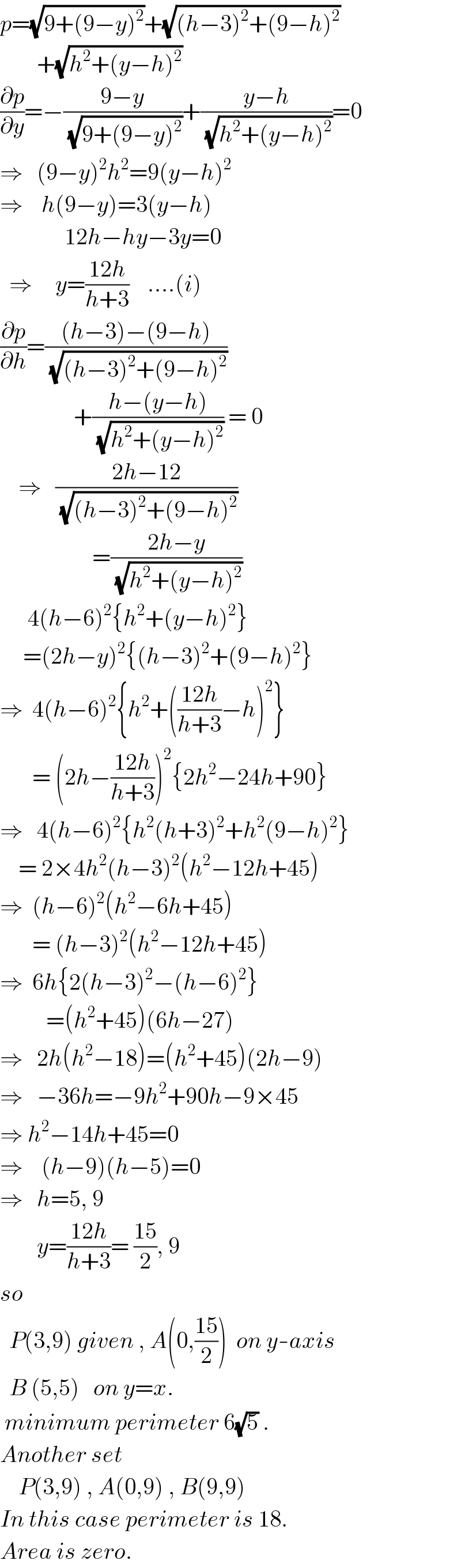
p=(√(9+(9−y)^2 ))+(√((h−3)^2 +(9−h)^2 )) +(√(h^2 +(y−h)^2 )) (∂p/∂y)=−((9−y)/( (√(9+(9−y)^2 ))))+((y−h)/( (√(h^2 +(y−h)^2 ))))=0 ⇒ (9−y)^2 h^2 =9(y−h)^2 ⇒ h(9−y)=3(y−h) 12h−hy−3y=0 ⇒ y=((12h)/(h+3)) ....(i) (∂p/∂h)=(((h−3)−(9−h))/( (√((h−3)^2 +(9−h)^2 )))) +((h−(y−h))/( (√(h^2 +(y−h)^2 )))) = 0 ⇒ ((2h−12)/( (√((h−3)^2 +(9−h)^2 )))) =((2h−y)/( (√(h^2 +(y−h)^2 )))) 4(h−6)^2 {h^2 +(y−h)^2 } =(2h−y)^2 {(h−3)^2 +(9−h)^2 } ⇒ 4(h−6)^2 {h^2 +(((12h)/(h+3))−h)^2 } = (2h−((12h)/(h+3)))^2 {2h^2 −24h+90} ⇒ 4(h−6)^2 {h^2 (h+3)^2 +h^2 (9−h)^2 } = 2×4h^2 (h−3)^2 (h^2 −12h+45) ⇒ (h−6)^2 (h^2 −6h+45) = (h−3)^2 (h^2 −12h+45) ⇒ 6h{2(h−3)^2 −(h−6)^2 } =(h^2 +45)(6h−27) ⇒ 2h(h^2 −18)=(h^2 +45)(2h−9) ⇒ −36h=−9h^2 +90h−9×45 ⇒ h^2 −14h+45=0 ⇒ (h−9)(h−5)=0 ⇒ h=5, 9 y=((12h)/(h+3))= ((15)/2), 9 so P(3,9) given , A(0,((15)/2)) on y-axis B (5,5) on y=x. minimum perimeter 6(√5) . Another set P(3,9) , A(0,9) , B(9,9) In this case perimeter is 18. Area is zero.
$${p}=\sqrt{\mathrm{9}+\left(\mathrm{9}−{y}\right)^{\mathrm{2}} }+\sqrt{\left({h}−\mathrm{3}\right)^{\mathrm{2}} +\left(\mathrm{9}−{h}\right)^{\mathrm{2}} } \\ $$$$\:\:\:\:\:\:\:\:+\sqrt{{h}^{\mathrm{2}} +\left({y}−{h}\right)^{\mathrm{2}} } \\ $$$$\frac{\partial{p}}{\partial{y}}=−\frac{\mathrm{9}−{y}}{\:\sqrt{\mathrm{9}+\left(\mathrm{9}−{y}\right)^{\mathrm{2}} }}+\frac{{y}−{h}}{\:\sqrt{{h}^{\mathrm{2}} +\left({y}−{h}\right)^{\mathrm{2}} }}=\mathrm{0} \\ $$$$\Rightarrow\:\:\:\left(\mathrm{9}−{y}\right)^{\mathrm{2}} {h}^{\mathrm{2}} =\mathrm{9}\left({y}−{h}\right)^{\mathrm{2}} \\ $$$$\Rightarrow\:\:\:\:{h}\left(\mathrm{9}−{y}\right)=\mathrm{3}\left({y}−{h}\right) \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{12}{h}−{hy}−\mathrm{3}{y}=\mathrm{0} \\ $$$$\:\:\Rightarrow\:\:\:\:\:{y}=\frac{\mathrm{12}{h}}{{h}+\mathrm{3}}\:\:\:\:….\left({i}\right) \\ $$$$\frac{\partial{p}}{\partial{h}}=\frac{\left({h}−\mathrm{3}\right)−\left(\mathrm{9}−{h}\right)}{\:\sqrt{\left({h}−\mathrm{3}\right)^{\mathrm{2}} +\left(\mathrm{9}−{h}\right)^{\mathrm{2}} }} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:+\frac{{h}−\left({y}−{h}\right)}{\:\sqrt{{h}^{\mathrm{2}} +\left({y}−{h}\right)^{\mathrm{2}} }}\:=\:\mathrm{0} \\ $$$$\:\:\:\:\Rightarrow\:\:\:\frac{\mathrm{2}{h}−\mathrm{12}}{\:\sqrt{\left({h}−\mathrm{3}\right)^{\mathrm{2}} +\left(\mathrm{9}−{h}\right)^{\mathrm{2}} }} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{\mathrm{2}{h}−{y}}{\:\sqrt{{h}^{\mathrm{2}} +\left({y}−{h}\right)^{\mathrm{2}} }} \\ $$$$\:\:\:\:\:\:\mathrm{4}\left({h}−\mathrm{6}\right)^{\mathrm{2}} \left\{{h}^{\mathrm{2}} +\left({y}−{h}\right)^{\mathrm{2}} \right\} \\ $$$$\:\:\:\:\:=\left(\mathrm{2}{h}−{y}\right)^{\mathrm{2}} \left\{\left({h}−\mathrm{3}\right)^{\mathrm{2}} +\left(\mathrm{9}−{h}\right)^{\mathrm{2}} \right\} \\ $$$$\Rightarrow\:\:\mathrm{4}\left({h}−\mathrm{6}\right)^{\mathrm{2}} \left\{{h}^{\mathrm{2}} +\left(\frac{\mathrm{12}{h}}{{h}+\mathrm{3}}−{h}\right)^{\mathrm{2}} \right\} \\ $$$$\:\:\:\:\:\:\:=\:\left(\mathrm{2}{h}−\frac{\mathrm{12}{h}}{{h}+\mathrm{3}}\right)^{\mathrm{2}} \left\{\mathrm{2}{h}^{\mathrm{2}} −\mathrm{24}{h}+\mathrm{90}\right\} \\ $$$$\Rightarrow\:\:\:\mathrm{4}\left({h}−\mathrm{6}\right)^{\mathrm{2}} \left\{{h}^{\mathrm{2}} \left({h}+\mathrm{3}\right)^{\mathrm{2}} +{h}^{\mathrm{2}} \left(\mathrm{9}−{h}\right)^{\mathrm{2}} \right\} \\ $$$$\:\:\:\:=\:\mathrm{2}×\mathrm{4}{h}^{\mathrm{2}} \left({h}−\mathrm{3}\right)^{\mathrm{2}} \left({h}^{\mathrm{2}} −\mathrm{12}{h}+\mathrm{45}\right) \\ $$$$\Rightarrow\:\:\left({h}−\mathrm{6}\right)^{\mathrm{2}} \left({h}^{\mathrm{2}} −\mathrm{6}{h}+\mathrm{45}\right) \\ $$$$\:\:\:\:\:\:\:=\:\left({h}−\mathrm{3}\right)^{\mathrm{2}} \left({h}^{\mathrm{2}} −\mathrm{12}{h}+\mathrm{45}\right) \\ $$$$\Rightarrow\:\:\mathrm{6}{h}\left\{\mathrm{2}\left({h}−\mathrm{3}\right)^{\mathrm{2}} −\left({h}−\mathrm{6}\right)^{\mathrm{2}} \right\} \\ $$$$\:\:\:\:\:\:\:\:\:\:=\left({h}^{\mathrm{2}} +\mathrm{45}\right)\left(\mathrm{6}{h}−\mathrm{27}\right) \\ $$$$\Rightarrow\:\:\:\mathrm{2}{h}\left({h}^{\mathrm{2}} −\mathrm{18}\right)=\left({h}^{\mathrm{2}} +\mathrm{45}\right)\left(\mathrm{2}{h}−\mathrm{9}\right) \\ $$$$\Rightarrow\:\:\:−\mathrm{36}{h}=−\mathrm{9}{h}^{\mathrm{2}} +\mathrm{90}{h}−\mathrm{9}×\mathrm{45} \\ $$$$\Rightarrow\:{h}^{\mathrm{2}} −\mathrm{14}{h}+\mathrm{45}=\mathrm{0} \\ $$$$\Rightarrow\:\:\:\:\left({h}−\mathrm{9}\right)\left({h}−\mathrm{5}\right)=\mathrm{0} \\ $$$$\Rightarrow\:\:\:{h}=\mathrm{5},\:\mathrm{9} \\ $$$$\:\:\:\:\:\:\:\:{y}=\frac{\mathrm{12}{h}}{{h}+\mathrm{3}}=\:\frac{\mathrm{15}}{\mathrm{2}},\:\mathrm{9} \\ $$$${so} \\ $$$$\:\:{P}\left(\mathrm{3},\mathrm{9}\right)\:{given}\:,\:{A}\left(\mathrm{0},\frac{\mathrm{15}}{\mathrm{2}}\right)\:\:{on}\:{y}-{axis} \\ $$$$\:\:{B}\:\left(\mathrm{5},\mathrm{5}\right)\:\:\:{on}\:{y}={x}.\:\: \\ $$$$\:{minimum}\:{perimeter}\:\mathrm{6}\sqrt{\mathrm{5}}\:. \\ $$$${Another}\:{set} \\ $$$$\:\:\:\:{P}\left(\mathrm{3},\mathrm{9}\right)\:,\:{A}\left(\mathrm{0},\mathrm{9}\right)\:,\:{B}\left(\mathrm{9},\mathrm{9}\right) \\ $$$${In}\:{this}\:{case}\:{perimeter}\:{is}\:\mathrm{18}. \\ $$$${Area}\:{is}\:{zero}. \\ $$
Commented by mr W last updated on 17/Feb/20
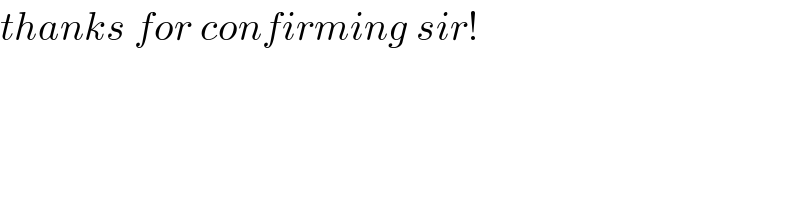
thanks for confirming sir!
$${thanks}\:{for}\:{confirming}\:{sir}! \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *