Question Number 81980 by Hassen_Timol last updated on 17/Feb/20
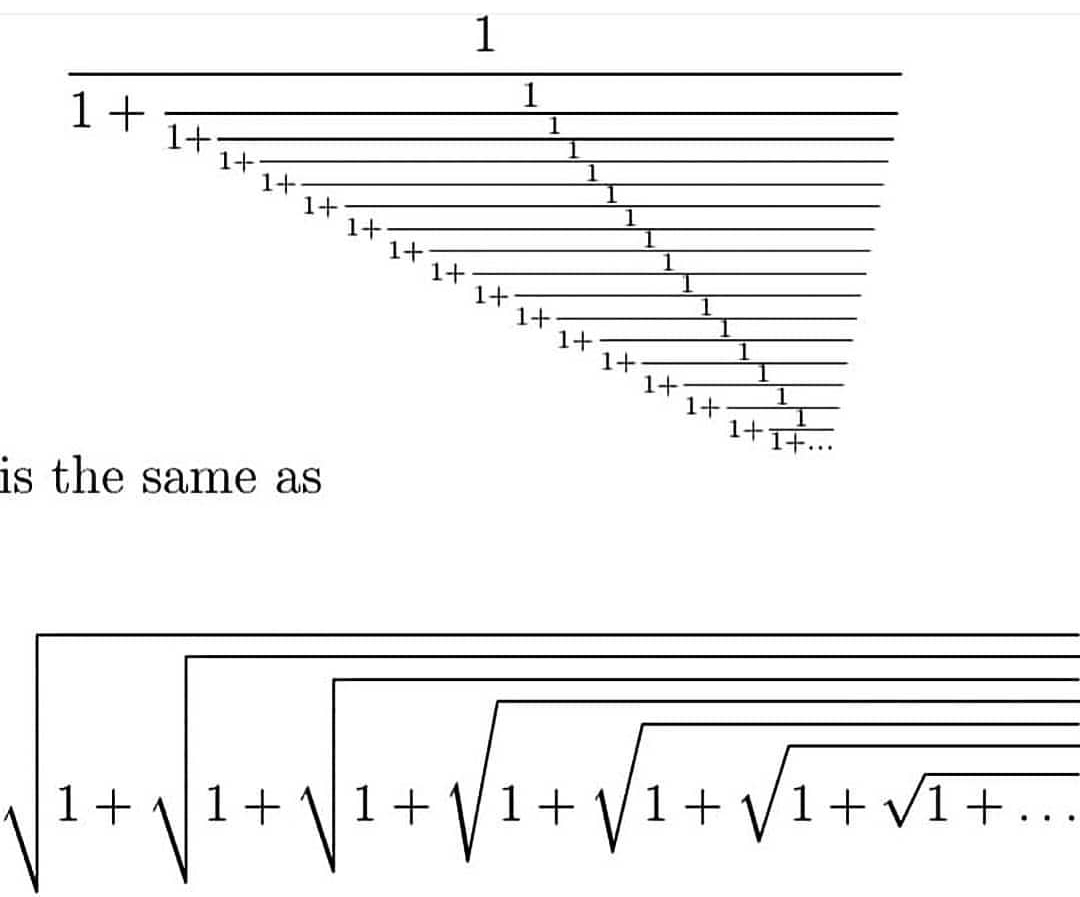
Commented by Hassen_Timol last updated on 17/Feb/20
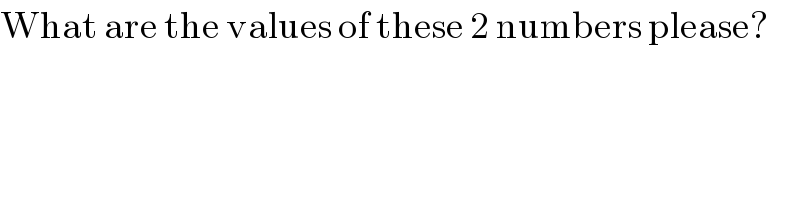
$$\mathrm{What}\:\mathrm{are}\:\mathrm{the}\:\mathrm{values}\:\mathrm{of}\:\mathrm{these}\:\mathrm{2}\:\mathrm{numbers}\:\mathrm{please}? \\ $$
Commented by Hassen_Timol last updated on 17/Feb/20
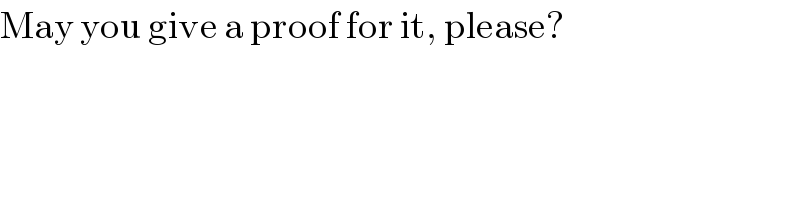
$$\mathrm{May}\:\mathrm{you}\:\mathrm{give}\:\mathrm{a}\:\mathrm{proof}\:\mathrm{for}\:\mathrm{it},\:\mathrm{please}? \\ $$
Answered by $@ty@m123 last updated on 17/Feb/20
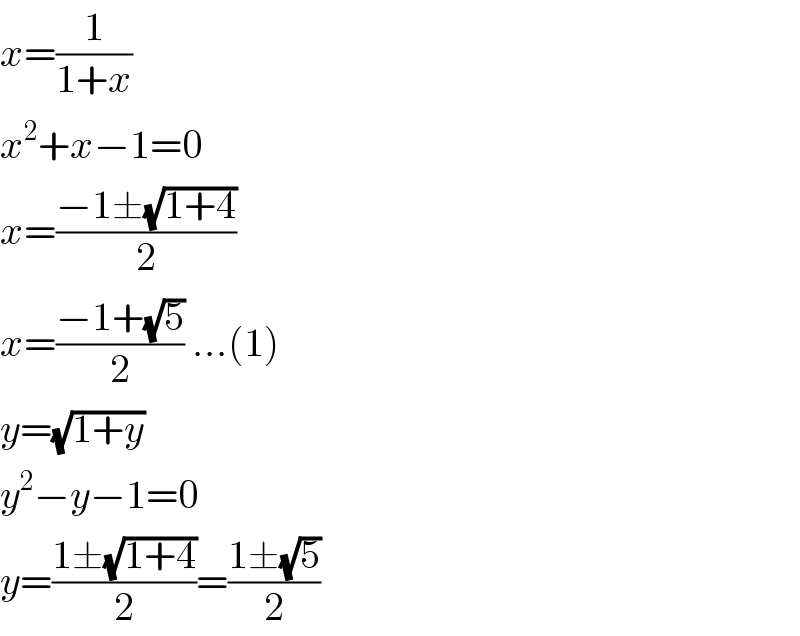
$${x}=\frac{\mathrm{1}}{\mathrm{1}+{x}} \\ $$$${x}^{\mathrm{2}} +{x}−\mathrm{1}=\mathrm{0} \\ $$$${x}=\frac{−\mathrm{1}\pm\sqrt{\mathrm{1}+\mathrm{4}}}{\mathrm{2}} \\ $$$${x}=\frac{−\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}\:…\left(\mathrm{1}\right) \\ $$$${y}=\sqrt{\mathrm{1}+{y}} \\ $$$${y}^{\mathrm{2}} −{y}−\mathrm{1}=\mathrm{0} \\ $$$${y}=\frac{\mathrm{1}\pm\sqrt{\mathrm{1}+\mathrm{4}}}{\mathrm{2}}=\frac{\mathrm{1}\pm\sqrt{\mathrm{5}}}{\mathrm{2}} \\ $$
Commented by mr W last updated on 17/Feb/20
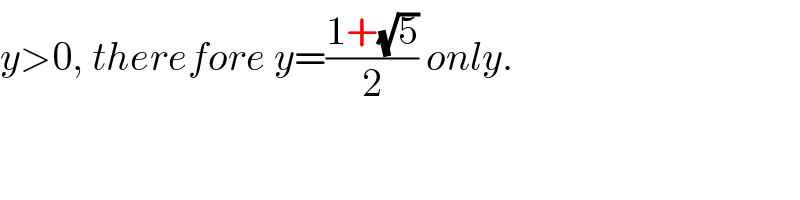
$${y}>\mathrm{0},\:{therefore}\:{y}=\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}\:{only}. \\ $$
Commented by Hassen_Timol last updated on 17/Feb/20
$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{very}\:\mathrm{much}!!! \\ $$
