Question Number 82084 by oyemi kemewari last updated on 18/Feb/20
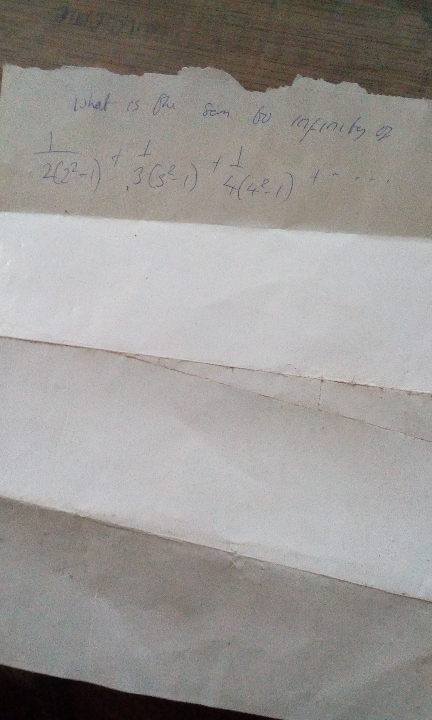
Commented by john santu last updated on 18/Feb/20
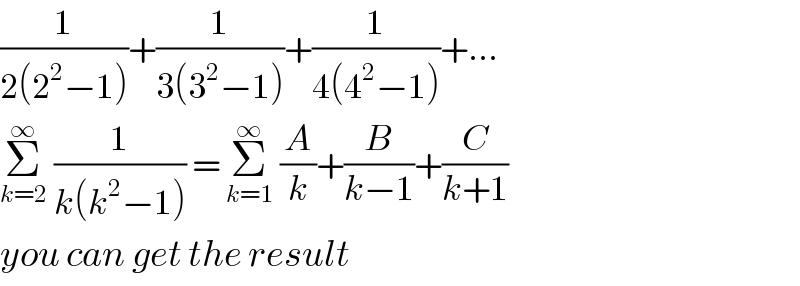
$$\frac{\mathrm{1}}{\mathrm{2}\left(\mathrm{2}^{\mathrm{2}} −\mathrm{1}\right)}+\frac{\mathrm{1}}{\mathrm{3}\left(\mathrm{3}^{\mathrm{2}} −\mathrm{1}\right)}+\frac{\mathrm{1}}{\mathrm{4}\left(\mathrm{4}^{\mathrm{2}} −\mathrm{1}\right)}+… \\ $$$$\underset{{k}=\mathrm{2}} {\overset{\infty} {\sum}}\:\frac{\mathrm{1}}{{k}\left({k}^{\mathrm{2}} −\mathrm{1}\right)}\:=\:\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\:\frac{{A}}{{k}}+\frac{{B}}{{k}−\mathrm{1}}+\frac{{C}}{{k}+\mathrm{1}} \\ $$$${you}\:{can}\:{get}\:{the}\:{result} \\ $$
Commented by john santu last updated on 18/Feb/20
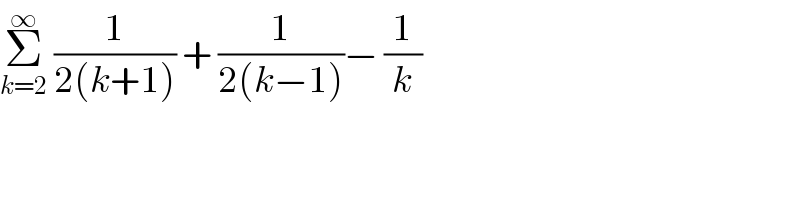
$$\underset{{k}=\mathrm{2}} {\overset{\infty} {\sum}}\:\frac{\mathrm{1}}{\mathrm{2}\left({k}+\mathrm{1}\right)}\:+\:\frac{\mathrm{1}}{\mathrm{2}\left({k}−\mathrm{1}\right)}−\:\frac{\mathrm{1}}{{k}} \\ $$
