Question Number 82125 by liki last updated on 18/Feb/20

Commented by john santu last updated on 18/Feb/20
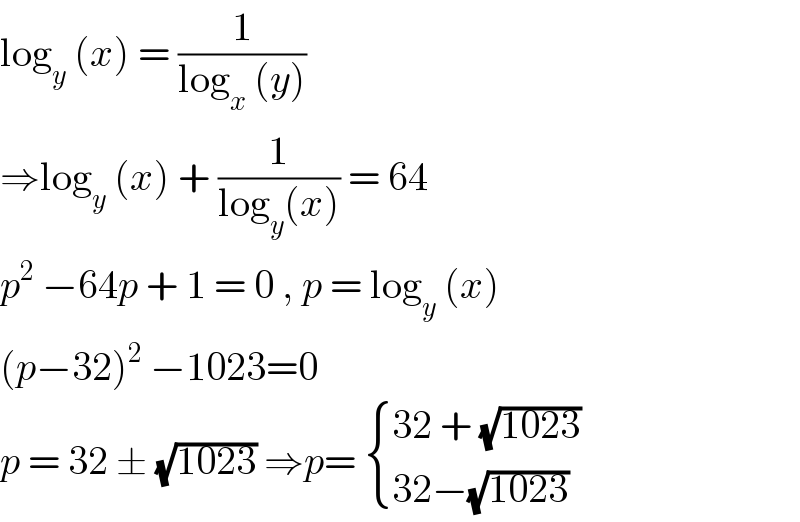
$$\mathrm{log}_{{y}} \:\left({x}\right)\:=\:\frac{\mathrm{1}}{\mathrm{log}_{{x}} \:\left({y}\right)} \\ $$$$\Rightarrow\mathrm{log}_{{y}} \:\left({x}\right)\:+\:\frac{\mathrm{1}}{\mathrm{log}_{{y}} \left({x}\right)}\:=\:\mathrm{64} \\ $$$${p}^{\mathrm{2}} \:−\mathrm{64}{p}\:+\:\mathrm{1}\:=\:\mathrm{0}\:,\:{p}\:=\:\mathrm{log}_{{y}} \:\left({x}\right) \\ $$$$\left({p}−\mathrm{32}\right)^{\mathrm{2}} \:−\mathrm{1023}=\mathrm{0} \\ $$$${p}\:=\:\mathrm{32}\:\pm\:\sqrt{\mathrm{1023}}\:\Rightarrow{p}=\:\begin{cases}{\mathrm{32}\:+\:\sqrt{\mathrm{1023}}}\\{\mathrm{32}−\sqrt{\mathrm{1023}}}\end{cases} \\ $$
Commented by liki last updated on 18/Feb/20

$$..\boldsymbol{{help}}\:\boldsymbol{{me}}\:\boldsymbol{{plz}}… \\ $$
Commented by liki last updated on 18/Feb/20
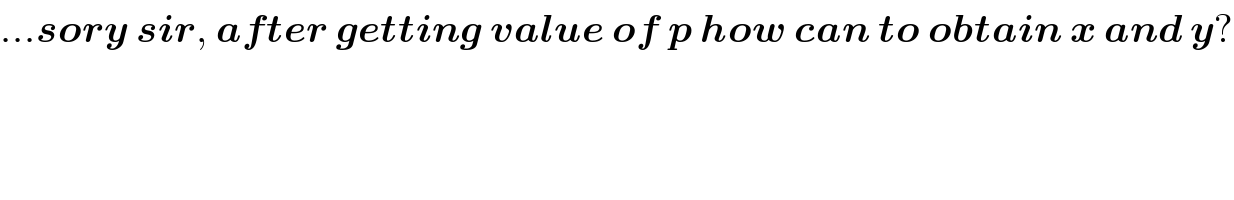
$$…\boldsymbol{{sory}}\:\boldsymbol{{sir}},\:\boldsymbol{{after}}\:\boldsymbol{{getting}}\:\boldsymbol{{value}}\:\boldsymbol{{of}}\:\boldsymbol{{p}}\:\boldsymbol{{how}}\:\boldsymbol{{can}}\:\boldsymbol{{to}}\:\boldsymbol{{obtain}}\:\boldsymbol{{x}}\:\boldsymbol{{and}}\:\boldsymbol{{y}}? \\ $$
Commented by liki last updated on 18/Feb/20
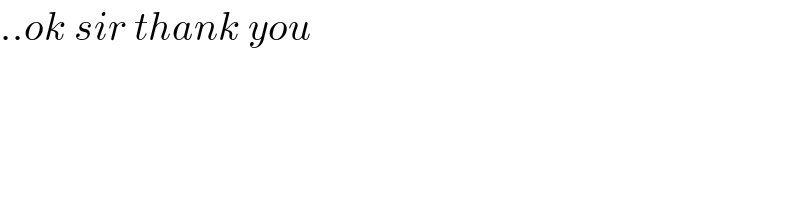
$$..{ok}\:{sir}\:{thank}\:{you} \\ $$
Commented by mr W last updated on 18/Feb/20

$${you}\:{have}\:{two}\:{unknowns}\:{x},\:{y} \\ $$$${but}\:{you}\:{have}\:{only}\:{one}\:{equation},\:{in} \\ $$$${this}\:{case}\:{you}\:{can}\:{not}\:{determine}\:{x} \\ $$$${and}\:{y}!\:{because}\:{there}\:{are}\:{infinite} \\ $$$${possibilities}. \\ $$
