Question Number 82134 by Raxreedoroid last updated on 18/Feb/20

Commented by Raxreedoroid last updated on 18/Feb/20
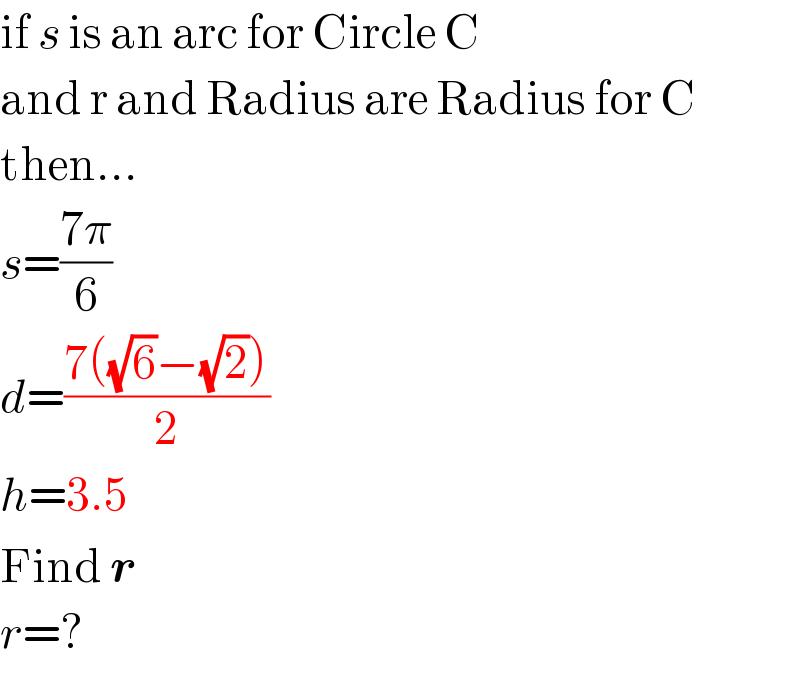
$$\mathrm{if}\:{s}\:\mathrm{is}\:\mathrm{an}\:\mathrm{arc}\:\mathrm{for}\:\mathrm{Circle}\:\mathrm{C} \\ $$$$\mathrm{and}\:\mathrm{r}\:\mathrm{and}\:\mathrm{Radius}\:\mathrm{are}\:\mathrm{Radius}\:\mathrm{for}\:\mathrm{C} \\ $$$$\mathrm{then}… \\ $$$${s}=\frac{\mathrm{7}\pi}{\mathrm{6}} \\ $$$${d}=\frac{\mathrm{7}\left(\sqrt{\mathrm{6}}−\sqrt{\mathrm{2}}\right)}{\mathrm{2}} \\ $$$${h}=\mathrm{3}.\mathrm{5} \\ $$$$\mathrm{Find}\:\boldsymbol{{r}} \\ $$$${r}=? \\ $$
Commented by mr W last updated on 18/Feb/20

$${your}\:{question}\:{is}\:{wrong}\:{sir}! \\ $$$${you}\:{should}\:{know}\:{and}\:{see}\:{that} \\ $$$${s}>{d}>{h} \\ $$$$ \\ $$$${but}\:{you}\:{have} \\ $$$${s}=\frac{\mathrm{7}\pi}{\mathrm{6}}\approx\mathrm{3}.\mathrm{665} \\ $$$${d}=\mathrm{4} \\ $$$${h}=\sqrt{\mathrm{6}}+\sqrt{\mathrm{2}}\approx\mathrm{3}.\mathrm{864} \\ $$$${i}.{e}.\:{d}>{h}\overset{!} {>}{s}\:\Rightarrow\:{this}\:{is}\:{impossible}! \\ $$
Commented by Raxreedoroid last updated on 18/Feb/20

$$\mathrm{sorry}!\:\mathrm{Here}\:\mathrm{I}\:\mathrm{edited}\:\mathrm{the}\:\mathrm{values}. \\ $$
Commented by mr W last updated on 18/Feb/20
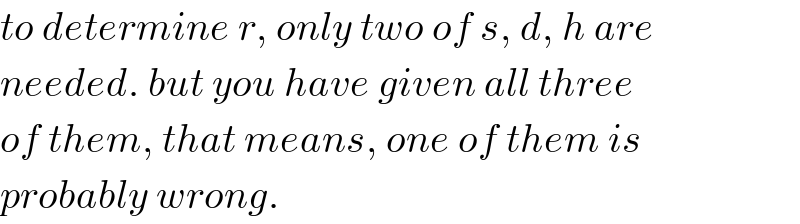
$${to}\:{determine}\:{r},\:{only}\:{two}\:{of}\:{s},\:{d},\:{h}\:{are} \\ $$$${needed}.\:{but}\:{you}\:{have}\:{given}\:{all}\:{three} \\ $$$${of}\:{them},\:{that}\:{means},\:{one}\:{of}\:{them}\:{is}\: \\ $$$${probably}\:{wrong}. \\ $$
Commented by Raxreedoroid last updated on 19/Feb/20
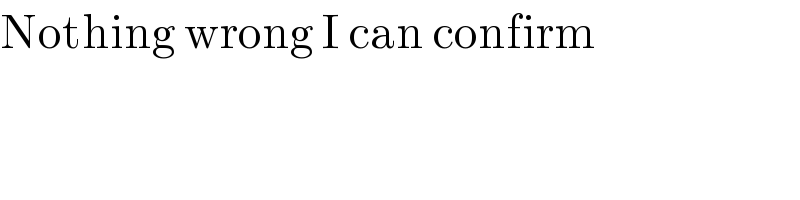
$$\mathrm{Nothing}\:\mathrm{wrong}\:\mathrm{I}\:\mathrm{can}\:\mathrm{confirm} \\ $$
Commented by mr W last updated on 19/Feb/20
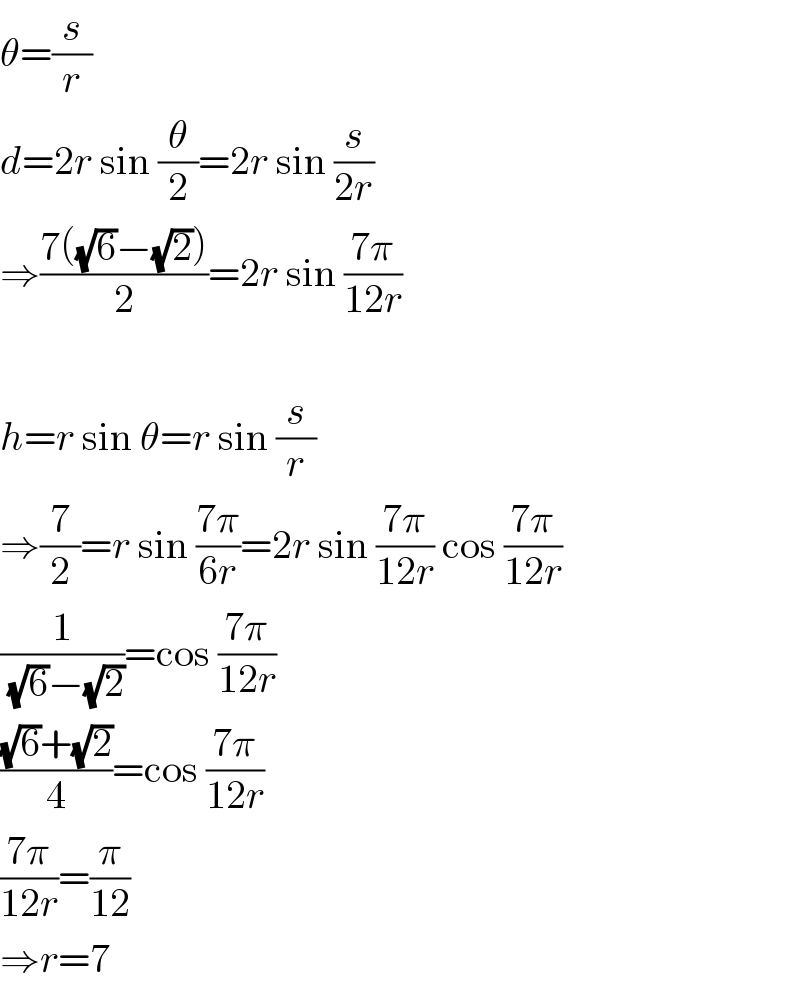
$$\theta=\frac{{s}}{{r}} \\ $$$${d}=\mathrm{2}{r}\:\mathrm{sin}\:\frac{\theta}{\mathrm{2}}=\mathrm{2}{r}\:\mathrm{sin}\:\frac{{s}}{\mathrm{2}{r}} \\ $$$$\Rightarrow\frac{\mathrm{7}\left(\sqrt{\mathrm{6}}−\sqrt{\mathrm{2}}\right)}{\mathrm{2}}=\mathrm{2}{r}\:\mathrm{sin}\:\frac{\mathrm{7}\pi}{\mathrm{12}{r}} \\ $$$$ \\ $$$${h}={r}\:\mathrm{sin}\:\theta={r}\:\mathrm{sin}\:\frac{{s}}{{r}} \\ $$$$\Rightarrow\frac{\mathrm{7}}{\mathrm{2}}={r}\:\mathrm{sin}\:\frac{\mathrm{7}\pi}{\mathrm{6}{r}}=\mathrm{2}{r}\:\mathrm{sin}\:\frac{\mathrm{7}\pi}{\mathrm{12}{r}}\:\mathrm{cos}\:\frac{\mathrm{7}\pi}{\mathrm{12}{r}} \\ $$$$\frac{\mathrm{1}}{\:\sqrt{\mathrm{6}}−\sqrt{\mathrm{2}}}=\mathrm{cos}\:\frac{\mathrm{7}\pi}{\mathrm{12}{r}} \\ $$$$\frac{\sqrt{\mathrm{6}}+\sqrt{\mathrm{2}}}{\mathrm{4}}=\mathrm{cos}\:\frac{\mathrm{7}\pi}{\mathrm{12}{r}} \\ $$$$\frac{\mathrm{7}\pi}{\mathrm{12}{r}}=\frac{\pi}{\mathrm{12}} \\ $$$$\Rightarrow{r}=\mathrm{7} \\ $$
