Question Number 82232 by mhmd last updated on 19/Feb/20

Commented by JDamian last updated on 19/Feb/20
$$\mathrm{I}\:\mathrm{guess}\:\mathrm{eventually}\:\mathrm{we}\:\mathrm{will}\:\mathrm{have}\:\mathrm{to}\:\mathrm{bear}\:\mathrm{ads} \\ $$
Answered by mind is power last updated on 19/Feb/20
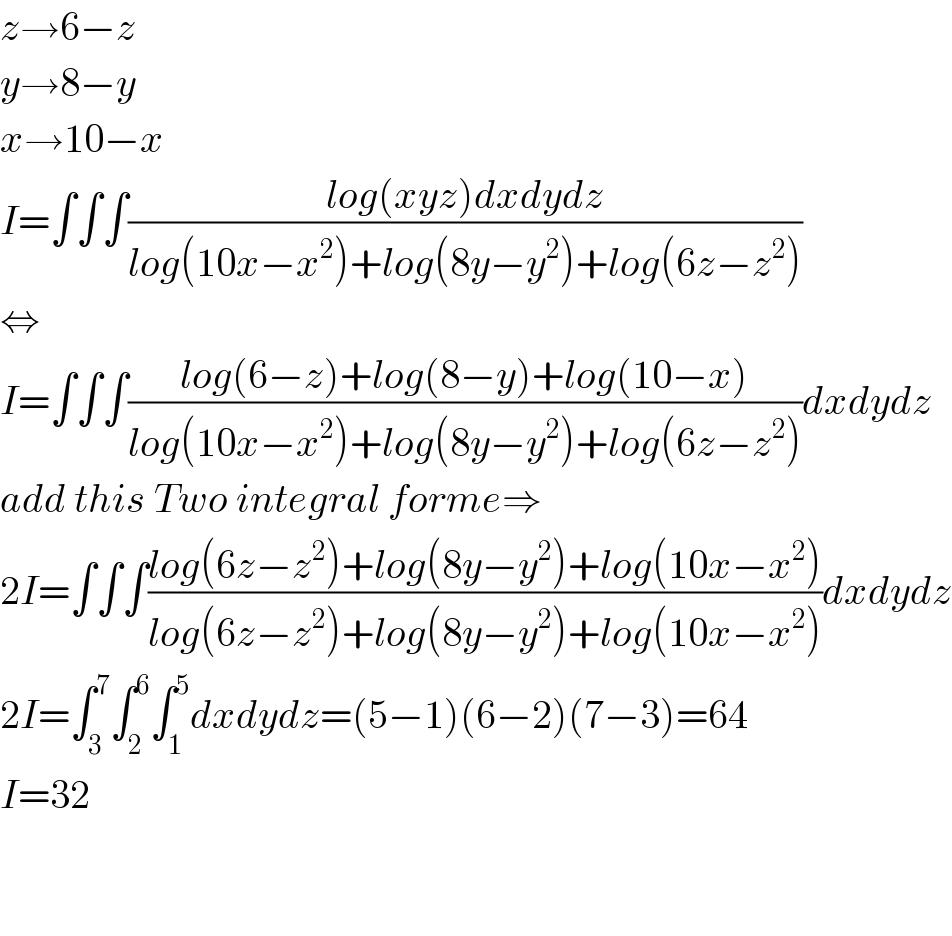
$${z}\rightarrow\mathrm{6}−{z} \\ $$$${y}\rightarrow\mathrm{8}−{y} \\ $$$${x}\rightarrow\mathrm{10}−{x} \\ $$$${I}=\int\int\int\frac{{log}\left({xyz}\right){dxdydz}}{{log}\left(\mathrm{10}{x}−{x}^{\mathrm{2}} \right)+{log}\left(\mathrm{8}{y}−{y}^{\mathrm{2}} \right)+{log}\left(\mathrm{6}{z}−{z}^{\mathrm{2}} \right)} \\ $$$$\Leftrightarrow \\ $$$${I}=\int\int\int\frac{{log}\left(\mathrm{6}−{z}\right)+{log}\left(\mathrm{8}−{y}\right)+{log}\left(\mathrm{10}−{x}\right)}{{log}\left(\mathrm{10}{x}−{x}^{\mathrm{2}} \right)+{log}\left(\mathrm{8}{y}−{y}^{\mathrm{2}} \right)+{log}\left(\mathrm{6}{z}−{z}^{\mathrm{2}} \right)}{dxdydz} \\ $$$${add}\:{this}\:{Two}\:{integral}\:{forme}\Rightarrow \\ $$$$\mathrm{2}{I}=\int\int\int\frac{{log}\left(\mathrm{6}{z}−{z}^{\mathrm{2}} \right)+{log}\left(\mathrm{8}{y}−{y}^{\mathrm{2}} \right)+{log}\left(\mathrm{10}{x}−{x}^{\mathrm{2}} \right)}{{log}\left(\mathrm{6}{z}−{z}^{\mathrm{2}} \right)+{log}\left(\mathrm{8}{y}−{y}^{\mathrm{2}} \right)+{log}\left(\mathrm{10}{x}−{x}^{\mathrm{2}} \right)}{dxdydz} \\ $$$$\mathrm{2}{I}=\int_{\mathrm{3}} ^{\mathrm{7}} \int_{\mathrm{2}} ^{\mathrm{6}} \int_{\mathrm{1}} ^{\mathrm{5}} {dxdydz}=\left(\mathrm{5}−\mathrm{1}\right)\left(\mathrm{6}−\mathrm{2}\right)\left(\mathrm{7}−\mathrm{3}\right)=\mathrm{64} \\ $$$${I}=\mathrm{32} \\ $$$$ \\ $$$$ \\ $$
Commented by mhmd last updated on 19/Feb/20

$${thank}\:{you}\:{sir} \\ $$
Commented by mind is power last updated on 19/Feb/20

$${withe}\:{pleasur} \\ $$
