Question Number 82243 by M±th+et£s last updated on 19/Feb/20

Answered by mind is power last updated on 19/Feb/20
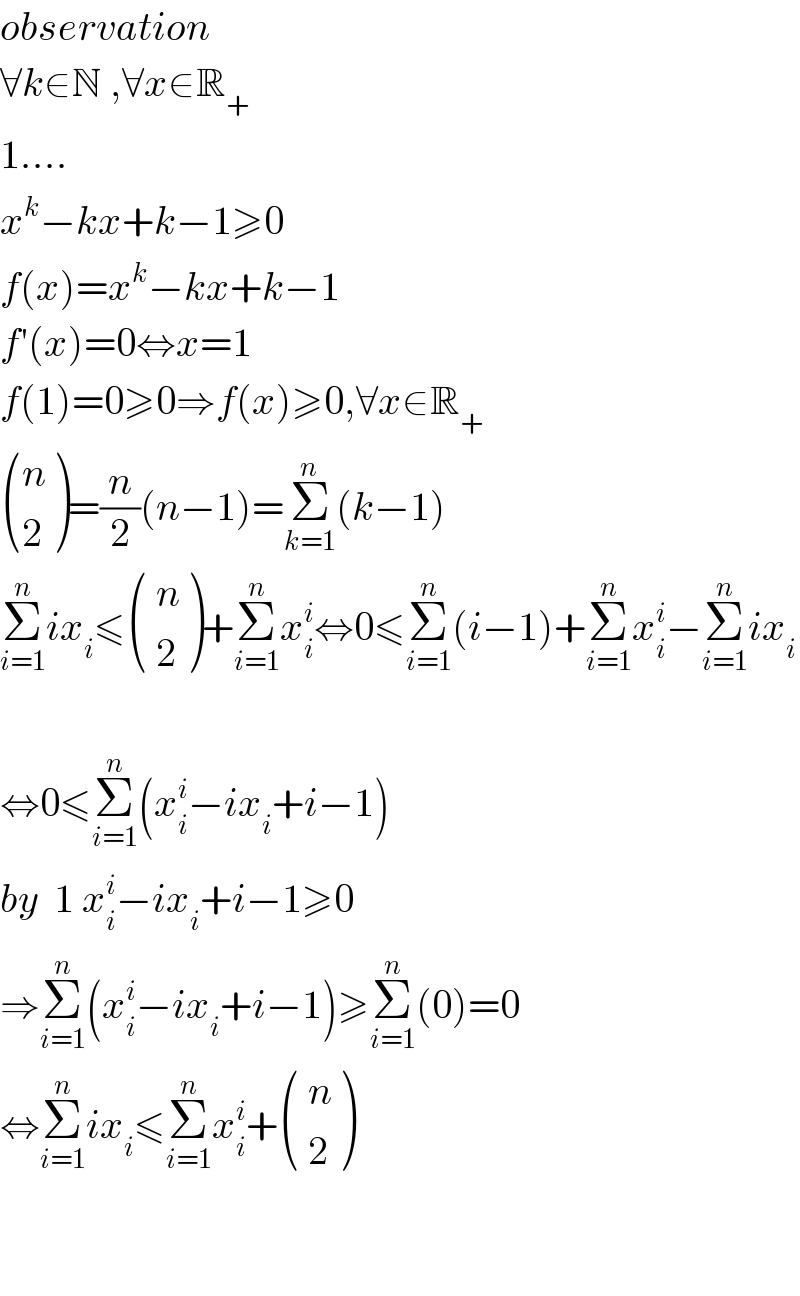
$${observation} \\ $$$$\forall{k}\in\mathbb{N}\:,\forall{x}\in\mathbb{R}_{+} \\ $$$$\mathrm{1}…. \\ $$$${x}^{{k}} −{kx}+{k}−\mathrm{1}\geqslant\mathrm{0} \\ $$$${f}\left({x}\right)={x}^{{k}} −{kx}+{k}−\mathrm{1} \\ $$$${f}'\left({x}\right)=\mathrm{0}\Leftrightarrow{x}=\mathrm{1} \\ $$$${f}\left(\mathrm{1}\right)=\mathrm{0}\geqslant\mathrm{0}\Rightarrow{f}\left({x}\right)\geqslant\mathrm{0},\forall{x}\in\mathbb{R}_{+} \\ $$$$\begin{pmatrix}{{n}}\\{\mathrm{2}}\end{pmatrix}=\frac{{n}}{\mathrm{2}}\left({n}−\mathrm{1}\right)=\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\left({k}−\mathrm{1}\right) \\ $$$$\underset{{i}=\mathrm{1}} {\overset{{n}} {\sum}}{ix}_{{i}} \leqslant\begin{pmatrix}{\:{n}}\\{\:\mathrm{2}}\end{pmatrix}+\underset{{i}=\mathrm{1}} {\overset{{n}} {\sum}}{x}_{{i}} ^{{i}} \Leftrightarrow\mathrm{0}\leqslant\underset{{i}=\mathrm{1}} {\overset{{n}} {\sum}}\left({i}−\mathrm{1}\right)+\underset{{i}=\mathrm{1}} {\overset{{n}} {\sum}}{x}_{{i}} ^{{i}} −\underset{{i}=\mathrm{1}} {\overset{{n}} {\sum}}{ix}_{{i}} \\ $$$$ \\ $$$$\Leftrightarrow\mathrm{0}\leqslant\underset{{i}=\mathrm{1}} {\overset{{n}} {\sum}}\left({x}_{{i}} ^{{i}} −{ix}_{{i}} +{i}−\mathrm{1}\right) \\ $$$${by}\:\:\mathrm{1}\:{x}_{{i}} ^{{i}} −{ix}_{{i}} +{i}−\mathrm{1}\geqslant\mathrm{0} \\ $$$$\Rightarrow\underset{{i}=\mathrm{1}} {\overset{{n}} {\sum}}\left({x}_{{i}} ^{{i}} −{ix}_{{i}} +{i}−\mathrm{1}\right)\geqslant\underset{{i}=\mathrm{1}} {\overset{{n}} {\sum}}\left(\mathrm{0}\right)=\mathrm{0}\: \\ $$$$\Leftrightarrow\underset{{i}=\mathrm{1}} {\overset{{n}} {\sum}}{ix}_{{i}} \leqslant\underset{{i}=\mathrm{1}} {\overset{{n}} {\sum}}{x}_{{i}} ^{{i}} +\begin{pmatrix}{\:{n}}\\{\:\mathrm{2}}\end{pmatrix} \\ $$$$ \\ $$$$ \\ $$
Commented by M±th+et£s last updated on 19/Feb/20
$${nice}\:{solution}\:{sir}\:{thank}\:{you} \\ $$
Commented by mind is power last updated on 20/Feb/20

$${withe}\:{pleasur} \\ $$
