Question Number 82307 by Power last updated on 20/Feb/20
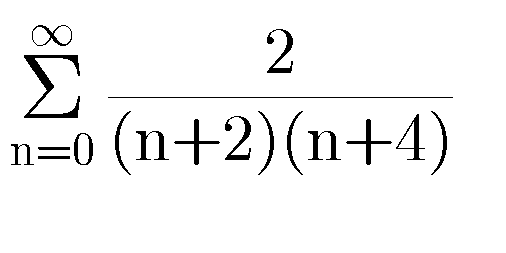
Commented by Tony Lin last updated on 20/Feb/20

$$\underset{{n}=\mathrm{3}} {\overset{\infty} {\sum}}\frac{\mathrm{2}}{\left({n}−\mathrm{1}\right)\left({n}+\mathrm{1}\right)} \\ $$$$=\underset{{n}=\mathrm{3}} {\overset{\infty} {\sum}}\left(\frac{\mathrm{1}}{{n}−\mathrm{1}}−\frac{\mathrm{1}}{{n}+\mathrm{1}}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{3}}−\frac{\mathrm{1}}{\mathrm{5}}+\frac{\mathrm{1}}{\mathrm{4}}−\frac{\mathrm{1}}{\mathrm{6}}+\frac{\mathrm{1}}{\mathrm{5}}−\frac{\mathrm{1}}{\mathrm{7}}+\centerdot\centerdot\centerdot \\ $$$$=\frac{\mathrm{5}}{\mathrm{6}} \\ $$
Commented by Power last updated on 20/Feb/20

$$\mathrm{thanks} \\ $$
Commented by mathmax by abdo last updated on 20/Feb/20

$${let}\:{S}_{{n}} =\sum_{{k}=\mathrm{0}} ^{{n}} \:\frac{\mathrm{2}}{\left({k}+\mathrm{2}\right)\left({k}+\mathrm{4}\right)}\:\Rightarrow{S}_{{n}} =\sum_{{k}=\mathrm{0}} ^{{n}} \left(\frac{\mathrm{1}}{{k}+\mathrm{2}}−\frac{\mathrm{1}}{{k}+\mathrm{4}}\right) \\ $$$$=\sum_{{k}=\mathrm{0}} ^{{n}} \:\frac{\mathrm{1}}{{k}+\mathrm{2}}\:−\sum_{{k}=\mathrm{0}} ^{{n}} \:\frac{\mathrm{1}}{{k}+\mathrm{4}}\:\:{but} \\ $$$$\sum_{{k}=\mathrm{0}} ^{{n}} \:\frac{\mathrm{1}}{{k}+\mathrm{2}}=\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{3}}\:+\sum_{{k}=\mathrm{2}} ^{{n}} \:\frac{\mathrm{1}}{{k}+\mathrm{2}}\:=\frac{\mathrm{5}}{\mathrm{6}}+\:\sum_{{p}=\mathrm{0}} ^{{n}−\mathrm{2}} \:\frac{\mathrm{1}}{{p}+\mathrm{4}}\:\:\:\:\:\:\left({k}={p}+\mathrm{2}\right) \\ $$$$\Rightarrow\:{S}_{{n}} =\frac{\mathrm{5}}{\mathrm{6}}\:+\sum_{{p}=\mathrm{0}} ^{{n}−\mathrm{2}} \:\frac{\mathrm{1}}{{p}+\mathrm{4}}−\sum_{{p}=\mathrm{0}} ^{{n}} \:\frac{\mathrm{1}}{{p}+\mathrm{4}} \\ $$$$=\frac{\mathrm{5}}{\mathrm{6}}−\frac{\mathrm{1}}{{n}+\mathrm{3}}−\frac{\mathrm{1}}{{n}+\mathrm{4}}\:\Rightarrow{lim}_{{n}\rightarrow+\infty} \:{S}_{{n}} =\frac{\mathrm{5}}{\mathrm{6}} \\ $$
