Question Number 82378 by ajfour last updated on 20/Feb/20
Commented by ajfour last updated on 20/Feb/20
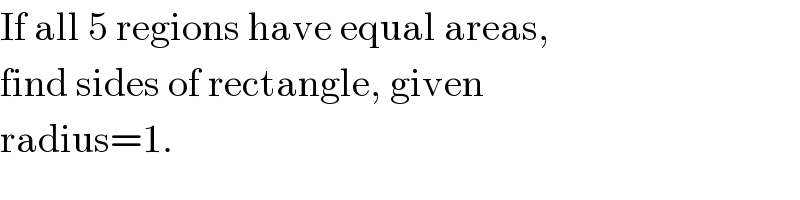
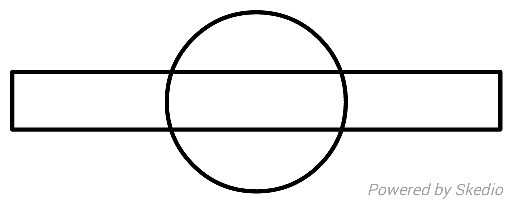
$$\mathrm{If}\:\mathrm{all}\:\mathrm{5}\:\mathrm{regions}\:\mathrm{have}\:\mathrm{equal}\:\mathrm{areas}, \\ $$$$\mathrm{find}\:\mathrm{sides}\:\mathrm{of}\:\mathrm{rectangle},\:\mathrm{given} \\ $$$$\mathrm{radius}=\mathrm{1}. \\ $$
Answered by mr W last updated on 21/Feb/20
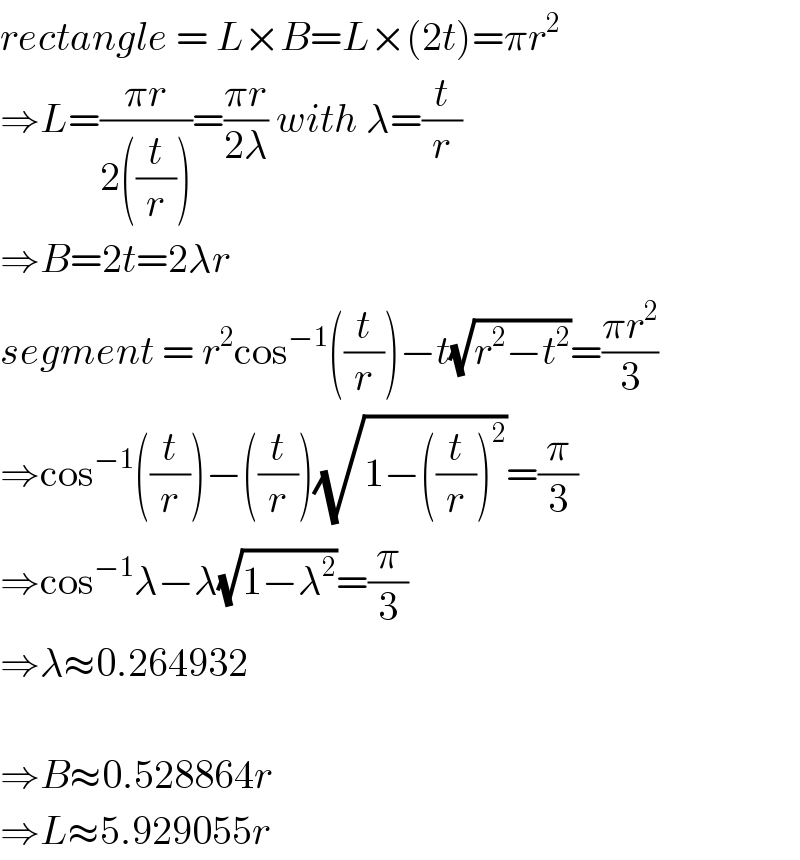
$${rectangle}\:=\:{L}×{B}={L}×\left(\mathrm{2}{t}\right)=\pi{r}^{\mathrm{2}} \\ $$$$\Rightarrow{L}=\frac{\pi{r}}{\mathrm{2}\left(\frac{{t}}{{r}}\right)}=\frac{\pi{r}}{\mathrm{2}\lambda}\:{with}\:\lambda=\frac{{t}}{{r}} \\ $$$$\Rightarrow{B}=\mathrm{2}{t}=\mathrm{2}\lambda{r} \\ $$$${segment}\:=\:{r}^{\mathrm{2}} \mathrm{cos}^{−\mathrm{1}} \left(\frac{{t}}{{r}}\right)−{t}\sqrt{{r}^{\mathrm{2}} −{t}^{\mathrm{2}} }=\frac{\pi{r}^{\mathrm{2}} }{\mathrm{3}} \\ $$$$\Rightarrow\mathrm{cos}^{−\mathrm{1}} \left(\frac{{t}}{{r}}\right)−\left(\frac{{t}}{{r}}\right)\sqrt{\mathrm{1}−\left(\frac{{t}}{{r}}\right)^{\mathrm{2}} }=\frac{\pi}{\mathrm{3}} \\ $$$$\Rightarrow\mathrm{cos}^{−\mathrm{1}} \lambda−\lambda\sqrt{\mathrm{1}−\lambda^{\mathrm{2}} }=\frac{\pi}{\mathrm{3}} \\ $$$$\Rightarrow\lambda\approx\mathrm{0}.\mathrm{264932} \\ $$$$ \\ $$$$\Rightarrow{B}\approx\mathrm{0}.\mathrm{528864}{r} \\ $$$$\Rightarrow{L}\approx\mathrm{5}.\mathrm{929055}{r} \\ $$
Commented by ajfour last updated on 22/Feb/20
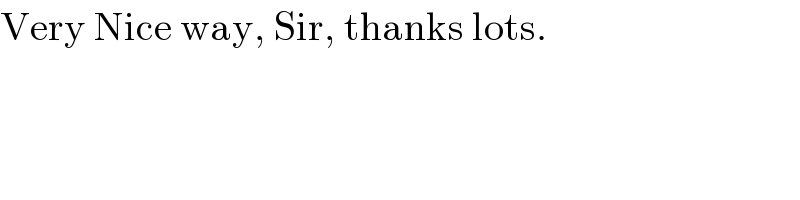
$$\mathrm{Very}\:\mathrm{Nice}\:\mathrm{way},\:\mathrm{Sir},\:\mathrm{thanks}\:\mathrm{lots}. \\ $$
