Question Number 82404 by jagoll last updated on 21/Feb/20

Commented by jagoll last updated on 21/Feb/20
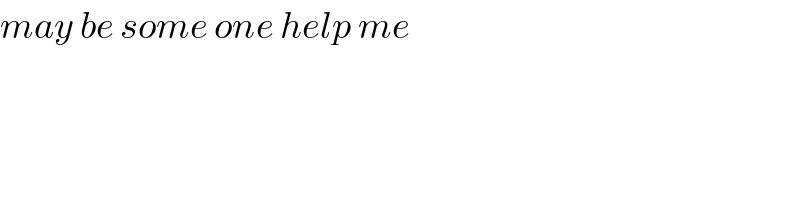
$${may}\:{be}\:{some}\:{one}\:{help}\:{me} \\ $$
Commented by mr W last updated on 21/Feb/20
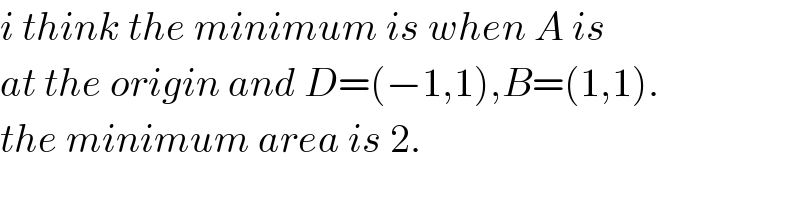
$${i}\:{think}\:{the}\:{minimum}\:{is}\:{when}\:{A}\:{is} \\ $$$${at}\:{the}\:{origin}\:{and}\:{D}=\left(−\mathrm{1},\mathrm{1}\right),{B}=\left(\mathrm{1},\mathrm{1}\right). \\ $$$${the}\:{minimum}\:{area}\:{is}\:\mathrm{2}. \\ $$
Commented by jagoll last updated on 21/Feb/20

$${point}\:{C}\:{sir}\:? \\ $$
Commented by jagoll last updated on 21/Feb/20

$${does}\:{mean}\:{the}\:{point}\:{C}\:{must} \\ $$$${lie}\:{on}\:{y}−{axis} \\ $$
Commented by mr W last updated on 21/Feb/20

$${my}\:{understanding}\:{is}\:{that}\:{three}\:{vertices}\: \\ $$$${should}\:{lie}\:{on}\:{the}\:{parabola}\:{and}\:{the}\: \\ $$$${fourth}\:{vextex}\:{not}.\:{whether}\:{the}\:{fourth} \\ $$$${vertex}\:{is}\:{outside}\:{or}\:{inside}\:{of}\:{the} \\ $$$${parabola},\:{it}\:{doesn}'{t}\:{matter}.\:{but}\:{this} \\ $$$${is}\:{your}\:{question}.\:{what}\:{do}\:{you}\:{mean}? \\ $$$${should}\:{the}\:{fourth}\:{vertex}\:{only}\:{outside} \\ $$$${of}\:{the}\:{parabola}\:{or}\:{it}\:{doesn}'{t}\:{matter}? \\ $$
Commented by jagoll last updated on 21/Feb/20

$${if}\:{according}\:{to}\:{my}\:{understanding} \\ $$$${the}\:{fourth}\:{point}\:{is}\:{outside}\:{parabola}. \\ $$$${dish}\:{according}\:{to}\:{the}\:{picture} \\ $$$${shown}\:{in}\:{the}\:{problem}.\:{sir} \\ $$
Commented by mr W last updated on 21/Feb/20

$${solution}\:{for}\:{the}\:{case}\:{that}\:{the}\:{fourth} \\ $$$${vertex}\:{lies}\:{outside}\:{the}\:{parabola} \\ $$$${see}\:{below}. \\ $$
Answered by mr W last updated on 21/Feb/20
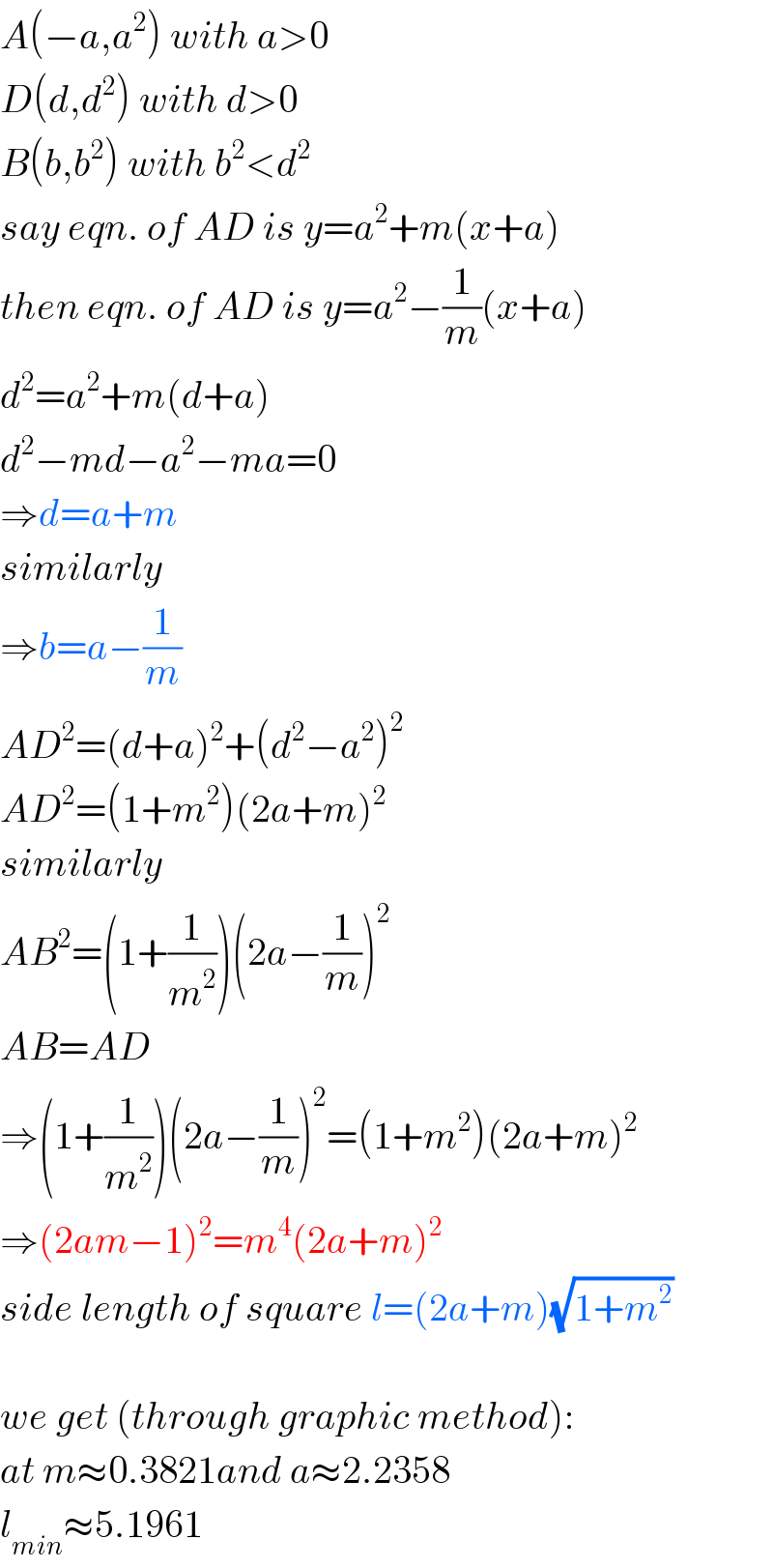
$${A}\left(−{a},{a}^{\mathrm{2}} \right)\:{with}\:{a}>\mathrm{0} \\ $$$${D}\left({d},{d}^{\mathrm{2}} \right)\:{with}\:{d}>\mathrm{0} \\ $$$${B}\left({b},{b}^{\mathrm{2}} \right)\:{with}\:{b}^{\mathrm{2}} <{d}^{\mathrm{2}} \\ $$$${say}\:{eqn}.\:{of}\:{AD}\:{is}\:{y}={a}^{\mathrm{2}} +{m}\left({x}+{a}\right) \\ $$$${then}\:{eqn}.\:{of}\:{AD}\:{is}\:{y}={a}^{\mathrm{2}} −\frac{\mathrm{1}}{{m}}\left({x}+{a}\right) \\ $$$${d}^{\mathrm{2}} ={a}^{\mathrm{2}} +{m}\left({d}+{a}\right) \\ $$$${d}^{\mathrm{2}} −{md}−{a}^{\mathrm{2}} −{ma}=\mathrm{0} \\ $$$$\Rightarrow{d}={a}+{m} \\ $$$${similarly} \\ $$$$\Rightarrow{b}={a}−\frac{\mathrm{1}}{{m}} \\ $$$${AD}^{\mathrm{2}} =\left({d}+{a}\right)^{\mathrm{2}} +\left({d}^{\mathrm{2}} −{a}^{\mathrm{2}} \right)^{\mathrm{2}} \\ $$$${AD}^{\mathrm{2}} =\left(\mathrm{1}+{m}^{\mathrm{2}} \right)\left(\mathrm{2}{a}+{m}\right)^{\mathrm{2}} \\ $$$${similarly} \\ $$$${AB}^{\mathrm{2}} =\left(\mathrm{1}+\frac{\mathrm{1}}{{m}^{\mathrm{2}} }\right)\left(\mathrm{2}{a}−\frac{\mathrm{1}}{{m}}\right)^{\mathrm{2}} \\ $$$${AB}={AD} \\ $$$$\Rightarrow\left(\mathrm{1}+\frac{\mathrm{1}}{{m}^{\mathrm{2}} }\right)\left(\mathrm{2}{a}−\frac{\mathrm{1}}{{m}}\right)^{\mathrm{2}} =\left(\mathrm{1}+{m}^{\mathrm{2}} \right)\left(\mathrm{2}{a}+{m}\right)^{\mathrm{2}} \\ $$$$\Rightarrow\left(\mathrm{2}{am}−\mathrm{1}\right)^{\mathrm{2}} ={m}^{\mathrm{4}} \left(\mathrm{2}{a}+{m}\right)^{\mathrm{2}} \\ $$$${side}\:{length}\:{of}\:{square}\:{l}=\left(\mathrm{2}{a}+{m}\right)\sqrt{\mathrm{1}+{m}^{\mathrm{2}} } \\ $$$$ \\ $$$${we}\:{get}\:\left({through}\:{graphic}\:{method}\right): \\ $$$${at}\:{m}\approx\mathrm{0}.\mathrm{3821}{and}\:{a}\approx\mathrm{2}.\mathrm{2358} \\ $$$${l}_{{min}} \approx\mathrm{5}.\mathrm{1961} \\ $$
Commented by mr W last updated on 21/Feb/20

Commented by mr W last updated on 21/Feb/20

Commented by mr W last updated on 21/Feb/20
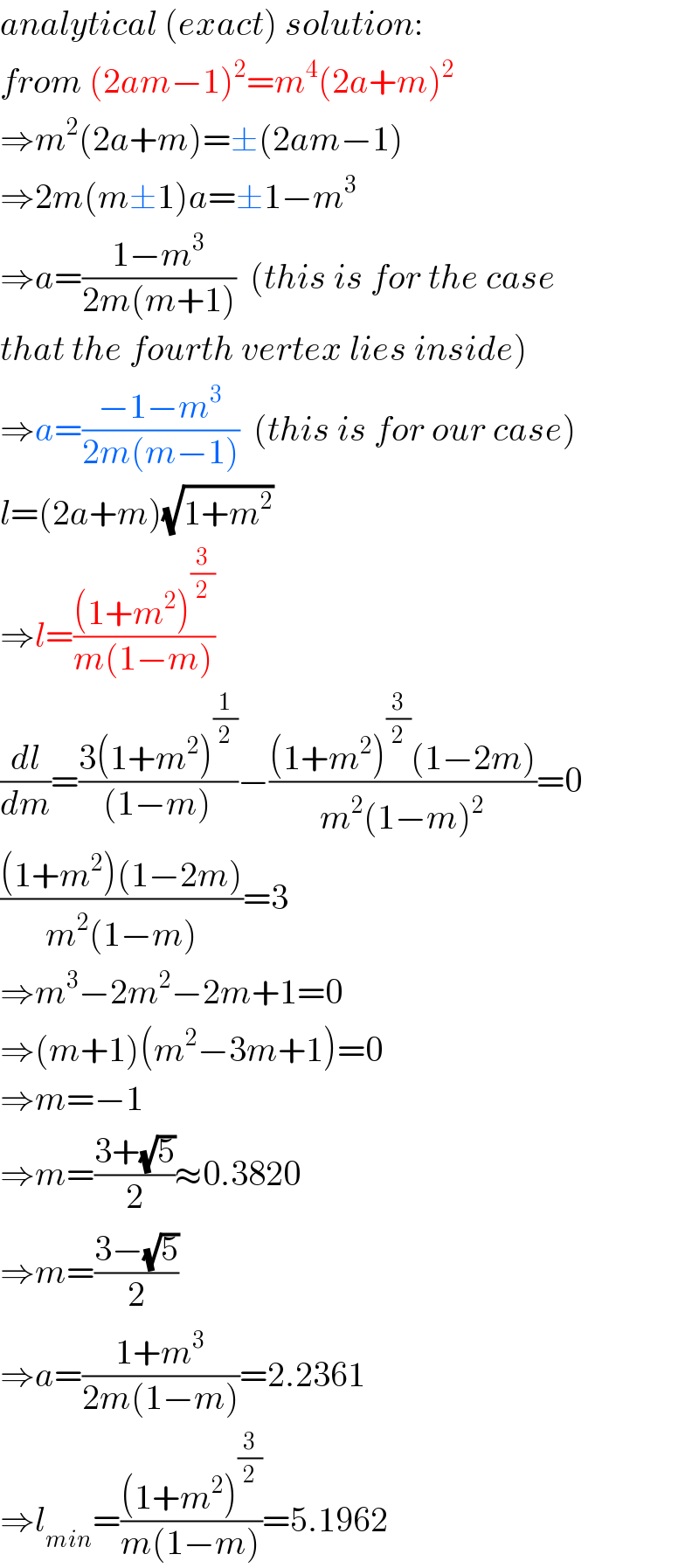
$${analytical}\:\left({exact}\right)\:{solution}: \\ $$$${from}\:\left(\mathrm{2}{am}−\mathrm{1}\right)^{\mathrm{2}} ={m}^{\mathrm{4}} \left(\mathrm{2}{a}+{m}\right)^{\mathrm{2}} \\ $$$$\Rightarrow{m}^{\mathrm{2}} \left(\mathrm{2}{a}+{m}\right)=\pm\left(\mathrm{2}{am}−\mathrm{1}\right) \\ $$$$\Rightarrow\mathrm{2}{m}\left({m}\pm\mathrm{1}\right){a}=\pm\mathrm{1}−{m}^{\mathrm{3}} \\ $$$$\Rightarrow{a}=\frac{\mathrm{1}−{m}^{\mathrm{3}} }{\mathrm{2}{m}\left({m}+\mathrm{1}\right)}\:\:\left({this}\:{is}\:{for}\:{the}\:{case}\right. \\ $$$$\left.{that}\:{the}\:{fourth}\:{vertex}\:{lies}\:{inside}\right) \\ $$$$\Rightarrow{a}=\frac{−\mathrm{1}−{m}^{\mathrm{3}} }{\mathrm{2}{m}\left({m}−\mathrm{1}\right)}\:\:\left({this}\:{is}\:{for}\:{our}\:{case}\right) \\ $$$${l}=\left(\mathrm{2}{a}+{m}\right)\sqrt{\mathrm{1}+{m}^{\mathrm{2}} } \\ $$$$\Rightarrow{l}=\frac{\left(\mathrm{1}+{m}^{\mathrm{2}} \right)^{\frac{\mathrm{3}}{\mathrm{2}}} }{{m}\left(\mathrm{1}−{m}\right)} \\ $$$$\frac{{dl}}{{dm}}=\frac{\mathrm{3}\left(\mathrm{1}+{m}^{\mathrm{2}} \right)^{\frac{\mathrm{1}}{\mathrm{2}}} }{\left(\mathrm{1}−{m}\right)}−\frac{\left(\mathrm{1}+{m}^{\mathrm{2}} \right)^{\frac{\mathrm{3}}{\mathrm{2}}} \left(\mathrm{1}−\mathrm{2}{m}\right)}{{m}^{\mathrm{2}} \left(\mathrm{1}−{m}\right)^{\mathrm{2}} }=\mathrm{0} \\ $$$$\frac{\left(\mathrm{1}+{m}^{\mathrm{2}} \right)\left(\mathrm{1}−\mathrm{2}{m}\right)}{{m}^{\mathrm{2}} \left(\mathrm{1}−{m}\right)}=\mathrm{3} \\ $$$$\Rightarrow{m}^{\mathrm{3}} −\mathrm{2}{m}^{\mathrm{2}} −\mathrm{2}{m}+\mathrm{1}=\mathrm{0} \\ $$$$\Rightarrow\left({m}+\mathrm{1}\right)\left({m}^{\mathrm{2}} −\mathrm{3}{m}+\mathrm{1}\right)=\mathrm{0} \\ $$$$\Rightarrow{m}=−\mathrm{1} \\ $$$$\Rightarrow{m}=\frac{\mathrm{3}+\sqrt{\mathrm{5}}}{\mathrm{2}}\approx\mathrm{0}.\mathrm{3820} \\ $$$$\Rightarrow{m}=\frac{\mathrm{3}−\sqrt{\mathrm{5}}}{\mathrm{2}} \\ $$$$\Rightarrow{a}=\frac{\mathrm{1}+{m}^{\mathrm{3}} }{\mathrm{2}{m}\left(\mathrm{1}−{m}\right)}=\mathrm{2}.\mathrm{2361} \\ $$$$\Rightarrow{l}_{{min}} =\frac{\left(\mathrm{1}+{m}^{\mathrm{2}} \right)^{\frac{\mathrm{3}}{\mathrm{2}}} }{{m}\left(\mathrm{1}−{m}\right)}=\mathrm{5}.\mathrm{1962} \\ $$
Commented by mr W last updated on 21/Feb/20

Commented by mr W last updated on 21/Feb/20

Commented by mr W last updated on 21/Feb/20

Commented by jagoll last updated on 21/Feb/20

$${yes}\:{sir}\:{thank}\:{you} \\ $$
