Question Number 82410 by naka3546 last updated on 21/Feb/20

Commented by naka3546 last updated on 21/Feb/20
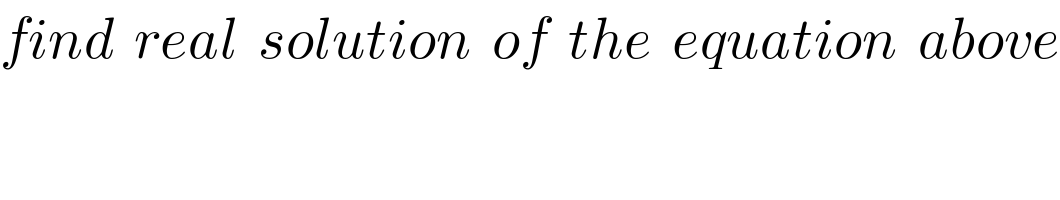
$${find}\:\:{real}\:\:{solution}\:\:{of}\:\:{the}\:\:{equation}\:\:{above} \\ $$
Answered by MJS last updated on 21/Feb/20
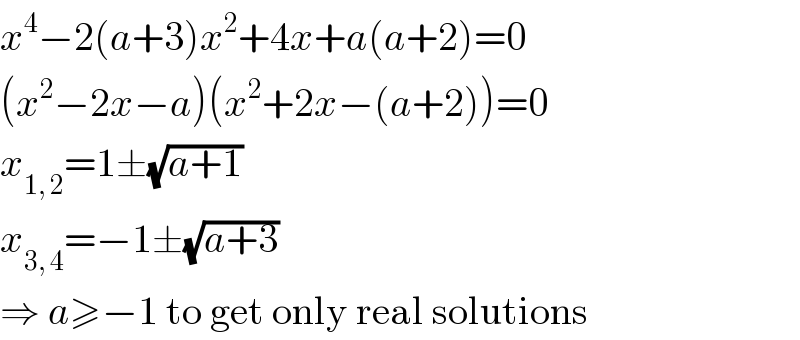
$${x}^{\mathrm{4}} −\mathrm{2}\left({a}+\mathrm{3}\right){x}^{\mathrm{2}} +\mathrm{4}{x}+{a}\left({a}+\mathrm{2}\right)=\mathrm{0} \\ $$$$\left({x}^{\mathrm{2}} −\mathrm{2}{x}−{a}\right)\left({x}^{\mathrm{2}} +\mathrm{2}{x}−\left({a}+\mathrm{2}\right)\right)=\mathrm{0} \\ $$$${x}_{\mathrm{1},\:\mathrm{2}} =\mathrm{1}\pm\sqrt{{a}+\mathrm{1}} \\ $$$${x}_{\mathrm{3},\:\mathrm{4}} =−\mathrm{1}\pm\sqrt{{a}+\mathrm{3}} \\ $$$$\Rightarrow\:{a}\geqslant−\mathrm{1}\:\mathrm{to}\:\mathrm{get}\:\mathrm{only}\:\mathrm{real}\:\mathrm{solutions} \\ $$
