Question Number 82421 by M±th+et£s last updated on 21/Feb/20
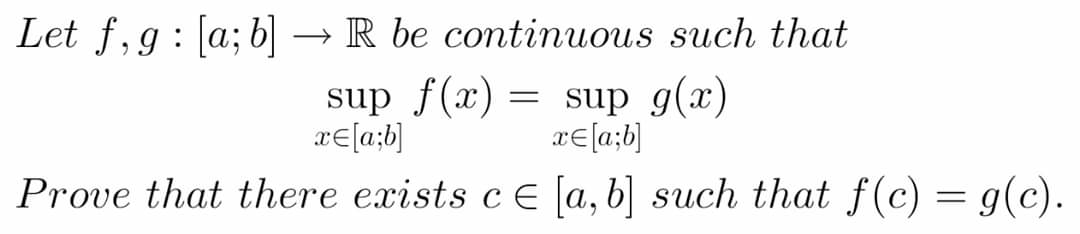
Answered by mind is power last updated on 21/Feb/20
![let y∈[a,b] such sup f=f(y) let z∈[a,b] such sup g=g(z) if z=y⇒c=y⇒f(c)=g(c) if z#y assum z<y let h(x)=f(x)−g(x) h(z)=f(z)−g(z)=supf −g(z)=sup g−g(z)≥0 h(y)=f(y)−sup g=f(y)−supf≤0 ⇒h(z).h(y)≤0 since h is continus ⇒ ∃c∈[z,y] such that h(c)=f(c)−g(c)=0⇔f(c)=g(c)](https://www.tinkutara.com/question/Q82483.png)
$${let}\:{y}\in\left[{a},{b}\right]\:{such}\:{sup}\:{f}={f}\left({y}\right) \\ $$$${let}\:{z}\in\left[{a},{b}\right]\:{such}\:{sup}\:{g}={g}\left({z}\right) \\ $$$${if}\:{z}={y}\Rightarrow{c}={y}\Rightarrow{f}\left({c}\right)={g}\left({c}\right) \\ $$$${if}\:{z}#{y}\:{assum}\:{z}<{y} \\ $$$${let}\:{h}\left({x}\right)={f}\left({x}\right)−{g}\left({x}\right) \\ $$$${h}\left({z}\right)={f}\left({z}\right)−{g}\left({z}\right)={supf}\:−{g}\left({z}\right)={sup}\:{g}−{g}\left({z}\right)\geqslant\mathrm{0} \\ $$$${h}\left({y}\right)={f}\left({y}\right)−{sup}\:{g}={f}\left({y}\right)−{supf}\leqslant\mathrm{0} \\ $$$$\Rightarrow{h}\left({z}\right).{h}\left({y}\right)\leqslant\mathrm{0} \\ $$$${since}\:\:{h}\:{is}\:{continus}\:\Rightarrow\:\exists{c}\in\left[{z},{y}\right]\:{such}\:{that} \\ $$$${h}\left({c}\right)={f}\left({c}\right)−{g}\left({c}\right)=\mathrm{0}\Leftrightarrow{f}\left({c}\right)={g}\left({c}\right) \\ $$
