Question Number 82456 by liki last updated on 21/Feb/20

Commented by abdomathmax last updated on 21/Feb/20
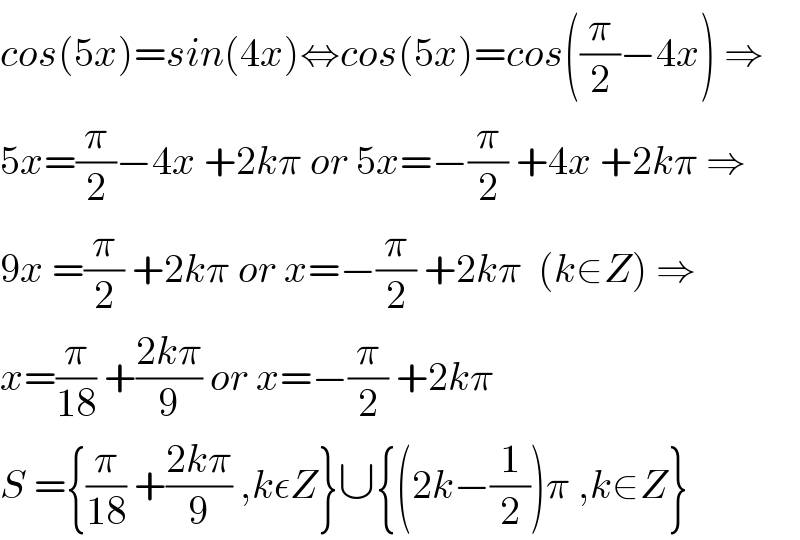
$${cos}\left(\mathrm{5}{x}\right)={sin}\left(\mathrm{4}{x}\right)\Leftrightarrow{cos}\left(\mathrm{5}{x}\right)={cos}\left(\frac{\pi}{\mathrm{2}}−\mathrm{4}{x}\right)\:\Rightarrow \\ $$$$\mathrm{5}{x}=\frac{\pi}{\mathrm{2}}−\mathrm{4}{x}\:+\mathrm{2}{k}\pi\:{or}\:\mathrm{5}{x}=−\frac{\pi}{\mathrm{2}}\:+\mathrm{4}{x}\:+\mathrm{2}{k}\pi\:\Rightarrow \\ $$$$\mathrm{9}{x}\:=\frac{\pi}{\mathrm{2}}\:+\mathrm{2}{k}\pi\:{or}\:{x}=−\frac{\pi}{\mathrm{2}}\:+\mathrm{2}{k}\pi\:\:\left({k}\in{Z}\right)\:\Rightarrow \\ $$$${x}=\frac{\pi}{\mathrm{18}}\:+\frac{\mathrm{2}{k}\pi}{\mathrm{9}}\:{or}\:{x}=−\frac{\pi}{\mathrm{2}}\:+\mathrm{2}{k}\pi \\ $$$${S}\:=\left\{\frac{\pi}{\mathrm{18}}\:+\frac{\mathrm{2}{k}\pi}{\mathrm{9}}\:,{k}\epsilon{Z}\right\}\cup\left\{\left(\mathrm{2}{k}−\frac{\mathrm{1}}{\mathrm{2}}\right)\pi\:,{k}\in{Z}\right\} \\ $$
Commented by jagoll last updated on 21/Feb/20
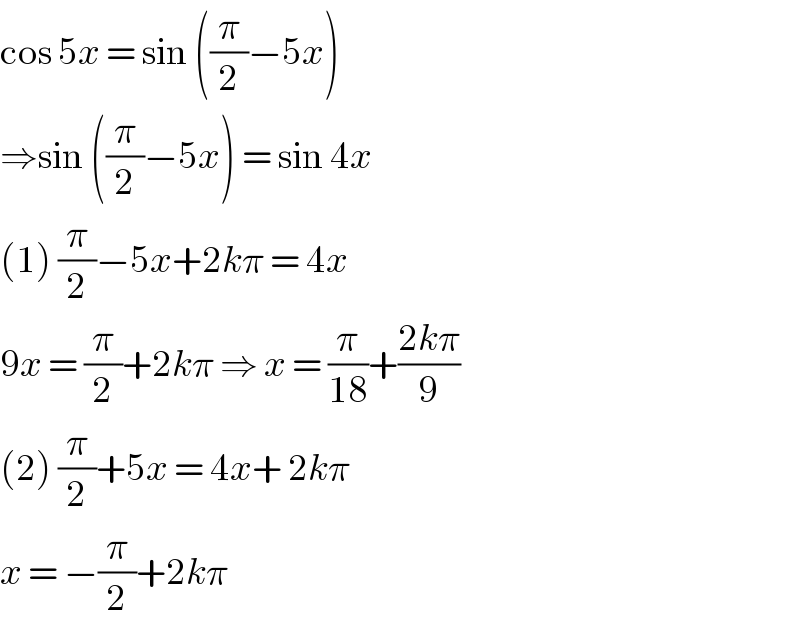
$$\mathrm{cos}\:\mathrm{5}{x}\:=\:\mathrm{sin}\:\left(\frac{\pi}{\mathrm{2}}−\mathrm{5}{x}\right) \\ $$$$\Rightarrow\mathrm{sin}\:\left(\frac{\pi}{\mathrm{2}}−\mathrm{5}{x}\right)\:=\:\mathrm{sin}\:\mathrm{4}{x} \\ $$$$\left(\mathrm{1}\right)\:\frac{\pi}{\mathrm{2}}−\mathrm{5}{x}+\mathrm{2}{k}\pi\:=\:\mathrm{4}{x} \\ $$$$\mathrm{9}{x}\:=\:\frac{\pi}{\mathrm{2}}+\mathrm{2}{k}\pi\:\Rightarrow\:{x}\:=\:\frac{\pi}{\mathrm{18}}+\frac{\mathrm{2}{k}\pi}{\mathrm{9}} \\ $$$$\left(\mathrm{2}\right)\:\frac{\pi}{\mathrm{2}}+\mathrm{5}{x}\:=\:\mathrm{4}{x}+\:\mathrm{2}{k}\pi\: \\ $$$${x}\:=\:−\frac{\pi}{\mathrm{2}}+\mathrm{2}{k}\pi \\ $$
Commented by liki last updated on 21/Feb/20

$$…{thank}\:{you}\:{sir} \\ $$
Commented by liki last updated on 21/Feb/20
$$…{thank}\:{you}\:{very}\:{much}\:{sir}. \\ $$
Commented by liki last updated on 21/Feb/20
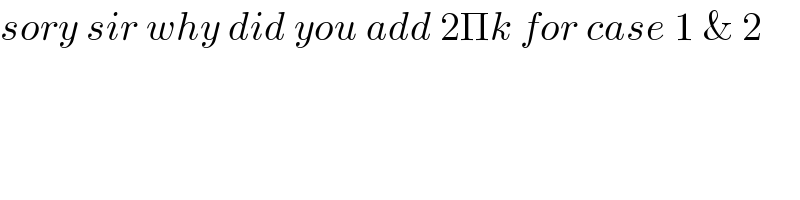
$${sory}\:{sir}\:{why}\:{did}\:{you}\:{add}\:\mathrm{2}\Pi{k}\:{for}\:{case}\:\mathrm{1}\:\&\:\mathrm{2} \\ $$
Commented by abdomathmax last updated on 21/Feb/20
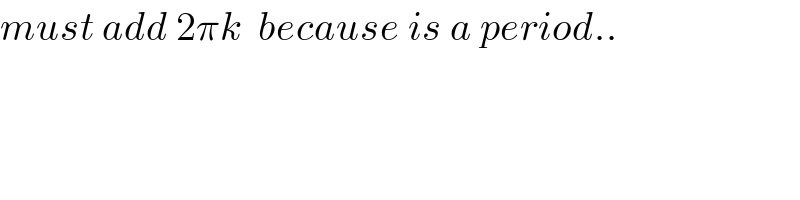
$${must}\:{add}\:\mathrm{2}\pi{k}\:\:{because}\:{is}\:{a}\:{period}.. \\ $$
