Menu Close

Question-82485

Tinku Tara 0 Comments
Pin




Question Number 82485 by naka3546 last updated on 21/Feb/20
Commented by abdomathmax last updated on 21/Feb/20
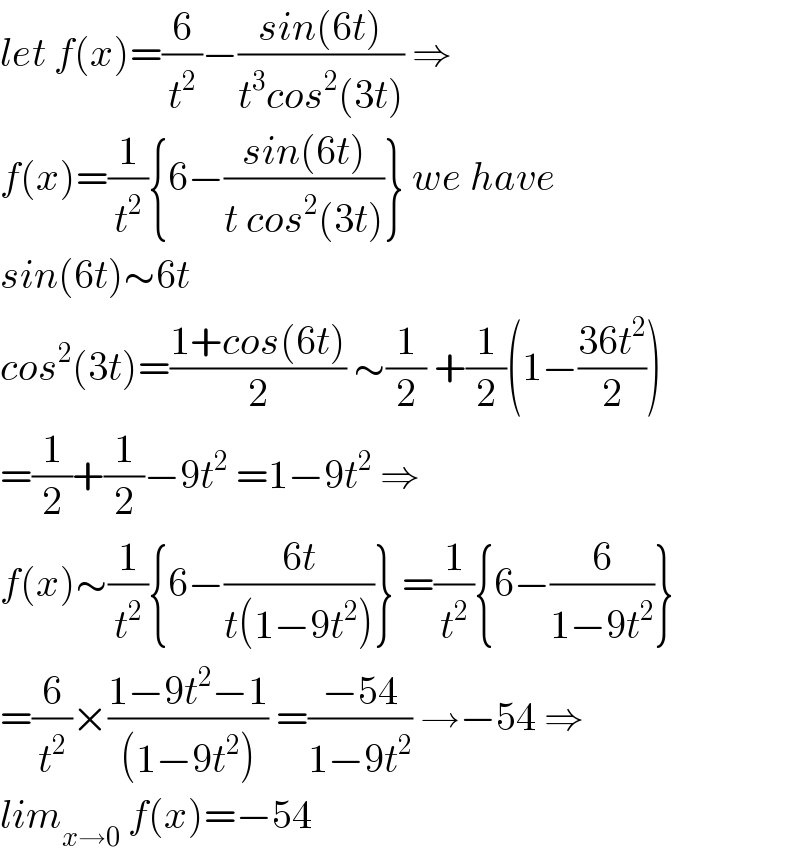
let f(x)=(6/t^2 )−((sin(6t))/(t^3 cos^2 (3t))) ⇒ f(x)=(1/t^2 ){6−((sin(6t))/(t cos^2 (3t)))} we have sin(6t)∼6t cos^2 (3t)=((1+cos(6t))/2) ∼(1/2) +(1/2)(1−((36t^2 )/2)) =(1/2)+(1/2)−9t^2 =1−9t^2 ⇒ f(x)∼(1/t^2 ){6−((6t)/(t(1−9t^2 )))} =(1/t^2 ){6−(6/(1−9t^2 ))} =(6/t^2 )×((1−9t^2 −1)/((1−9t^2 ))) =((−54)/(1−9t^2 )) →−54 ⇒ lim_(x→0) f(x)=−54
$${let}\:{f}\left({x}\right)=\frac{\mathrm{6}}{{t}^{\mathrm{2}} }−\frac{{sin}\left(\mathrm{6}{t}\right)}{{t}^{\mathrm{3}} {cos}^{\mathrm{2}} \left(\mathrm{3}{t}\right)}\:\Rightarrow \\ $$$${f}\left({x}\right)=\frac{\mathrm{1}}{{t}^{\mathrm{2}} }\left\{\mathrm{6}−\frac{{sin}\left(\mathrm{6}{t}\right)}{{t}\:{cos}^{\mathrm{2}} \left(\mathrm{3}{t}\right)}\right\}\:{we}\:{have}\: \\ $$$${sin}\left(\mathrm{6}{t}\right)\sim\mathrm{6}{t} \\ $$$${cos}^{\mathrm{2}} \left(\mathrm{3}{t}\right)=\frac{\mathrm{1}+{cos}\left(\mathrm{6}{t}\right)}{\mathrm{2}}\:\sim\frac{\mathrm{1}}{\mathrm{2}}\:+\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{1}−\frac{\mathrm{36}{t}^{\mathrm{2}} }{\mathrm{2}}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}−\mathrm{9}{t}^{\mathrm{2}} \:=\mathrm{1}−\mathrm{9}{t}^{\mathrm{2}} \:\Rightarrow \\ $$$${f}\left({x}\right)\sim\frac{\mathrm{1}}{{t}^{\mathrm{2}} }\left\{\mathrm{6}−\frac{\mathrm{6}{t}}{{t}\left(\mathrm{1}−\mathrm{9}{t}^{\mathrm{2}} \right)}\right\}\:=\frac{\mathrm{1}}{{t}^{\mathrm{2}} }\left\{\mathrm{6}−\frac{\mathrm{6}}{\mathrm{1}−\mathrm{9}{t}^{\mathrm{2}} }\right\} \\ $$$$=\frac{\mathrm{6}}{{t}^{\mathrm{2}} }×\frac{\mathrm{1}−\mathrm{9}{t}^{\mathrm{2}} −\mathrm{1}}{\left(\mathrm{1}−\mathrm{9}{t}^{\mathrm{2}} \right)}\:=\frac{−\mathrm{54}}{\mathrm{1}−\mathrm{9}{t}^{\mathrm{2}} }\:\rightarrow−\mathrm{54}\:\Rightarrow \\ $$$${lim}_{{x}\rightarrow\mathrm{0}} \:{f}\left({x}\right)=−\mathrm{54} \\ $$
Commented by jagoll last updated on 22/Feb/20
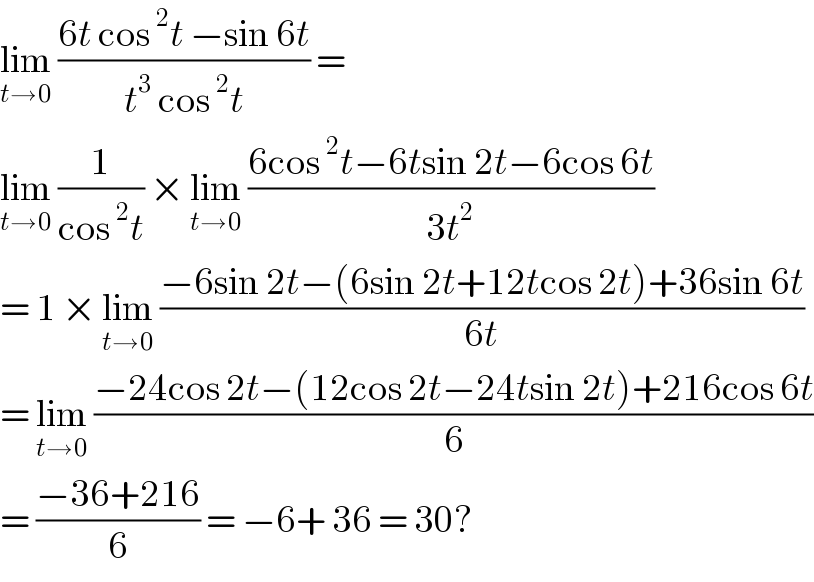
lim_(t→0) ((6t cos^2 t −sin 6t)/(t^3 cos^2 t)) = lim_(t→0) (1/(cos^2 t)) × lim_(t→0) ((6cos^2 t−6tsin 2t−6cos 6t)/(3t^2 )) = 1 × lim_(t→0) ((−6sin 2t−(6sin 2t+12tcos 2t)+36sin 6t)/(6t)) = lim_(t→0) ((−24cos 2t−(12cos 2t−24tsin 2t)+216cos 6t)/6) = ((−36+216)/6) = −6+ 36 = 30?
$$\underset{{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{6}{t}\:\mathrm{cos}\:^{\mathrm{2}} {t}\:−\mathrm{sin}\:\mathrm{6}{t}}{{t}^{\mathrm{3}} \:\mathrm{cos}\:^{\mathrm{2}} {t}}\:=\: \\ $$$$\underset{{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{1}}{\mathrm{cos}\:^{\mathrm{2}} {t}}\:×\:\underset{{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{6cos}\:^{\mathrm{2}} {t}−\mathrm{6}{t}\mathrm{sin}\:\mathrm{2}{t}−\mathrm{6cos}\:\mathrm{6}{t}}{\mathrm{3}{t}^{\mathrm{2}} } \\ $$$$=\:\mathrm{1}\:×\:\underset{{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{−\mathrm{6sin}\:\mathrm{2}{t}−\left(\mathrm{6sin}\:\mathrm{2}{t}+\mathrm{12}{t}\mathrm{cos}\:\mathrm{2}{t}\right)+\mathrm{36sin}\:\mathrm{6}{t}}{\mathrm{6}{t}} \\ $$$$=\:\underset{{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{−\mathrm{24cos}\:\mathrm{2}{t}−\left(\mathrm{12cos}\:\mathrm{2}{t}−\mathrm{24}{t}\mathrm{sin}\:\mathrm{2}{t}\right)+\mathrm{216cos}\:\mathrm{6}{t}}{\mathrm{6}} \\ $$$$=\:\frac{−\mathrm{36}+\mathrm{216}}{\mathrm{6}}\:=\:−\mathrm{6}+\:\mathrm{36}\:=\:\mathrm{30}? \\ $$
Commented by naka3546 last updated on 22/Feb/20
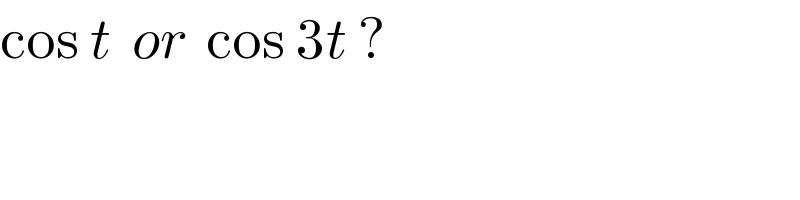
cos t or cos 3t ?
$$\mathrm{cos}\:{t}\:\:{or}\:\:\mathrm{cos}\:\mathrm{3}{t}\:? \\ $$
Commented by john santu last updated on 22/Feb/20
this answer is −18
$${this}\:{answer}\:{is}\:−\mathrm{18} \\ $$
Answered by john santu last updated on 22/Feb/20
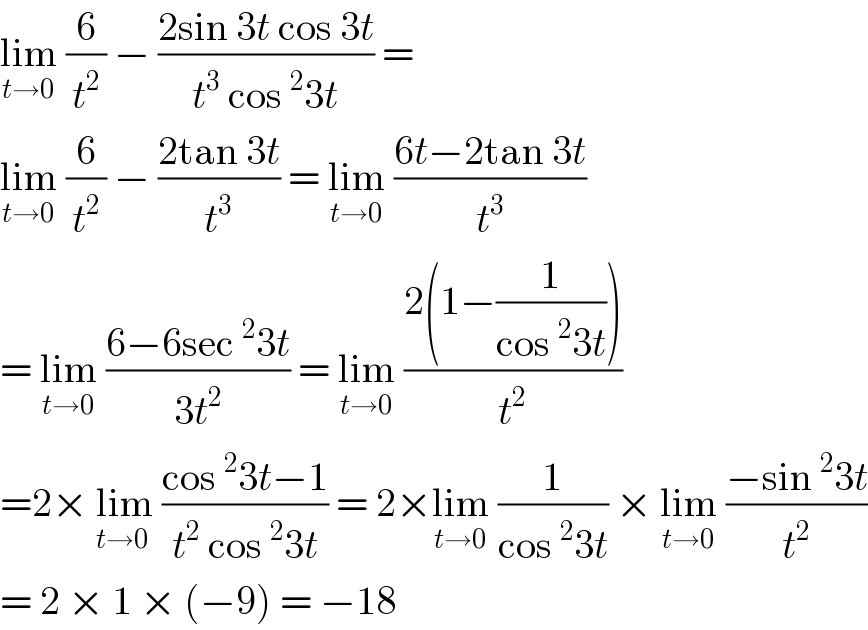
lim_(t→0) (6/t^2 ) − ((2sin 3t cos 3t)/(t^3 cos^2 3t)) = lim_(t→0) (6/t^2 ) − ((2tan 3t)/t^3 ) = lim_(t→0) ((6t−2tan 3t)/t^3 ) = lim_(t→0) ((6−6sec^2 3t)/(3t^2 )) = lim_(t→0) ((2(1−(1/(cos^2 3t))))/t^2 ) =2× lim_(t→0 ) ((cos^2 3t−1)/(t^2 cos^2 3t)) = 2×lim_(t→0) (1/(cos^2 3t)) × lim_(t→0) ((−sin^2 3t)/t^2 ) = 2 × 1 × (−9) = −18
$$\underset{{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{6}}{{t}^{\mathrm{2}} }\:−\:\frac{\mathrm{2sin}\:\mathrm{3}{t}\:\mathrm{cos}\:\mathrm{3}{t}}{{t}^{\mathrm{3}} \:\mathrm{cos}\:^{\mathrm{2}} \mathrm{3}{t}}\:= \\ $$$$\underset{{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{6}}{{t}^{\mathrm{2}} }\:−\:\frac{\mathrm{2tan}\:\mathrm{3}{t}}{{t}^{\mathrm{3}} }\:=\:\underset{{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{6}{t}−\mathrm{2tan}\:\mathrm{3}{t}}{{t}^{\mathrm{3}} } \\ $$$$=\:\underset{{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{6}−\mathrm{6sec}\:^{\mathrm{2}} \mathrm{3}{t}}{\mathrm{3}{t}^{\mathrm{2}} }\:=\:\underset{{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{2}\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{cos}\:^{\mathrm{2}} \mathrm{3}{t}}\right)}{{t}^{\mathrm{2}} } \\ $$$$=\mathrm{2}×\:\underset{{t}\rightarrow\mathrm{0}\:} {\mathrm{lim}}\:\frac{\mathrm{cos}\:^{\mathrm{2}} \mathrm{3}{t}−\mathrm{1}}{{t}^{\mathrm{2}} \:\mathrm{cos}\:^{\mathrm{2}} \mathrm{3}{t}}\:=\:\mathrm{2}×\underset{{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{1}}{\mathrm{cos}\:^{\mathrm{2}} \mathrm{3}{t}}\:×\:\underset{{t}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{−\mathrm{sin}\:^{\mathrm{2}} \mathrm{3}{t}}{{t}^{\mathrm{2}} } \\ $$$$=\:\mathrm{2}\:×\:\mathrm{1}\:×\:\left(−\mathrm{9}\right)\:=\:−\mathrm{18} \\ $$
Answered by Henri Boucatchou last updated on 22/Feb/20
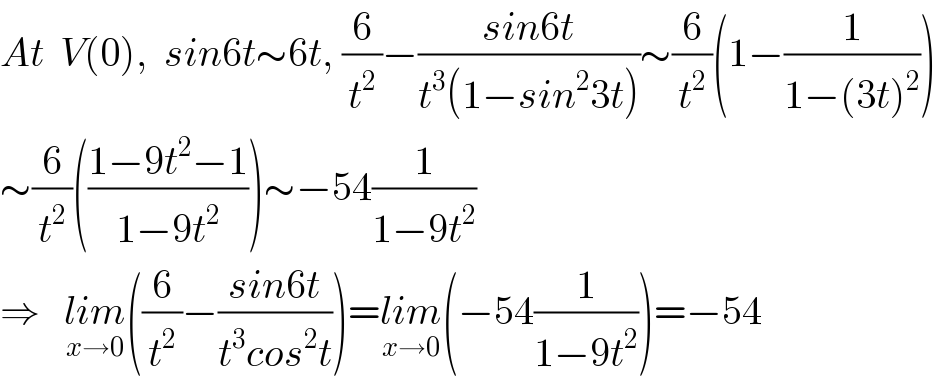
At V(0), sin6t∼6t, (6/t^2 )−((sin6t)/(t^3 (1−sin^2 3t)))∼(6/t^2 )(1−(1/(1−(3t)^2 ))) ∼(6/t^2 )(((1−9t^2 −1)/(1−9t^2 )))∼−54(1/(1−9t^2 )) ⇒ lim_(x→0) ((6/t^2 )−((sin6t)/(t^3 cos^2 t)))=lim_(x→0) (−54(1/(1−9t^2 )))=−54
$${At}\:\:{V}\left(\mathrm{0}\right),\:\:{sin}\mathrm{6}{t}\sim\mathrm{6}{t},\:\frac{\mathrm{6}}{{t}^{\mathrm{2}} }−\frac{{sin}\mathrm{6}{t}}{{t}^{\mathrm{3}} \left(\mathrm{1}−{sin}^{\mathrm{2}} \mathrm{3}{t}\right)}\sim\frac{\mathrm{6}}{{t}^{\mathrm{2}} }\left(\mathrm{1}−\frac{\mathrm{1}}{\mathrm{1}−\left(\mathrm{3}{t}\right)^{\mathrm{2}} }\right) \\ $$$$\sim\frac{\mathrm{6}}{{t}^{\mathrm{2}} }\left(\frac{\mathrm{1}−\mathrm{9}{t}^{\mathrm{2}} −\mathrm{1}}{\mathrm{1}−\mathrm{9}{t}^{\mathrm{2}} }\right)\sim−\mathrm{54}\frac{\mathrm{1}}{\mathrm{1}−\mathrm{9}{t}^{\mathrm{2}} } \\ $$$$\Rightarrow\:\:\:\underset{{x}\rightarrow\mathrm{0}} {{lim}}\left(\frac{\mathrm{6}}{{t}^{\mathrm{2}} }−\frac{{sin}\mathrm{6}{t}}{{t}^{\mathrm{3}} {cos}^{\mathrm{2}} {t}}\right)=\underset{{x}\rightarrow\mathrm{0}} {{lim}}\left(−\mathrm{54}\frac{\mathrm{1}}{\mathrm{1}−\mathrm{9}{t}^{\mathrm{2}} }\right)=−\mathrm{54} \\ $$
Commented by john santu last updated on 22/Feb/20
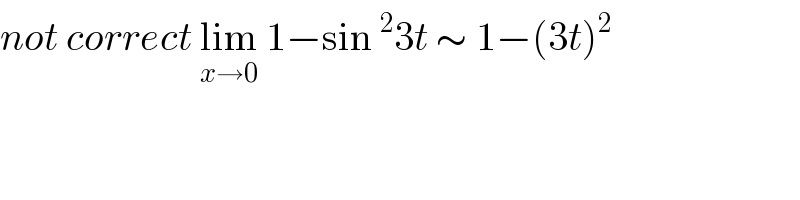
not correct lim_(x→0) 1−sin^2 3t ∼ 1−(3t)^2
$${not}\:{correct}\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\mathrm{1}−\mathrm{sin}\:^{\mathrm{2}} \mathrm{3}{t}\:\sim\:\mathrm{1}−\left(\mathrm{3}{t}\right)^{\mathrm{2}} \\ $$
Commented by Henri Boucatchou last updated on 22/Feb/20
Sorry, take t=x
$${Sorry},\:{take}\:{t}={x} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *