Question Number 82499 by Maclaurin Stickket last updated on 21/Feb/20
Commented by Maclaurin Stickket last updated on 21/Feb/20

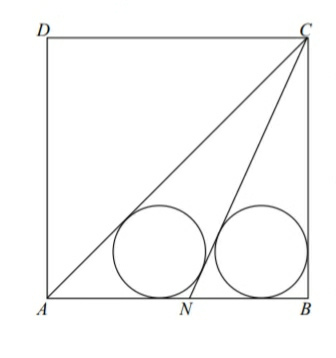
$${ABCD}\:{is}\:{a}\:{square}\:{with}\:{side}\:\mathrm{1}. \\ $$$${The}\:{circles}\:{are}\:{congruent}. \\ $$$${AC}\:{is}\:{the}\:{diagonal}\:{of}\:{square}. \\ $$$${Find}\:{the}\:{radius}\:{r}. \\ $$
Commented by Maclaurin Stickket last updated on 21/Feb/20
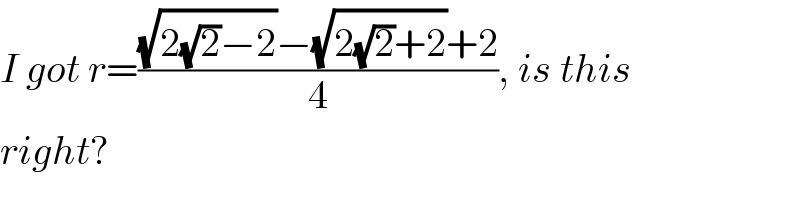
$${I}\:{got}\:{r}=\frac{\sqrt{\mathrm{2}\sqrt{\mathrm{2}}−\mathrm{2}}−\sqrt{\mathrm{2}\sqrt{\mathrm{2}}+\mathrm{2}}+\mathrm{2}}{\mathrm{4}},\:{is}\:{this} \\ $$$${right}? \\ $$
Commented by mr W last updated on 26/Feb/20

$$\sqrt{\mathrm{2}\sqrt{\mathrm{2}}+\mathrm{2}}−\sqrt{\mathrm{2}\sqrt{\mathrm{2}}−\mathrm{2}}=\mathrm{2}\sqrt{\sqrt{\mathrm{2}}−\mathrm{1}} \\ $$$${r}=\frac{\sqrt{\mathrm{2}\sqrt{\mathrm{2}}−\mathrm{2}}−\sqrt{\mathrm{2}\sqrt{\mathrm{2}}+\mathrm{2}}+\mathrm{2}}{\mathrm{4}}=\frac{\mathrm{2}−\mathrm{2}\sqrt{\sqrt{\mathrm{2}}−\mathrm{1}}}{\mathrm{4}} \\ $$$$=\frac{\mathrm{1}−\sqrt{\sqrt{\mathrm{2}}−\mathrm{1}}}{\mathrm{2}} \\ $$
Answered by mr W last updated on 22/Feb/20

Commented by mr W last updated on 26/Feb/20

$$\left(\mathrm{1}−\frac{\mathrm{2}{r}}{{h}}\right)^{\mathrm{2}} =\mathrm{1}−\frac{\mathrm{2}{R}}{{h}} \\ $$$${h}=\mathrm{1} \\ $$$${R}\left(\mathrm{2}+\sqrt{\mathrm{2}}\right)=\mathrm{1} \\ $$$${R}=\frac{\mathrm{2}−\sqrt{\mathrm{2}}}{\mathrm{2}} \\ $$$$\left(\mathrm{1}−\mathrm{2}{r}\right)^{\mathrm{2}} =\sqrt{\mathrm{2}}−\mathrm{1} \\ $$$$\Rightarrow{r}=\frac{\mathrm{1}−\sqrt{\sqrt{\mathrm{2}}−\mathrm{1}}}{\mathrm{2}}\approx\mathrm{0}.\mathrm{178} \\ $$
