Menu Close

Question-82520

Tinku Tara 0 Comments
Pin




Question Number 82520 by peter frank last updated on 22/Feb/20
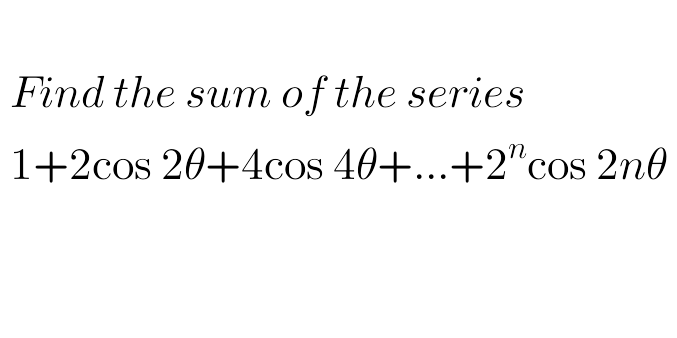
Commented by mathmax by abdo last updated on 22/Feb/20
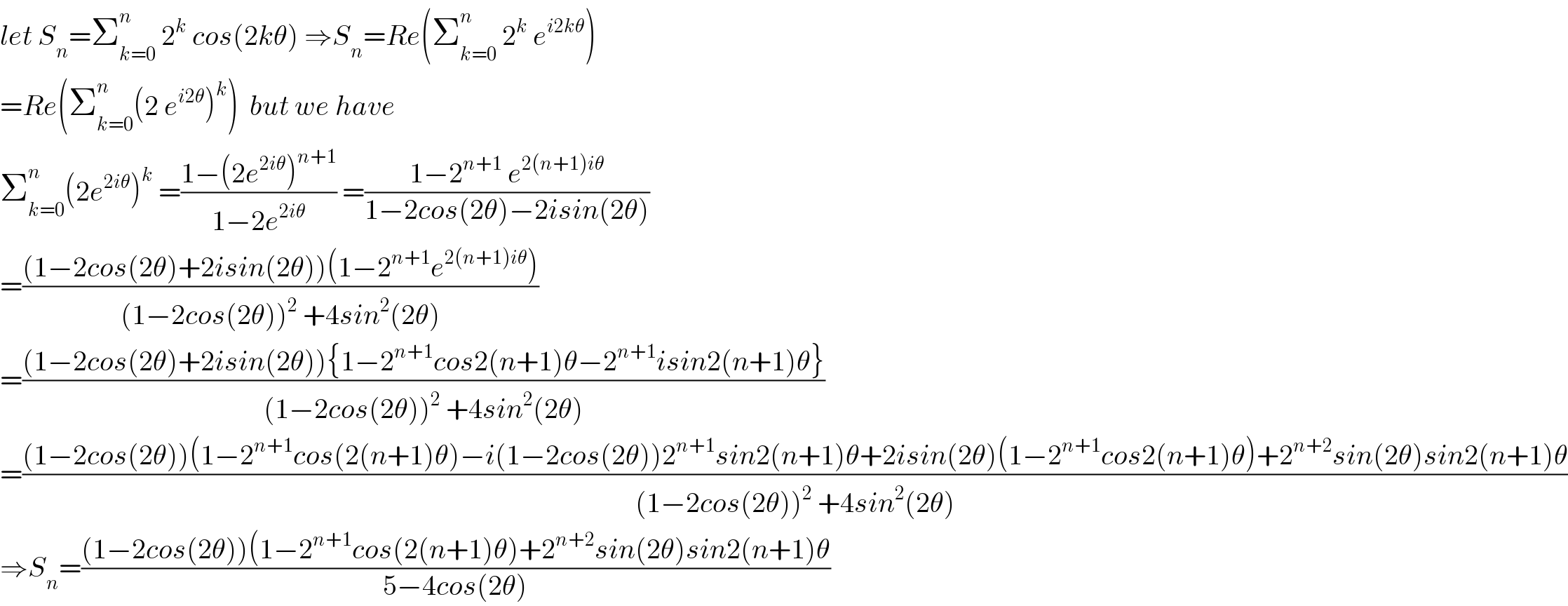
let S_n =Σ_(k=0) ^n 2^k cos(2kθ) ⇒S_n =Re(Σ_(k=0) ^n 2^k e^(i2kθ) ) =Re(Σ_(k=0) ^n (2 e^(i2θ) )^k ) but we have Σ_(k=0) ^n (2e^(2iθ) )^k =((1−(2e^(2iθ) )^(n+1) )/(1−2e^(2iθ) )) =((1−2^(n+1) e^(2(n+1)iθ) )/(1−2cos(2θ)−2isin(2θ))) =(((1−2cos(2θ)+2isin(2θ))(1−2^(n+1) e^(2(n+1)iθ) ))/((1−2cos(2θ))^2 +4sin^2 (2θ))) =(((1−2cos(2θ)+2isin(2θ)){1−2^(n+1) cos2(n+1)θ−2^(n+1) isin2(n+1)θ})/((1−2cos(2θ))^2 +4sin^2 (2θ))) =(((1−2cos(2θ))(1−2^(n+1) cos(2(n+1)θ)−i(1−2cos(2θ))2^(n+1) sin2(n+1)θ+2isin(2θ)(1−2^(n+1) cos2(n+1)θ)+2^(n+2) sin(2θ)sin2(n+1)θ)/((1−2cos(2θ))^2 +4sin^2 (2θ))) ⇒S_n =(((1−2cos(2θ))(1−2^(n+1) cos(2(n+1)θ)+2^(n+2) sin(2θ)sin2(n+1)θ)/(5−4cos(2θ)))
$${let}\:{S}_{{n}} =\sum_{{k}=\mathrm{0}} ^{{n}} \:\mathrm{2}^{{k}} \:{cos}\left(\mathrm{2}{k}\theta\right)\:\Rightarrow{S}_{{n}} ={Re}\left(\sum_{{k}=\mathrm{0}} ^{{n}} \:\mathrm{2}^{{k}} \:{e}^{{i}\mathrm{2}{k}\theta} \right) \\ $$$$={Re}\left(\sum_{{k}=\mathrm{0}} ^{{n}} \left(\mathrm{2}\:{e}^{{i}\mathrm{2}\theta} \right)^{{k}} \right)\:\:{but}\:{we}\:{have} \\ $$$$\sum_{{k}=\mathrm{0}} ^{{n}} \left(\mathrm{2}{e}^{\mathrm{2}{i}\theta} \right)^{{k}} \:=\frac{\mathrm{1}−\left(\mathrm{2}{e}^{\mathrm{2}{i}\theta} \right)^{{n}+\mathrm{1}} }{\mathrm{1}−\mathrm{2}{e}^{\mathrm{2}{i}\theta} }\:=\frac{\mathrm{1}−\mathrm{2}^{{n}+\mathrm{1}} \:{e}^{\mathrm{2}\left({n}+\mathrm{1}\right){i}\theta} }{\mathrm{1}−\mathrm{2}{cos}\left(\mathrm{2}\theta\right)−\mathrm{2}{isin}\left(\mathrm{2}\theta\right)} \\ $$$$=\frac{\left(\mathrm{1}−\mathrm{2}{cos}\left(\mathrm{2}\theta\right)+\mathrm{2}{isin}\left(\mathrm{2}\theta\right)\right)\left(\mathrm{1}−\mathrm{2}^{{n}+\mathrm{1}} {e}^{\mathrm{2}\left({n}+\mathrm{1}\right){i}\theta} \right)}{\left(\mathrm{1}−\mathrm{2}{cos}\left(\mathrm{2}\theta\right)\right)^{\mathrm{2}} \:+\mathrm{4}{sin}^{\mathrm{2}} \left(\mathrm{2}\theta\right)} \\ $$$$=\frac{\left(\mathrm{1}−\mathrm{2}{cos}\left(\mathrm{2}\theta\right)+\mathrm{2}{isin}\left(\mathrm{2}\theta\right)\right)\left\{\mathrm{1}−\mathrm{2}^{{n}+\mathrm{1}} {cos}\mathrm{2}\left({n}+\mathrm{1}\right)\theta−\mathrm{2}^{{n}+\mathrm{1}} {isin}\mathrm{2}\left({n}+\mathrm{1}\right)\theta\right\}}{\left(\mathrm{1}−\mathrm{2}{cos}\left(\mathrm{2}\theta\right)\right)^{\mathrm{2}} \:+\mathrm{4}{sin}^{\mathrm{2}} \left(\mathrm{2}\theta\right)} \\ $$$$=\frac{\left(\mathrm{1}−\mathrm{2}{cos}\left(\mathrm{2}\theta\right)\right)\left(\mathrm{1}−\mathrm{2}^{{n}+\mathrm{1}} {cos}\left(\mathrm{2}\left({n}+\mathrm{1}\right)\theta\right)−{i}\left(\mathrm{1}−\mathrm{2}{cos}\left(\mathrm{2}\theta\right)\right)\mathrm{2}^{{n}+\mathrm{1}} {sin}\mathrm{2}\left({n}+\mathrm{1}\right)\theta+\mathrm{2}{isin}\left(\mathrm{2}\theta\right)\left(\mathrm{1}−\mathrm{2}^{{n}+\mathrm{1}} {cos}\mathrm{2}\left({n}+\mathrm{1}\right)\theta\right)+\mathrm{2}^{{n}+\mathrm{2}} {sin}\left(\mathrm{2}\theta\right){sin}\mathrm{2}\left({n}+\mathrm{1}\right)\theta\right.}{\left(\mathrm{1}−\mathrm{2}{cos}\left(\mathrm{2}\theta\right)\right)^{\mathrm{2}} \:+\mathrm{4}{sin}^{\mathrm{2}} \left(\mathrm{2}\theta\right)} \\ $$$$\Rightarrow{S}_{{n}} =\frac{\left(\mathrm{1}−\mathrm{2}{cos}\left(\mathrm{2}\theta\right)\right)\left(\mathrm{1}−\mathrm{2}^{{n}+\mathrm{1}} {cos}\left(\mathrm{2}\left({n}+\mathrm{1}\right)\theta\right)+\mathrm{2}^{{n}+\mathrm{2}} {sin}\left(\mathrm{2}\theta\right){sin}\mathrm{2}\left({n}+\mathrm{1}\right)\theta\right.}{\mathrm{5}−\mathrm{4}{cos}\left(\mathrm{2}\theta\right)} \\ $$
Answered by mr W last updated on 22/Feb/20
z=2(cos θ+i sin θ)=2e^(iθ) z^k =2^k (cos kθ+i sin kθ)=(2e^(iθ) )^k z^0 +z^1 +z^2 +...+z^n =Σ_(k=0) ^n (2e^(iθ) )^k ← sum of GP Σ_(k=0) ^n 2^k cos (kθ)+iΣ_(k=0) ^n 2^k sin (kθ)=(((2e^(iθ) )^(n+1) −1)/(2e^(iθ) −1)) Σ_(k=0) ^n 2^k cos (kθ)+iΣ_(k=0) ^n 2^k sin (kθ)=((2^(n+1) e^(i(n+1)θ) −1)/(2e^(iθ) −1)) Σ_(k=0) ^n 2^k cos (kθ)+iΣ_(k=0) ^n 2^k sin (kθ)=((2^(n+1) [cos (n+1)θ+i sin (n+1)θ]−1)/(2(cos θ+i sin θ)−1)) Σ_(k=0) ^n 2^k cos (kθ)+iΣ_(k=0) ^n 2^k sin (kθ)=(({[2^(n+1) cos (n+1)θ−1]+i [2^(n+1) sin (n+1)θ]}[(2cos θ−1)−i sin θ])/([(2cos θ−1)+i sin θ][(2cos θ−1)−i sin θ])) Σ_(k=0) ^n 2^k cos (kθ)+iΣ_(k=0) ^n 2^k sin (kθ)=(({[2^(n+1) cos (n+1)θ−1](2cos θ−1)+2^(n+1) sin (n+1)θ sin θ}+i {[2^(n+1) sin (n+1)θ](2cos θ−1)−[2^(n+1) cos (n+1)θ−1]sin θ})/((2cos θ−1)^2 +sin^2 θ)) ⇒Σ_(k=0) ^n 2^k cos (kθ)=(([2^(n+1) cos (n+1)θ−1](2cos θ−1)+2^(n+1) sin θ sin (n+1)θ)/((2cos θ−1)^2 +sin^2 θ)) ⇒Σ_(k=0) ^n 2^k sin (kθ)=((2^(n+1) (2 cos θ−1) sin (n+1)θ−[2^(n+1) cos (n+1)θ−1]sin θ)/((2cos θ−1)^2 +sin^2 θ))
$${z}=\mathrm{2}\left(\mathrm{cos}\:\theta+{i}\:\mathrm{sin}\:\theta\right)=\mathrm{2}{e}^{{i}\theta} \\ $$$${z}^{{k}} =\mathrm{2}^{{k}} \left(\mathrm{cos}\:{k}\theta+{i}\:\mathrm{sin}\:{k}\theta\right)=\left(\mathrm{2}{e}^{{i}\theta} \right)^{{k}} \\ $$$${z}^{\mathrm{0}} +{z}^{\mathrm{1}} +{z}^{\mathrm{2}} +…+{z}^{{n}} =\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\left(\mathrm{2}{e}^{{i}\theta} \right)^{{k}} \:\leftarrow\:{sum}\:{of}\:{GP} \\ $$$$\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\mathrm{2}^{{k}} \mathrm{cos}\:\left({k}\theta\right)+{i}\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\mathrm{2}^{{k}} \mathrm{sin}\:\left({k}\theta\right)=\frac{\left(\mathrm{2}{e}^{{i}\theta} \right)^{{n}+\mathrm{1}} −\mathrm{1}}{\mathrm{2}{e}^{{i}\theta} −\mathrm{1}} \\ $$$$\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\mathrm{2}^{{k}} \mathrm{cos}\:\left({k}\theta\right)+{i}\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\mathrm{2}^{{k}} \mathrm{sin}\:\left({k}\theta\right)=\frac{\mathrm{2}^{{n}+\mathrm{1}} {e}^{{i}\left({n}+\mathrm{1}\right)\theta} −\mathrm{1}}{\mathrm{2}{e}^{{i}\theta} −\mathrm{1}} \\ $$$$\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\mathrm{2}^{{k}} \mathrm{cos}\:\left({k}\theta\right)+{i}\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\mathrm{2}^{{k}} \mathrm{sin}\:\left({k}\theta\right)=\frac{\mathrm{2}^{{n}+\mathrm{1}} \left[\mathrm{cos}\:\left({n}+\mathrm{1}\right)\theta+{i}\:\mathrm{sin}\:\left({n}+\mathrm{1}\right)\theta\right]−\mathrm{1}}{\mathrm{2}\left(\mathrm{cos}\:\theta+{i}\:\mathrm{sin}\:\theta\right)−\mathrm{1}} \\ $$$$\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\mathrm{2}^{{k}} \mathrm{cos}\:\left({k}\theta\right)+{i}\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\mathrm{2}^{{k}} \mathrm{sin}\:\left({k}\theta\right)=\frac{\left\{\left[\mathrm{2}^{{n}+\mathrm{1}} \mathrm{cos}\:\left({n}+\mathrm{1}\right)\theta−\mathrm{1}\right]+{i}\:\left[\mathrm{2}^{{n}+\mathrm{1}} \mathrm{sin}\:\left({n}+\mathrm{1}\right)\theta\right]\right\}\left[\left(\mathrm{2cos}\:\theta−\mathrm{1}\right)−{i}\:\mathrm{sin}\:\theta\right]}{\left[\left(\mathrm{2cos}\:\theta−\mathrm{1}\right)+{i}\:\mathrm{sin}\:\theta\right]\left[\left(\mathrm{2cos}\:\theta−\mathrm{1}\right)−{i}\:\mathrm{sin}\:\theta\right]} \\ $$$$\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\mathrm{2}^{{k}} \mathrm{cos}\:\left({k}\theta\right)+{i}\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\mathrm{2}^{{k}} \mathrm{sin}\:\left({k}\theta\right)=\frac{\left\{\left[\mathrm{2}^{{n}+\mathrm{1}} \mathrm{cos}\:\left({n}+\mathrm{1}\right)\theta−\mathrm{1}\right]\left(\mathrm{2cos}\:\theta−\mathrm{1}\right)+\mathrm{2}^{{n}+\mathrm{1}} \mathrm{sin}\:\left({n}+\mathrm{1}\right)\theta\:\mathrm{sin}\:\theta\right\}+{i}\:\left\{\left[\mathrm{2}^{{n}+\mathrm{1}} \mathrm{sin}\:\left({n}+\mathrm{1}\right)\theta\right]\left(\mathrm{2cos}\:\theta−\mathrm{1}\right)−\left[\mathrm{2}^{{n}+\mathrm{1}} \mathrm{cos}\:\left({n}+\mathrm{1}\right)\theta−\mathrm{1}\right]\mathrm{sin}\:\theta\right\}}{\left(\mathrm{2cos}\:\theta−\mathrm{1}\right)^{\mathrm{2}} +\mathrm{sin}^{\mathrm{2}} \:\theta} \\ $$$$\Rightarrow\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\mathrm{2}^{{k}} \mathrm{cos}\:\left({k}\theta\right)=\frac{\left[\mathrm{2}^{{n}+\mathrm{1}} \mathrm{cos}\:\left({n}+\mathrm{1}\right)\theta−\mathrm{1}\right]\left(\mathrm{2cos}\:\theta−\mathrm{1}\right)+\mathrm{2}^{{n}+\mathrm{1}} \mathrm{sin}\:\theta\:\mathrm{sin}\:\left({n}+\mathrm{1}\right)\theta}{\left(\mathrm{2cos}\:\theta−\mathrm{1}\right)^{\mathrm{2}} +\mathrm{sin}^{\mathrm{2}} \:\theta} \\ $$$$ \\ $$$$\Rightarrow\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}\mathrm{2}^{{k}} \mathrm{sin}\:\left({k}\theta\right)=\frac{\mathrm{2}^{{n}+\mathrm{1}} \left(\mathrm{2}\:\mathrm{cos}\:\theta−\mathrm{1}\right)\:\mathrm{sin}\:\left({n}+\mathrm{1}\right)\theta−\left[\mathrm{2}^{{n}+\mathrm{1}} \mathrm{cos}\:\left({n}+\mathrm{1}\right)\theta−\mathrm{1}\right]\mathrm{sin}\:\theta}{\left(\mathrm{2cos}\:\theta−\mathrm{1}\right)^{\mathrm{2}} +\mathrm{sin}^{\mathrm{2}} \:\theta} \\ $$
Commented by peter frank last updated on 22/Feb/20
thank you very much
$${thank}\:{you}\:{very}\:{much} \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *