Question Number 82531 by Power last updated on 22/Feb/20

Commented by abdomathmax last updated on 24/Feb/20

$${I}\:=\int\:\frac{\sqrt{\mathrm{1}−{x}}}{{x}}{dx}\:+\int\:\frac{\sqrt{\mathrm{2}−{x}^{\mathrm{2}} }}{{x}}{dx}\:+\int\:\:\frac{\sqrt{\mathrm{4}−{x}^{\mathrm{4}} }}{{x}}{dx}\:{we}\:{have} \\ $$$$\int\:\:\frac{\sqrt{\mathrm{1}−{x}}}{{x}}{dx}\:\:{changement}\:\sqrt{\mathrm{1}−{x}}={t}\:{give}\mathrm{1}−{x}={t}^{\mathrm{2}} \:\Rightarrow \\ $$$${x}=\mathrm{1}−{t}^{\mathrm{2}} \:\Rightarrow\int\:\:\frac{\sqrt{\mathrm{1}−{x}}}{{x}}{dx}\:=\:\int\:\:\frac{{t}}{\mathrm{1}−{t}^{\mathrm{2}} }\left(−\mathrm{2}{t}\right){dt} \\ $$$$=\int\:\:\:\frac{\mathrm{2}{t}^{\mathrm{2}} }{{t}^{\mathrm{2}} −\mathrm{1}}{dt}\:=\mathrm{2}\int\:\frac{{t}^{\mathrm{2}} −\mathrm{1}+\mathrm{1}}{{t}^{\mathrm{2}} −\mathrm{1}}{dt}\:=\mathrm{2}\int\:{dt}\:+\mathrm{2}\int\:\:\frac{{dt}}{{t}^{\mathrm{2}} −\mathrm{1}} \\ $$$$=\mathrm{2}{t}\:+\int\:\left(\frac{\mathrm{1}}{{t}−\mathrm{1}}−\frac{\mathrm{1}}{{t}+\mathrm{1}}\right){dt}\:=\mathrm{2}{t}+{ln}\mid\frac{{t}−\mathrm{1}}{{t}+\mathrm{1}}\mid\:+{c} \\ $$$$=\mathrm{2}\sqrt{\mathrm{1}−{x}}+{ln}\mid\frac{\sqrt{\mathrm{1}−{x}}−\mathrm{1}}{\:\sqrt{\mathrm{1}−{x}}+\mathrm{1}}\mid\:+{c} \\ $$$$\int\:\:\frac{\sqrt{\mathrm{2}−{x}^{\mathrm{2}} }}{{x}}{dx}\:=_{{x}=\sqrt{\mathrm{2}}{sint}} \:\:\int\:\:\:\frac{\sqrt{\mathrm{2}}{cost}}{\:\sqrt{\mathrm{2}}{sint}}×\sqrt{\mathrm{2}}{costdt} \\ $$$$=\sqrt{\mathrm{2}}\int\:\:\frac{{cos}^{\mathrm{2}} {t}}{{sint}}{dt}\:=\sqrt{\mathrm{2}}\int\:\:\frac{\mathrm{1}−{sin}^{\mathrm{2}} {t}}{{sint}}{dt} \\ $$$$=\sqrt{\mathrm{2}}\int\:\:\:\frac{{dt}}{{sint}}−\sqrt{\mathrm{2}}\int\:\:{sint}\:{dt}\:\:\:\: \\ $$$$=_{{tan}\left(\frac{{t}}{\mathrm{2}}\right)={u}} \:\:\sqrt{\mathrm{2}}\int\:\:\frac{\mathrm{1}}{\frac{\mathrm{2}{u}}{\mathrm{1}+{u}^{\mathrm{2}} }}×\frac{\mathrm{2}{du}}{\mathrm{1}+{u}^{\mathrm{2}} }\:+\sqrt{\mathrm{2}}{cost}\:\:+{c}^{'} \\ $$$$=\sqrt{\mathrm{2}}{ln}\mid{tan}\left(\frac{{t}}{\mathrm{2}}\right)\mid+\sqrt{\mathrm{2}}\sqrt{\mathrm{1}−\left(\frac{{x}}{\:\sqrt{\mathrm{2}}}\right)^{\mathrm{2}} }\:+{c}^{'} \\ $$$$=\sqrt{\mathrm{2}}{ln}\mid{tan}\left(\frac{\mathrm{1}}{\mathrm{2}}{arcsin}\left(\frac{{x}}{\:\sqrt{\mathrm{2}}}\right)\right)\mid+\sqrt{\mathrm{2}}\sqrt{\mathrm{1}−\frac{{x}^{\mathrm{2}} }{\mathrm{2}}}\:+{c} \\ $$$$….{be}\:{continued}… \\ $$
Answered by TANMAY PANACEA last updated on 22/Feb/20
![∫((1−x)/(x(√(1−x))))dx+∫((2−x^2 )/(x(√(2−x^2 ))))dx+∫((4−x^4 )/(x(√(4−x^4 ))))dx I_1 =∫((1−x)/(x(√(1−x^2 ))))dx t^2 =1−x 2tdt=−dx ∫(t^2 /((1−t^2 )t))×−2tdt 2∫((1−t^2 −1)/(1−t^2 ))dt 2∫dt−2∫(dt/(1−t^2 )) 2∫dt−[∫(dt/(1+t))+∫(dt/(1−t))] 2∫dt−∫(dt/(1+t))+∫(dt/(t−1)) 2t+ln(((t−1)/(t+1)))+c_1 (√(1−x)) +ln((((√(1−x)) −1)/( (√(1−x)) +1)))+c_1 I_2 =∫((2−x^2 )/(x(√(2−x^2 )))) 2∫((xdx)/(x^2 (√(2−x^2 ))))−∫((xdx)/( (√(2−x^2 )))) k^2 =2−x^2 →kdk=−xdx 2∫((−kdk)/((2−k^2 )))+∫((kdk)/k) ∫((d(2−k^2 ))/(2−k^2 ))+∫dk ln(2−k^2 )+k+c_2 ln(x^2 )+(√(2−x^2 )) +c_2 I_3 =∫((4−x^4 )/(x(√(4−x^4 ))))dx ∫((4xdx)/(x^2 (√(4−x^4 ))))−∫(x^3 /( (√(4−x^4 ))))dx 2∫((d(x^2 ))/(x^2 (√(4−x^4 ))))−(1/2)∫((x^2 ×d(x^2 ))/( (√(4−x^4 )))) 2∫(dp/(p(√(4−p^2 ))))−(1/2)∫((pdp)/( (√(4−p^2 )))) [ p=x^2 ] 2∫((pdp)/(p^2 (√(4−p^2 ))))−(1/2)∫((pdp)/( (√(4−p^2 )))) a^2 =4−p^2 →2ada=−2pdp★ [a^2 =4−p^2 =4−x^4 ] 2∫((−ada)/((4−a^2 )a))−(1/2)∫((−ada)/a) −2∫(da/((2+a)(2−a)))+(1/2)∫da ((−1)/2)∫((2+a+2−a)/((2+a)(2−a)))da+(1/2)∫da ((−1)/2)∫(da/(2−a))−(1/2)∫(da/(2+a))+(1/2)∫da (1/2)∫(da/(a−2))−(1/2)∫(da/(a+2))+(1/2)∫da (1/2)ln(((a−2)/(a+2)))+(a/2)+c_3 (1/2)ln((((√(4−x^4 )) −2)/( (√(4−x^4 )) +2)))+((√(4−x^4 ))/2)+c_3](https://www.tinkutara.com/question/Q82544.png)
$$\int\frac{\mathrm{1}−{x}}{{x}\sqrt{\mathrm{1}−{x}}}{dx}+\int\frac{\mathrm{2}−{x}^{\mathrm{2}} }{{x}\sqrt{\mathrm{2}−{x}^{\mathrm{2}} }}{dx}+\int\frac{\mathrm{4}−{x}^{\mathrm{4}} }{{x}\sqrt{\mathrm{4}−{x}^{\mathrm{4}} }}{dx} \\ $$$${I}_{\mathrm{1}} =\int\frac{\mathrm{1}−{x}}{{x}\sqrt{\mathrm{1}−{x}^{\mathrm{2}} }}{dx} \\ $$$${t}^{\mathrm{2}} =\mathrm{1}−{x} \\ $$$$\mathrm{2}{tdt}=−{dx} \\ $$$$\int\frac{{t}^{\mathrm{2}} }{\left(\mathrm{1}−{t}^{\mathrm{2}} \right){t}}×−\mathrm{2}{tdt} \\ $$$$\mathrm{2}\int\frac{\mathrm{1}−{t}^{\mathrm{2}} −\mathrm{1}}{\mathrm{1}−{t}^{\mathrm{2}} }{dt} \\ $$$$\mathrm{2}\int{dt}−\mathrm{2}\int\frac{{dt}}{\mathrm{1}−{t}^{\mathrm{2}} } \\ $$$$\mathrm{2}\int{dt}−\left[\int\frac{{dt}}{\mathrm{1}+{t}}+\int\frac{{dt}}{\mathrm{1}−{t}}\right] \\ $$$$\mathrm{2}\int{dt}−\int\frac{{dt}}{\mathrm{1}+{t}}+\int\frac{{dt}}{{t}−\mathrm{1}} \\ $$$$\mathrm{2}{t}+{ln}\left(\frac{{t}−\mathrm{1}}{{t}+\mathrm{1}}\right)+{c}_{\mathrm{1}} \\ $$$$\sqrt{\mathrm{1}−{x}}\:+{ln}\left(\frac{\sqrt{\mathrm{1}−{x}}\:−\mathrm{1}}{\:\sqrt{\mathrm{1}−{x}}\:+\mathrm{1}}\right)+{c}_{\mathrm{1}} \\ $$$${I}_{\mathrm{2}} =\int\frac{\mathrm{2}−{x}^{\mathrm{2}} }{{x}\sqrt{\mathrm{2}−{x}^{\mathrm{2}} }} \\ $$$$\mathrm{2}\int\frac{{xdx}}{{x}^{\mathrm{2}} \sqrt{\mathrm{2}−{x}^{\mathrm{2}} }}−\int\frac{{xdx}}{\:\sqrt{\mathrm{2}−{x}^{\mathrm{2}} }} \\ $$$${k}^{\mathrm{2}} =\mathrm{2}−{x}^{\mathrm{2}} \rightarrow{kdk}=−{xdx} \\ $$$$\mathrm{2}\int\frac{−{kdk}}{\left(\mathrm{2}−{k}^{\mathrm{2}} \right)}+\int\frac{{kdk}}{{k}} \\ $$$$\int\frac{{d}\left(\mathrm{2}−{k}^{\mathrm{2}} \right)}{\mathrm{2}−{k}^{\mathrm{2}} }+\int{dk} \\ $$$${ln}\left(\mathrm{2}−{k}^{\mathrm{2}} \right)+{k}+{c}_{\mathrm{2}} \\ $$$${ln}\left({x}^{\mathrm{2}} \right)+\sqrt{\mathrm{2}−{x}^{\mathrm{2}} }\:+{c}_{\mathrm{2}} \\ $$$${I}_{\mathrm{3}} =\int\frac{\mathrm{4}−{x}^{\mathrm{4}} }{{x}\sqrt{\mathrm{4}−{x}^{\mathrm{4}} }}{dx} \\ $$$$\int\frac{\mathrm{4}{xdx}}{{x}^{\mathrm{2}} \sqrt{\mathrm{4}−{x}^{\mathrm{4}} }}−\int\frac{{x}^{\mathrm{3}} }{\:\sqrt{\mathrm{4}−{x}^{\mathrm{4}} }}{dx} \\ $$$$\mathrm{2}\int\frac{{d}\left({x}^{\mathrm{2}} \right)}{{x}^{\mathrm{2}} \sqrt{\mathrm{4}−{x}^{\mathrm{4}} }}−\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{x}^{\mathrm{2}} ×{d}\left({x}^{\mathrm{2}} \right)}{\:\sqrt{\mathrm{4}−{x}^{\mathrm{4}} }} \\ $$$$\mathrm{2}\int\frac{{dp}}{{p}\sqrt{\mathrm{4}−{p}^{\mathrm{2}} }}−\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{pdp}}{\:\sqrt{\mathrm{4}−{p}^{\mathrm{2}} }}\:\:\:\:\left[\:{p}={x}^{\mathrm{2}} \right] \\ $$$$\mathrm{2}\int\frac{{pdp}}{{p}^{\mathrm{2}} \sqrt{\mathrm{4}−{p}^{\mathrm{2}} }}−\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{pdp}}{\:\sqrt{\mathrm{4}−{p}^{\mathrm{2}} }} \\ $$$${a}^{\mathrm{2}} =\mathrm{4}−{p}^{\mathrm{2}} \rightarrow\mathrm{2}{ada}=−\mathrm{2}{pdp}\bigstar\:\:\left[{a}^{\mathrm{2}} =\mathrm{4}−{p}^{\mathrm{2}} =\mathrm{4}−{x}^{\mathrm{4}} \right] \\ $$$$\mathrm{2}\int\frac{−{ada}}{\left(\mathrm{4}−{a}^{\mathrm{2}} \right){a}}−\frac{\mathrm{1}}{\mathrm{2}}\int\frac{−{ada}}{{a}} \\ $$$$−\mathrm{2}\int\frac{{da}}{\left(\mathrm{2}+{a}\right)\left(\mathrm{2}−{a}\right)}+\frac{\mathrm{1}}{\mathrm{2}}\int{da} \\ $$$$\frac{−\mathrm{1}}{\mathrm{2}}\int\frac{\mathrm{2}+{a}+\mathrm{2}−{a}}{\left(\mathrm{2}+{a}\right)\left(\mathrm{2}−{a}\right)}{da}+\frac{\mathrm{1}}{\mathrm{2}}\int{da} \\ $$$$\frac{−\mathrm{1}}{\mathrm{2}}\int\frac{{da}}{\mathrm{2}−{a}}−\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{da}}{\mathrm{2}+{a}}+\frac{\mathrm{1}}{\mathrm{2}}\int{da} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{da}}{{a}−\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{2}}\int\frac{{da}}{{a}+\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}\int{da} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}{ln}\left(\frac{{a}−\mathrm{2}}{{a}+\mathrm{2}}\right)+\frac{{a}}{\mathrm{2}}+{c}_{\mathrm{3}} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}{ln}\left(\frac{\sqrt{\mathrm{4}−{x}^{\mathrm{4}} }\:−\mathrm{2}}{\:\sqrt{\mathrm{4}−{x}^{\mathrm{4}} }\:+\mathrm{2}}\right)+\frac{\sqrt{\mathrm{4}−{x}^{\mathrm{4}} }}{\mathrm{2}}+{c}_{\mathrm{3}} \\ $$$$ \\ $$$$ \\ $$$$ \\ $$$$ \\ $$
Commented by peter frank last updated on 22/Feb/20

$${thank}\:{you} \\ $$
Commented by Power last updated on 22/Feb/20

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir} \\ $$
Commented by TANMAY PANACEA last updated on 22/Feb/20
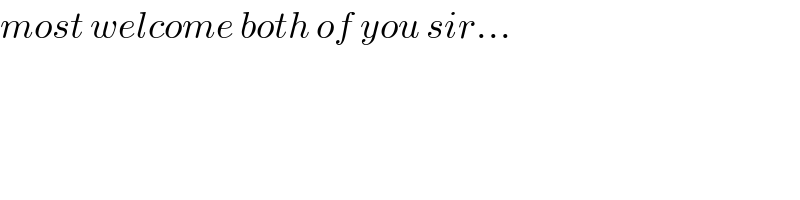
$${most}\:{welcome}\:{both}\:{of}\:{you}\:{sir}… \\ $$
