Question Number 82607 by arthur.kangdani@gmail.com last updated on 23/Feb/20

Commented by jagoll last updated on 23/Feb/20
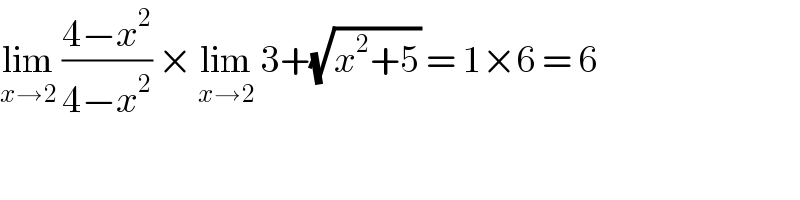
$$\underset{{x}\rightarrow\mathrm{2}} {\mathrm{lim}}\:\frac{\mathrm{4}−{x}^{\mathrm{2}} }{\mathrm{4}−{x}^{\mathrm{2}} }\:×\:\underset{{x}\rightarrow\mathrm{2}} {\mathrm{lim}}\:\mathrm{3}+\sqrt{{x}^{\mathrm{2}} +\mathrm{5}}\:=\:\mathrm{1}×\mathrm{6}\:=\:\mathrm{6} \\ $$
Commented by niroj last updated on 23/Feb/20

$$\:\mathrm{yes}\:\mathrm{my}\:\mathrm{friend}\:\mathrm{your}\:\mathrm{saying}\:\mathrm{true}. \\ $$$$\:\mathrm{its}\:\mathrm{been}\:\mathrm{error}\:\mathrm{by}\:\mathrm{the}\:\mathrm{wrong}\:\mathrm{lim}\: \\ $$$$\:\mathrm{now}\:\mathrm{done}. \\ $$
Commented by jagoll last updated on 23/Feb/20
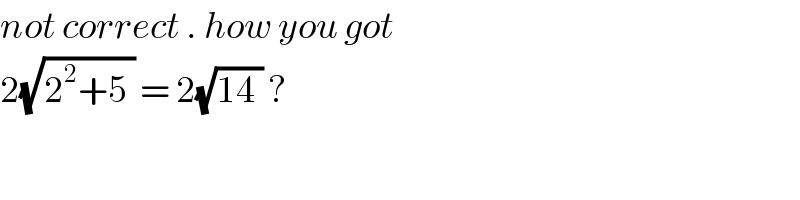
$${not}\:{correct}\:.\:{how}\:{you}\:{got} \\ $$$$\mathrm{2}\sqrt{\mathrm{2}^{\mathrm{2}} +\mathrm{5}\:}\:=\:\mathrm{2}\sqrt{\mathrm{14}\:}\:? \\ $$
Commented by jagoll last updated on 23/Feb/20
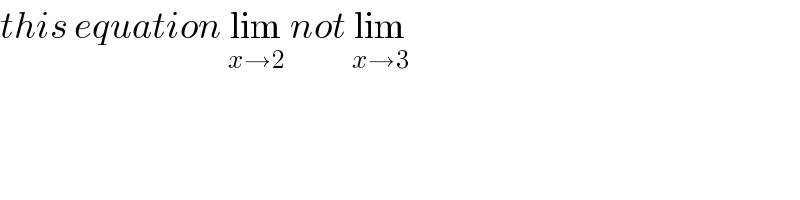
$${this}\:{equation}\:\underset{{x}\rightarrow\mathrm{2}} {\mathrm{lim}}\:{not}\:\underset{{x}\rightarrow\mathrm{3}} {\mathrm{lim}}\: \\ $$
Commented by mathmax by abdo last updated on 23/Feb/20

$$={lim}_{{x}\rightarrow\mathrm{2}} \:\:\:\frac{\left(\mathrm{4}−{x}^{\mathrm{2}} \right)\left(\mathrm{3}+\sqrt{{x}^{\mathrm{2}} \:+\mathrm{5}}\right)}{\mathrm{9}−{x}^{\mathrm{2}} −\mathrm{5}}={lim}_{{x}\rightarrow\mathrm{2}} \:\:\frac{\left(\mathrm{4}−{x}^{\mathrm{2}} \right)\left(\mathrm{3}+\sqrt{{x}^{\mathrm{2}} +\mathrm{5}}\right)}{\mathrm{4}−{x}^{\mathrm{2}} } \\ $$$$={lim}_{{x}\rightarrow\mathrm{2}} \:\:\left(\mathrm{3}+\sqrt{{x}^{\mathrm{2}} +\mathrm{5}}\right)\:=\mathrm{6} \\ $$
Answered by niroj last updated on 23/Feb/20
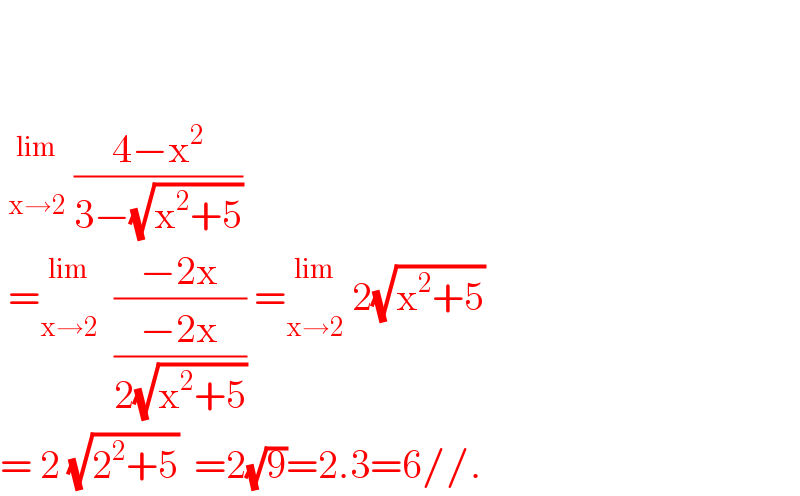
$$ \\ $$$$\:\: \\ $$$$\:\underset{\mathrm{x}\rightarrow\mathrm{2}} {\overset{\mathrm{lim}} {\:}}\:\frac{\mathrm{4}−\mathrm{x}^{\mathrm{2}} }{\mathrm{3}−\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{5}}} \\ $$$$\:=\underset{\mathrm{x}\rightarrow\mathrm{2}} {\overset{\mathrm{lim}} {\:}}\:\:\frac{−\mathrm{2x}}{\frac{−\mathrm{2x}}{\mathrm{2}\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{5}}}}\:=\underset{\mathrm{x}\rightarrow\mathrm{2}} {\overset{\mathrm{lim}} {\:}}\:\mathrm{2}\sqrt{\mathrm{x}^{\mathrm{2}} +\mathrm{5}} \\ $$$$=\:\mathrm{2}\:\sqrt{\mathrm{2}^{\mathrm{2}} +\mathrm{5}}\:\:=\mathrm{2}\sqrt{\mathrm{9}}=\mathrm{2}.\mathrm{3}=\mathrm{6}//. \\ $$
