Menu Close

Question-82726

Tinku Tara 0 Comments
Pin




Question Number 82726 by mr W last updated on 23/Feb/20
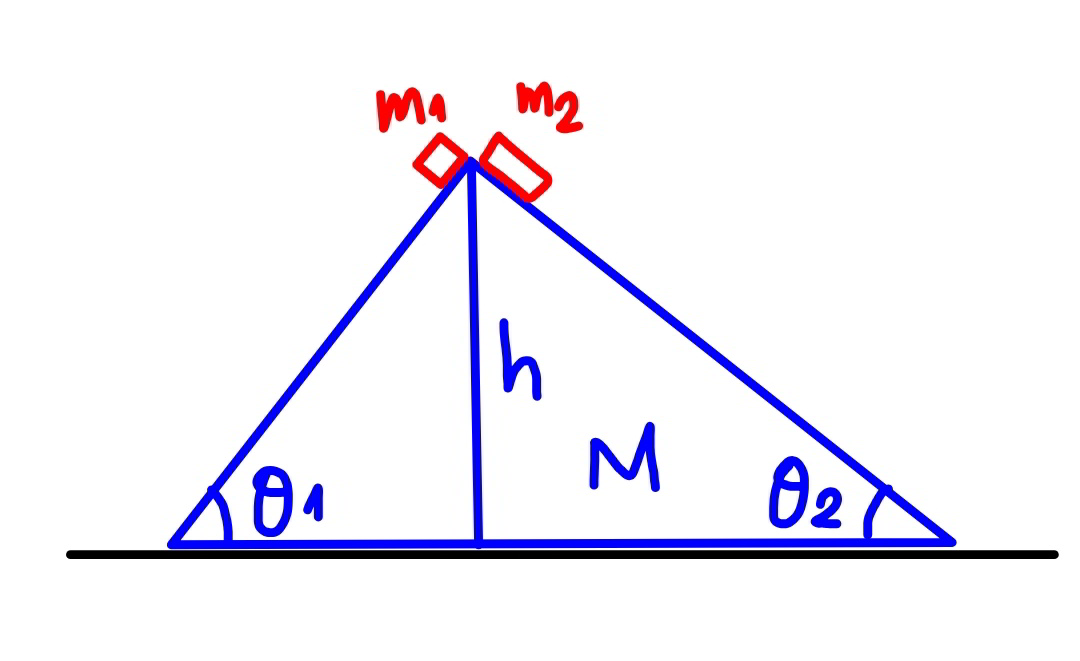
Commented by mr W last updated on 23/Feb/20
mass m_1 and m_2 are released from the top of a wedge simutaneously. assume that mass m_1 reaches the bottum of the wedge firstly. find the velocity of the wedge at this moment. all surfaces are frictionless.
$${mass}\:{m}_{\mathrm{1}} \:{and}\:{m}_{\mathrm{2}} \:{are}\:{released}\:{from}\:{the} \\ $$$${top}\:{of}\:{a}\:{wedge}\:{simutaneously}.\:{assume} \\ $$$${that}\:{mass}\:{m}_{\mathrm{1}} \:{reaches}\:{the}\:{bottum}\:{of} \\ $$$${the}\:{wedge}\:{firstly}.\:{find}\:{the}\:{velocity}\:{of} \\ $$$${the}\:{wedge}\:{at}\:{this}\:{moment}. \\ $$$${all}\:{surfaces}\:{are}\:{frictionless}. \\ $$
Commented by TawaTawa last updated on 23/Feb/20
Sir please i need help, i have post the question several time. i repost now Q82729. Or the question is not correct so that i can stop posting it. Please help. Thanks sir.
$$\mathrm{Sir}\:\mathrm{please}\:\mathrm{i}\:\mathrm{need}\:\mathrm{help},\:\mathrm{i}\:\mathrm{have}\:\mathrm{post}\:\mathrm{the}\:\mathrm{question}\:\mathrm{several}\:\mathrm{time}. \\ $$$$\mathrm{i}\:\mathrm{repost}\:\mathrm{now}\:\:\mathrm{Q82729}.\:\:\mathrm{Or}\:\mathrm{the}\:\mathrm{question}\:\mathrm{is}\:\mathrm{not}\:\mathrm{correct}\:\mathrm{so}\:\mathrm{that}\:\mathrm{i}\:\mathrm{can}\:\mathrm{stop} \\ $$$$\mathrm{posting}\:\mathrm{it}.\:\mathrm{Please}\:\mathrm{help}.\:\mathrm{Thanks}\:\mathrm{sir}.\: \\ $$
Commented by ajfour last updated on 23/Feb/20
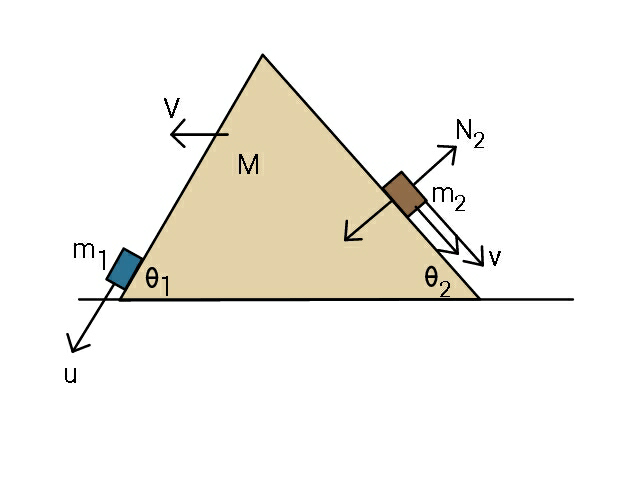
Commented by TawaTawa last updated on 23/Feb/20
Sir, i have typed the question. please check. God bless you sir. Q82729.
$$\mathrm{Sir},\:\mathrm{i}\:\mathrm{have}\:\mathrm{typed}\:\mathrm{the}\:\mathrm{question}.\:\mathrm{please}\:\mathrm{check}.\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}. \\ $$$$\mathrm{Q82729}. \\ $$
Commented by ajfour last updated on 23/Feb/20
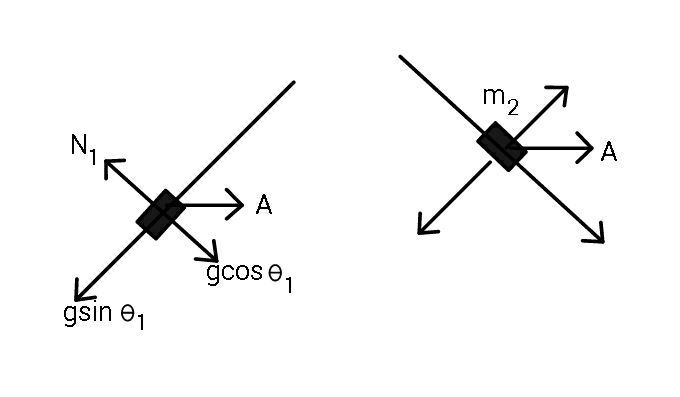
Commented by ajfour last updated on 23/Feb/20
a_1 =gsin θ_1 −Acos θ_1 a_2 =gsin θ_2 +Acos θ_2 (h/(sin θ_1 ))=(1/2)(gsin θ_1 −Acos θ_1 )t^2 ⇒ ((2h)/(sin θ_1 ))=gt^2 sin θ_1 −Vtcos θ_1 ..(i) [ from above eq. we get t(V)] u=(gsin θ_1 −Acos θ_1 )t = gtsin θ_1 −Vcos θ_2 .....(ii) v=gtsin θ_2 +Vcos θ_2 .....(iii) m_1 ucos θ_1 +(M+m_1 +m_2 )V = m_2 vcos θ_2 .....(iv) using (i), (ii), (iii), (iv) V is obtained...
$$\mathrm{a}_{\mathrm{1}} =\mathrm{gsin}\:\theta_{\mathrm{1}} −\mathrm{Acos}\:\theta_{\mathrm{1}} \\ $$$$\mathrm{a}_{\mathrm{2}} =\mathrm{gsin}\:\theta_{\mathrm{2}} +\mathrm{Acos}\:\theta_{\mathrm{2}} \\ $$$$\frac{\mathrm{h}}{\mathrm{sin}\:\theta_{\mathrm{1}} }=\frac{\mathrm{1}}{\mathrm{2}}\left(\mathrm{gsin}\:\theta_{\mathrm{1}} −\mathrm{Acos}\:\theta_{\mathrm{1}} \right)\mathrm{t}^{\mathrm{2}} \\ $$$$\Rightarrow\:\frac{\mathrm{2h}}{\mathrm{sin}\:\theta_{\mathrm{1}} }=\mathrm{gt}^{\mathrm{2}} \mathrm{sin}\:\theta_{\mathrm{1}} −\mathrm{Vtcos}\:\theta_{\mathrm{1}} \:\:..\left(\mathrm{i}\right) \\ $$$$\left[\:\mathrm{from}\:\mathrm{above}\:\mathrm{eq}.\:\mathrm{we}\:\mathrm{get}\:\mathrm{t}\left(\mathrm{V}\right)\right] \\ $$$$\mathrm{u}=\left(\mathrm{gsin}\:\theta_{\mathrm{1}} −\mathrm{Acos}\:\theta_{\mathrm{1}} \right)\mathrm{t} \\ $$$$\:\:\:\:=\:\mathrm{gtsin}\:\theta_{\mathrm{1}} −\mathrm{Vcos}\:\theta_{\mathrm{2}} \:\:\:\:…..\left(\mathrm{ii}\right) \\ $$$$\mathrm{v}=\mathrm{gtsin}\:\theta_{\mathrm{2}} +\mathrm{Vcos}\:\theta_{\mathrm{2}} \:\:\:\:\:\:…..\left(\mathrm{iii}\right) \\ $$$$\mathrm{m}_{\mathrm{1}} \mathrm{ucos}\:\theta_{\mathrm{1}} +\left(\mathrm{M}+\mathrm{m}_{\mathrm{1}} +\mathrm{m}_{\mathrm{2}} \right)\mathrm{V} \\ $$$$\:\:\:\:\:\:\:\:\:=\:\mathrm{m}_{\mathrm{2}} \mathrm{vcos}\:\theta_{\mathrm{2}} \:\:\:\:\:\:\:\:\:\:\:\:\:\:…..\left(\mathrm{iv}\right) \\ $$$$\mathrm{using}\:\left(\mathrm{i}\right),\:\left(\mathrm{ii}\right),\:\left(\mathrm{iii}\right),\:\left(\mathrm{iv}\right) \\ $$$$\mathrm{V}\:\mathrm{is}\:\mathrm{obtained}… \\ $$$$ \\ $$
Commented by mr W last updated on 23/Feb/20
wonderful solution sir! we can get V=((8gh)/(cos θ_1 {((4 tan θ_1 (M+m_1 sin^2 θ_1 +m_2 sin^2 θ_2 ))/(m_2 sin 2θ_2 −m_1 sin 2θ_1 ))−1}^2 −1))
$${wonderful}\:{solution}\:{sir}! \\ $$$${we}\:{can}\:{get} \\ $$$${V}=\frac{\mathrm{8}{gh}}{\mathrm{cos}\:\theta_{\mathrm{1}} \left\{\frac{\mathrm{4}\:\mathrm{tan}\:\theta_{\mathrm{1}} \left(\mathrm{M}+\mathrm{m}_{\mathrm{1}} \mathrm{sin}^{\mathrm{2}} \:\theta_{\mathrm{1}} +\mathrm{m}_{\mathrm{2}} \mathrm{sin}^{\mathrm{2}} \:\theta_{\mathrm{2}} \right)}{{m}_{\mathrm{2}} \mathrm{sin}\:\mathrm{2}\theta_{\mathrm{2}} −{m}_{\mathrm{1}} \mathrm{sin}\:\mathrm{2}\theta_{\mathrm{1}} }−\mathrm{1}\right\}^{\mathrm{2}} −\mathrm{1}} \\ $$
Commented by mr W last updated on 24/Feb/20
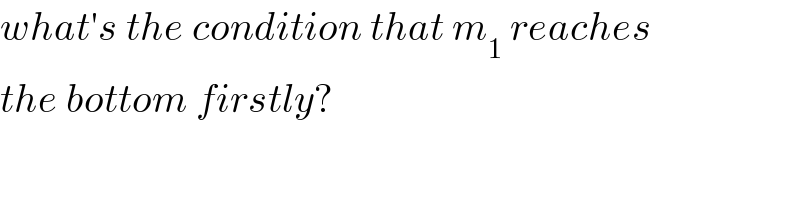
what′s the condition that m_1 reaches the bottom firstly?
$${what}'{s}\:{the}\:{condition}\:{that}\:{m}_{\mathrm{1}} \:{reaches} \\ $$$${the}\:{bottom}\:{firstly}? \\ $$
Commented by ajfour last updated on 24/Feb/20
If t_1 < t_2 , m_1 reaches first. a_1 =gsin θ_1 −Acos θ_1 a_2 =gsin θ_2 +Acos θ_2 (1/2)a_1 t_1 ^2 =(h/(sin θ_1 )) , (1/2)a_2 t_2 ^2 =(h/(sin θ_2 )) t_1 =(√((2h)/(a_1 sin θ_1 ))) , t_2 =(√((2h)/(a_2 sin θ_2 ))) N_1 =m_1 gcos θ_1 +m_1 Asin θ_1 N_2 =m_2 gcos θ_2 −m_2 Asin θ_2 N_2 sin θ_2 −N_1 sin θ_1 =MA A is determined from above 3 eqs. hence we have a_1 , a_2 . Then the condition can be expressed..
$$\mathrm{If}\:\:\:\mathrm{t}_{\mathrm{1}} <\:\mathrm{t}_{\mathrm{2}} \:,\:\:\:\mathrm{m}_{\mathrm{1}} \:\mathrm{reaches}\:\mathrm{first}. \\ $$$$\mathrm{a}_{\mathrm{1}} =\mathrm{gsin}\:\theta_{\mathrm{1}} −\mathrm{Acos}\:\theta_{\mathrm{1}} \\ $$$$\mathrm{a}_{\mathrm{2}} =\mathrm{gsin}\:\theta_{\mathrm{2}} +\mathrm{Acos}\:\theta_{\mathrm{2}} \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\mathrm{a}_{\mathrm{1}} \mathrm{t}_{\mathrm{1}} ^{\mathrm{2}} =\frac{\mathrm{h}}{\mathrm{sin}\:\theta_{\mathrm{1}} }\:\:\:,\:\:\:\frac{\mathrm{1}}{\mathrm{2}}\mathrm{a}_{\mathrm{2}} \mathrm{t}_{\mathrm{2}} ^{\mathrm{2}} =\frac{\mathrm{h}}{\mathrm{sin}\:\theta_{\mathrm{2}} } \\ $$$$\:\:\mathrm{t}_{\mathrm{1}} =\sqrt{\frac{\mathrm{2h}}{\mathrm{a}_{\mathrm{1}} \mathrm{sin}\:\theta_{\mathrm{1}} }}\:,\:\:\mathrm{t}_{\mathrm{2}} =\sqrt{\frac{\mathrm{2h}}{\mathrm{a}_{\mathrm{2}} \mathrm{sin}\:\theta_{\mathrm{2}} }} \\ $$$$\mathrm{N}_{\mathrm{1}} =\mathrm{m}_{\mathrm{1}} \mathrm{gcos}\:\theta_{\mathrm{1}} +\mathrm{m}_{\mathrm{1}} \mathrm{Asin}\:\theta_{\mathrm{1}} \\ $$$$\mathrm{N}_{\mathrm{2}} =\mathrm{m}_{\mathrm{2}} \mathrm{gcos}\:\theta_{\mathrm{2}} −\mathrm{m}_{\mathrm{2}} \mathrm{Asin}\:\theta_{\mathrm{2}} \\ $$$$\mathrm{N}_{\mathrm{2}} \mathrm{sin}\:\theta_{\mathrm{2}} −\mathrm{N}_{\mathrm{1}} \mathrm{sin}\:\theta_{\mathrm{1}} =\mathrm{MA} \\ $$$$\mathrm{A}\:\mathrm{is}\:\mathrm{determined}\:\mathrm{from}\:\mathrm{above}\:\mathrm{3}\:\mathrm{eqs}. \\ $$$$\mathrm{hence}\:\mathrm{we}\:\mathrm{have}\:\mathrm{a}_{\mathrm{1}} \:,\:\mathrm{a}_{\mathrm{2}} . \\ $$$$\mathrm{Then}\:\mathrm{the}\:\mathrm{condition}\:\mathrm{can}\:\mathrm{be} \\ $$$$\mathrm{expressed}.. \\ $$
Commented by mr W last updated on 24/Feb/20
clear! thanks!
$${clear}!\:{thanks}! \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *