Question Number 82729 by TawaTawa last updated on 23/Feb/20

Commented by Kunal12588 last updated on 23/Feb/20

$${In}\:{the}\:\bigtriangleup{ABC},\:{let}\:{G}\:{be}\:{the}\:{centroid},\:{and}\:{let}\:{I} \\ $$$${be}\:{the}\:{center}\:{of}\:{the}\:{inscribed}\:{circle}.\:{Let}\:\alpha \\ $$$${and}\:\beta\:{be}\:{the}\:{angles}\:{at}\:{the}\:{vertices}\:{A}\:{and}\:{B} \\ $$$${respectively}.\:{Suppose}\:{that}\:{the}\:{segment}\:{IG}\:\parallel\:{AB} \\ $$$${and}\:{that}\:\beta\:=\:\mathrm{2}\:{tan}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{3}}\right).\:{Find}\:\alpha. \\ $$
Commented by TawaTawa last updated on 23/Feb/20

$$\mathrm{In}\:\mathrm{the}\:\mathrm{triangle}\:\Delta\mathrm{ABC},\:\mathrm{let}\:\:\mathrm{G}\:\mathrm{be}\:\mathrm{the}\:\mathrm{centroid},\:\mathrm{and}\:\mathrm{let}\:\:\mathrm{I} \\ $$$$\mathrm{be}\:\mathrm{the}\:\mathrm{centre}\:\mathrm{of}\:\mathrm{the}\:\mathrm{inscribed}\:\mathrm{circle}.\:\mathrm{Let}\:\alpha\:\mathrm{and}\:\beta\:\mathrm{be}\:\mathrm{the} \\ $$$$\mathrm{angles}\:\mathrm{at}\:\mathrm{the}\:\mathrm{vertices}\:\mathrm{A}\:\mathrm{and}\:\mathrm{B}\:\mathrm{respectively}.\:\mathrm{Suppose}\:\mathrm{that} \\ $$$$\mathrm{the}\:\mathrm{segment}\:\:\mathrm{IG}\:\:\mathrm{is}\:\mathrm{parallel}\:\mathrm{to}\:\:\mathrm{AB}\:\:\mathrm{and}\:\mathrm{that}\:\:\beta\:\:=\:\:\mathrm{2}\:\mathrm{tan}^{−\mathrm{1}} \left(\frac{\mathrm{1}}{\mathrm{3}}\right). \\ $$$$\mathrm{Find}\:\:\alpha. \\ $$
Answered by mr W last updated on 24/Feb/20

Commented by mr W last updated on 24/Feb/20
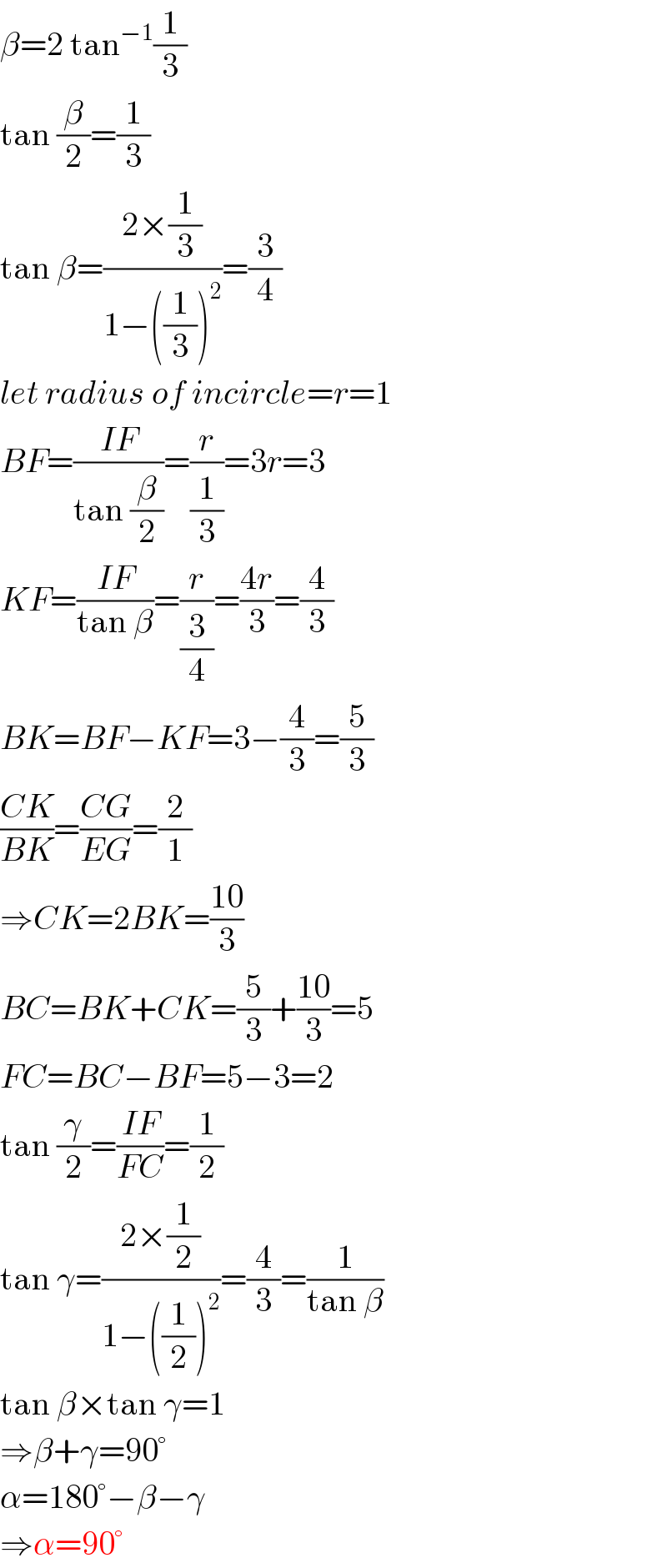
$$\beta=\mathrm{2}\:\mathrm{tan}^{−\mathrm{1}} \frac{\mathrm{1}}{\mathrm{3}} \\ $$$$\mathrm{tan}\:\frac{\beta}{\mathrm{2}}=\frac{\mathrm{1}}{\mathrm{3}} \\ $$$$\mathrm{tan}\:\beta=\frac{\mathrm{2}×\frac{\mathrm{1}}{\mathrm{3}}}{\mathrm{1}−\left(\frac{\mathrm{1}}{\mathrm{3}}\right)^{\mathrm{2}} }=\frac{\mathrm{3}}{\mathrm{4}} \\ $$$${let}\:{radius}\:{of}\:{incircle}={r}=\mathrm{1} \\ $$$${BF}=\frac{{IF}}{\mathrm{tan}\:\frac{\beta}{\mathrm{2}}}=\frac{{r}}{\frac{\mathrm{1}}{\mathrm{3}}}=\mathrm{3}{r}=\mathrm{3} \\ $$$${KF}=\frac{{IF}}{\mathrm{tan}\:\beta}=\frac{{r}}{\frac{\mathrm{3}}{\mathrm{4}}}=\frac{\mathrm{4}{r}}{\mathrm{3}}=\frac{\mathrm{4}}{\mathrm{3}} \\ $$$${BK}={BF}−{KF}=\mathrm{3}−\frac{\mathrm{4}}{\mathrm{3}}=\frac{\mathrm{5}}{\mathrm{3}} \\ $$$$\frac{{CK}}{{BK}}=\frac{{CG}}{{EG}}=\frac{\mathrm{2}}{\mathrm{1}} \\ $$$$\Rightarrow{CK}=\mathrm{2}{BK}=\frac{\mathrm{10}}{\mathrm{3}} \\ $$$${BC}={BK}+{CK}=\frac{\mathrm{5}}{\mathrm{3}}+\frac{\mathrm{10}}{\mathrm{3}}=\mathrm{5} \\ $$$${FC}={BC}−{BF}=\mathrm{5}−\mathrm{3}=\mathrm{2} \\ $$$$\mathrm{tan}\:\frac{\gamma}{\mathrm{2}}=\frac{{IF}}{{FC}}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\mathrm{tan}\:\gamma=\frac{\mathrm{2}×\frac{\mathrm{1}}{\mathrm{2}}}{\mathrm{1}−\left(\frac{\mathrm{1}}{\mathrm{2}}\right)^{\mathrm{2}} }=\frac{\mathrm{4}}{\mathrm{3}}=\frac{\mathrm{1}}{\mathrm{tan}\:\beta} \\ $$$$\mathrm{tan}\:\beta×\mathrm{tan}\:\gamma=\mathrm{1} \\ $$$$\Rightarrow\beta+\gamma=\mathrm{90}° \\ $$$$\alpha=\mathrm{180}°−\beta−\gamma \\ $$$$\Rightarrow\alpha=\mathrm{90}° \\ $$
Commented by TawaTawa last updated on 24/Feb/20

$$\mathrm{Wow},\:\mathrm{God}\:\mathrm{bless}\:\mathrm{you}\:\mathrm{sir}.\:\mathrm{I}\:\mathrm{really}\:\mathrm{appreciate}\:\mathrm{your}\:\mathrm{time}. \\ $$
Commented by TawaTawa last updated on 24/Feb/20

$$\mathrm{Sir}\:\mathrm{from}\:\mathrm{the}\:\mathrm{diagram}.\:\mathrm{How}\:\mathrm{is}\:\:\mathrm{IK}\:\:=\:\:\mathrm{BE} \\ $$
Commented by mr W last updated on 24/Feb/20
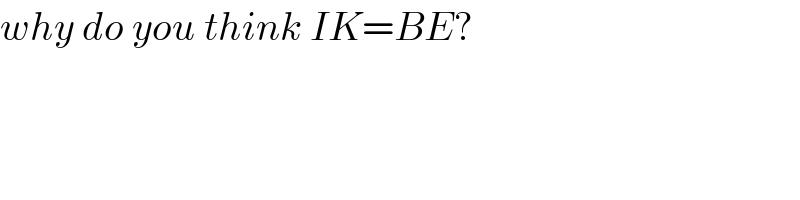
$${why}\:{do}\:{you}\:{think}\:{IK}={BE}? \\ $$
Commented by mr W last updated on 24/Feb/20
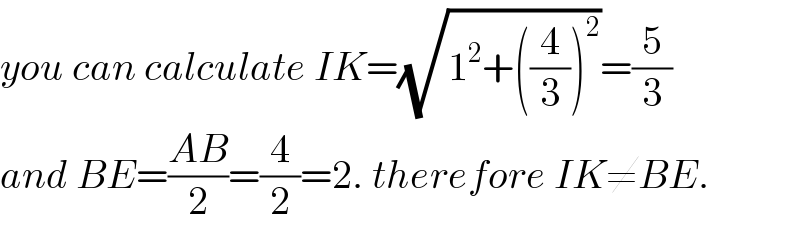
$${you}\:{can}\:{calculate}\:{IK}=\sqrt{\mathrm{1}^{\mathrm{2}} +\left(\frac{\mathrm{4}}{\mathrm{3}}\right)^{\mathrm{2}} }=\frac{\mathrm{5}}{\mathrm{3}} \\ $$$${and}\:{BE}=\frac{{AB}}{\mathrm{2}}=\frac{\mathrm{4}}{\mathrm{2}}=\mathrm{2}.\:{therefore}\:{IK}\neq{BE}. \\ $$
Commented by TawaTawa1 last updated on 24/Feb/20
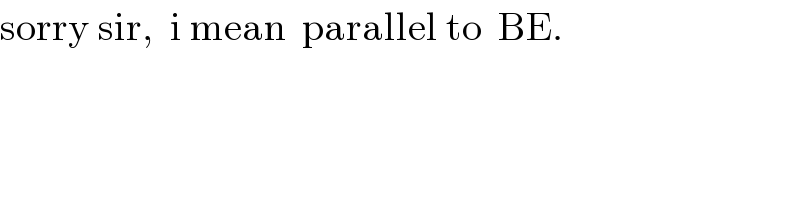
$$\mathrm{sorry}\:\mathrm{sir},\:\:\mathrm{i}\:\mathrm{mean}\:\:\mathrm{parallel}\:\mathrm{to}\:\:\mathrm{BE}. \\ $$
Commented by mr W last updated on 24/Feb/20
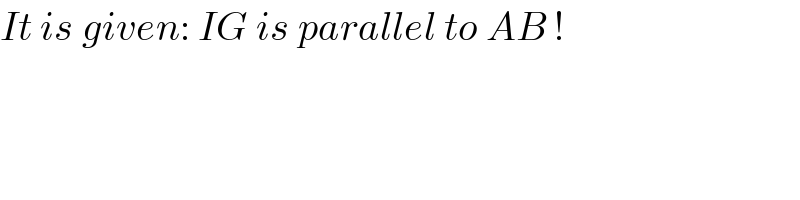
$${It}\:{is}\:{given}:\:{IG}\:{is}\:{parallel}\:{to}\:{AB}\:! \\ $$
Commented by TawaTawa1 last updated on 24/Feb/20
$$\mathrm{Oh},\:\mathrm{thank}\:\mathrm{you}\:\mathrm{sir},\:\mathrm{i}\:\mathrm{appreciate}. \\ $$
