Menu Close

Question-82806

Tinku Tara 0 Comments
Pin




Question Number 82806 by ajfour last updated on 24/Feb/20
Commented by ajfour last updated on 24/Feb/20
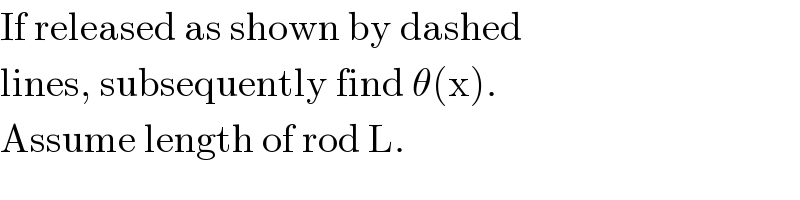
If released as shown by dashed lines, subsequently find θ(x). Assume length of rod L.
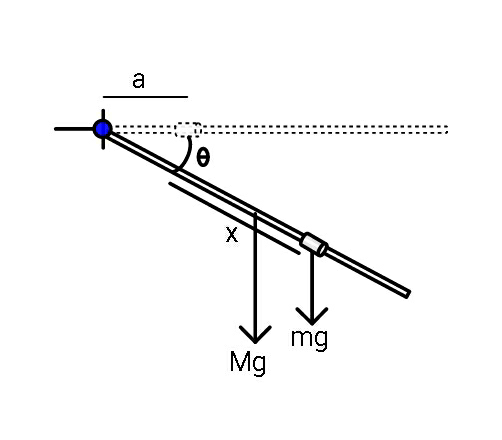
$$\mathrm{If}\:\mathrm{released}\:\mathrm{as}\:\mathrm{shown}\:\mathrm{by}\:\mathrm{dashed} \\ $$$$\mathrm{lines},\:\mathrm{subsequently}\:\mathrm{find}\:\theta\left(\mathrm{x}\right). \\ $$$$\mathrm{Assume}\:\mathrm{length}\:\mathrm{of}\:\mathrm{rod}\:\mathrm{L}. \\ $$
Answered by mr W last updated on 24/Feb/20
Commented by mr W last updated on 24/Feb/20
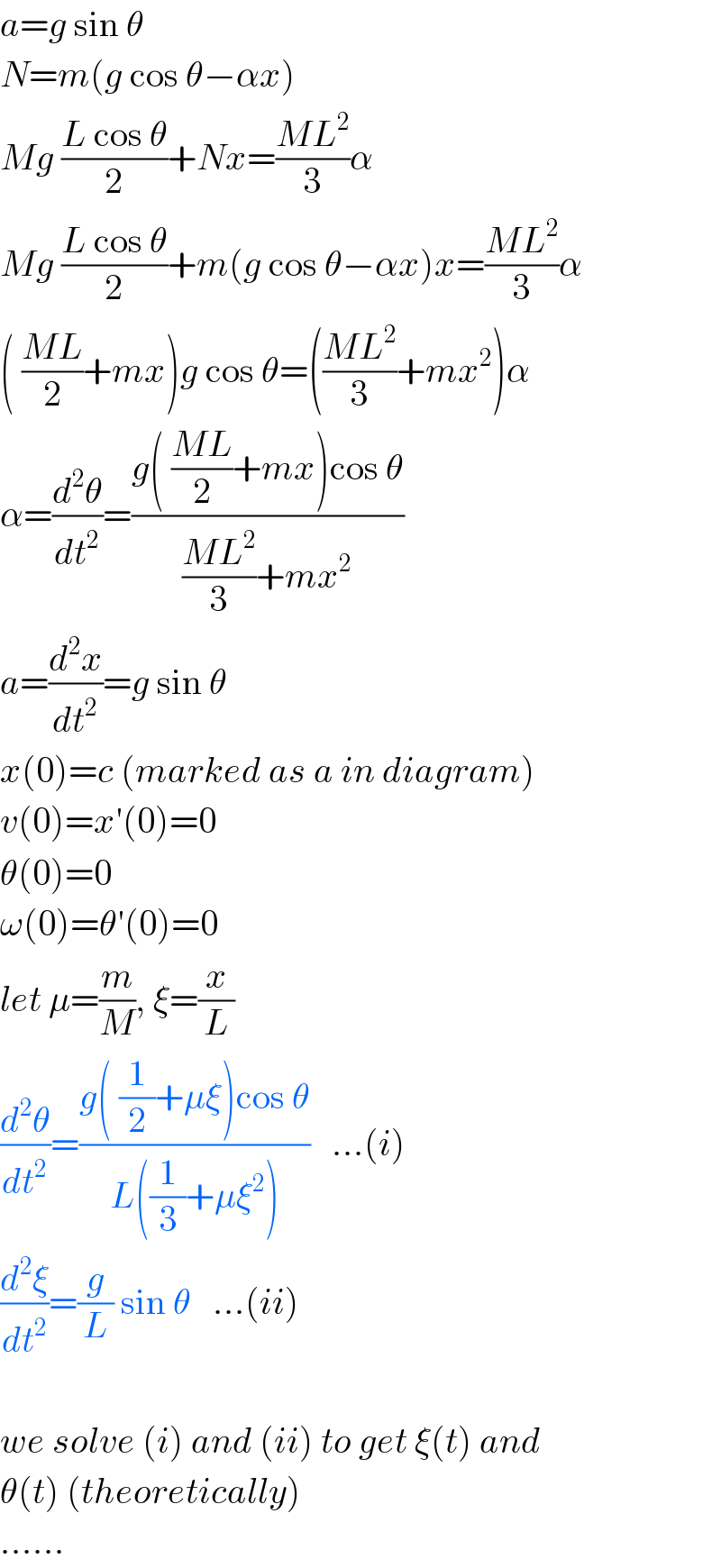
a=g sin θ N=m(g cos θ−αx) Mg ((L cos θ)/2)+Nx=((ML^2 )/3)α Mg ((L cos θ)/2)+m(g cos θ−αx)x=((ML^2 )/3)α ( ((ML)/2)+mx)g cos θ=(((ML^2 )/3)+mx^2 )α α=(d^2 θ/dt^2 )=((g( ((ML)/2)+mx)cos θ)/(((ML^2 )/3)+mx^2 )) a=(d^2 x/dt^2 )=g sin θ x(0)=c (marked as a in diagram) v(0)=x′(0)=0 θ(0)=0 ω(0)=θ′(0)=0 let μ=(m/M), ξ=(x/L) (d^2 θ/dt^2 )=((g( (1/2)+μξ)cos θ)/(L((1/3)+μξ^2 ))) ...(i) (d^2 ξ/dt^2 )=(g/L) sin θ ...(ii) we solve (i) and (ii) to get ξ(t) and θ(t) (theoretically) ......
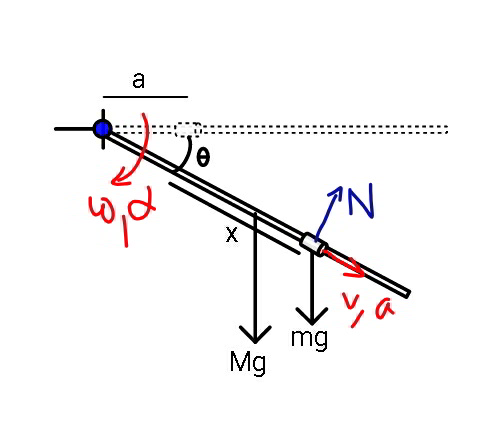
$${a}={g}\:\mathrm{sin}\:\theta \\ $$$${N}={m}\left({g}\:\mathrm{cos}\:\theta−\alpha{x}\right) \\ $$$${Mg}\:\frac{{L}\:\mathrm{cos}\:\theta}{\mathrm{2}}+{Nx}=\frac{{ML}^{\mathrm{2}} }{\mathrm{3}}\alpha \\ $$$${Mg}\:\frac{{L}\:\mathrm{cos}\:\theta}{\mathrm{2}}+{m}\left({g}\:\mathrm{cos}\:\theta−\alpha{x}\right){x}=\frac{{ML}^{\mathrm{2}} }{\mathrm{3}}\alpha \\ $$$$\left(\:\frac{{ML}}{\mathrm{2}}+{mx}\right){g}\:\mathrm{cos}\:\theta=\left(\frac{{ML}^{\mathrm{2}} }{\mathrm{3}}+{mx}^{\mathrm{2}} \right)\alpha \\ $$$$\alpha=\frac{{d}^{\mathrm{2}} \theta}{{dt}^{\mathrm{2}} }=\frac{{g}\left(\:\frac{{ML}}{\mathrm{2}}+{mx}\right)\mathrm{cos}\:\theta}{\frac{{ML}^{\mathrm{2}} }{\mathrm{3}}+{mx}^{\mathrm{2}} } \\ $$$${a}=\frac{{d}^{\mathrm{2}} {x}}{{dt}^{\mathrm{2}} }={g}\:\mathrm{sin}\:\theta \\ $$$${x}\left(\mathrm{0}\right)={c}\:\left({marked}\:{as}\:{a}\:{in}\:{diagram}\right) \\ $$$${v}\left(\mathrm{0}\right)={x}'\left(\mathrm{0}\right)=\mathrm{0} \\ $$$$\theta\left(\mathrm{0}\right)=\mathrm{0} \\ $$$$\omega\left(\mathrm{0}\right)=\theta'\left(\mathrm{0}\right)=\mathrm{0} \\ $$$${let}\:\mu=\frac{{m}}{{M}},\:\xi=\frac{{x}}{{L}} \\ $$$$\frac{{d}^{\mathrm{2}} \theta}{{dt}^{\mathrm{2}} }=\frac{{g}\left(\:\frac{\mathrm{1}}{\mathrm{2}}+\mu\xi\right)\mathrm{cos}\:\theta}{{L}\left(\frac{\mathrm{1}}{\mathrm{3}}+\mu\xi^{\mathrm{2}} \right)}\:\:\:…\left({i}\right) \\ $$$$\frac{{d}^{\mathrm{2}} \xi}{{dt}^{\mathrm{2}} }=\frac{{g}}{{L}}\:\mathrm{sin}\:\theta\:\:\:…\left({ii}\right) \\ $$$$ \\ $$$${we}\:{solve}\:\left({i}\right)\:{and}\:\left({ii}\right)\:{to}\:{get}\:\xi\left({t}\right)\:{and} \\ $$$$\theta\left({t}\right)\:\left({theoretically}\right) \\ $$$$…… \\ $$
Commented by ajfour last updated on 24/Feb/20
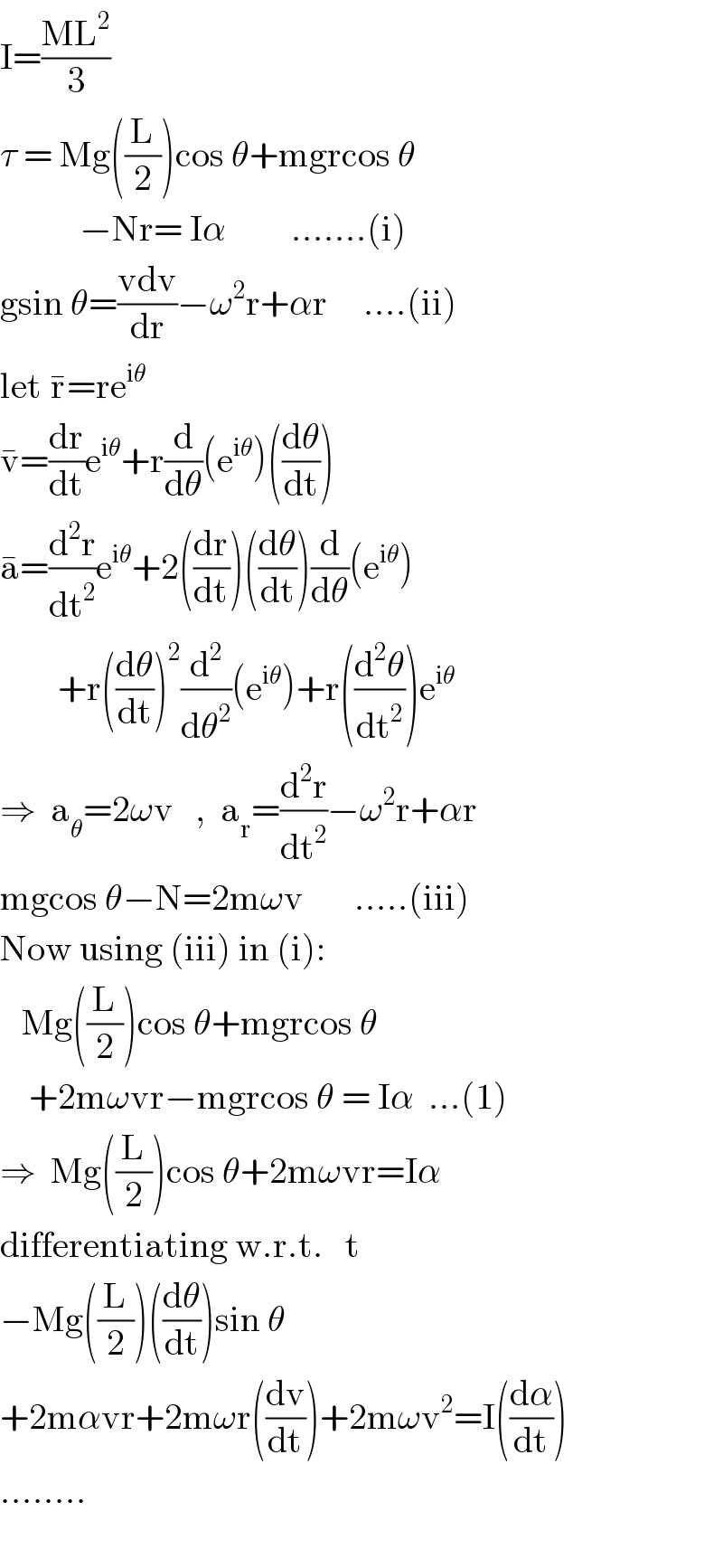
I=((ML^2 )/3) τ = Mg((L/2))cos θ+mgrcos θ −Nr= Iα .......(i) gsin θ=((vdv)/dr)−ω^2 r+αr ....(ii) let r^� =re^(iθ) v^� =(dr/dt)e^(iθ) +r(d/dθ)(e^(iθ) )((dθ/dt)) a^� =(d^2 r/dt^2 )e^(iθ) +2((dr/dt))((dθ/dt))(d/dθ)(e^(iθ) ) +r((dθ/dt))^2 (d^2 /dθ^2 )(e^(iθ) )+r((d^2 θ/dt^2 ))e^(iθ) ⇒ a_θ =2ωv , a_r =(d^2 r/dt^2 )−ω^2 r+αr mgcos θ−N=2mωv .....(iii) Now using (iii) in (i): Mg((L/2))cos θ+mgrcos θ +2mωvr−mgrcos θ = Iα ...(1) ⇒ Mg((L/2))cos θ+2mωvr=Iα differentiating w.r.t. t −Mg((L/2))((dθ/dt))sin θ +2mαvr+2mωr((dv/dt))+2mωv^2 =I((dα/dt)) ........
$$\mathrm{I}=\frac{\mathrm{ML}^{\mathrm{2}} }{\mathrm{3}} \\ $$$$\tau\:=\:\mathrm{Mg}\left(\frac{\mathrm{L}}{\mathrm{2}}\right)\mathrm{cos}\:\theta+\mathrm{mgrcos}\:\theta \\ $$$$\:\:\:\:\:\:\:\:\:\:\:−\mathrm{Nr}=\:\mathrm{I}\alpha\:\:\:\:\:\:\:\:\:…….\left(\mathrm{i}\right)\: \\ $$$$\mathrm{gsin}\:\theta=\frac{\mathrm{vdv}}{\mathrm{dr}}−\omega^{\mathrm{2}} \mathrm{r}+\alpha\mathrm{r}\:\:\:\:\:….\left(\mathrm{ii}\right) \\ $$$$\mathrm{let}\:\bar {\mathrm{r}}=\mathrm{re}^{\mathrm{i}\theta} \\ $$$$\bar {\mathrm{v}}=\frac{\mathrm{dr}}{\mathrm{dt}}\mathrm{e}^{\mathrm{i}\theta} +\mathrm{r}\frac{\mathrm{d}}{\mathrm{d}\theta}\left(\mathrm{e}^{\mathrm{i}\theta} \right)\left(\frac{\mathrm{d}\theta}{\mathrm{dt}}\right) \\ $$$$\bar {\mathrm{a}}=\frac{\mathrm{d}^{\mathrm{2}} \mathrm{r}}{\mathrm{dt}^{\mathrm{2}} }\mathrm{e}^{\mathrm{i}\theta} +\mathrm{2}\left(\frac{\mathrm{dr}}{\mathrm{dt}}\right)\left(\frac{\mathrm{d}\theta}{\mathrm{dt}}\right)\frac{\mathrm{d}}{\mathrm{d}\theta}\left(\mathrm{e}^{\mathrm{i}\theta} \right) \\ $$$$\:\:\:\:\:\:\:\:+\mathrm{r}\left(\frac{\mathrm{d}\theta}{\mathrm{dt}}\right)^{\mathrm{2}} \frac{\mathrm{d}^{\mathrm{2}} }{\mathrm{d}\theta^{\mathrm{2}} }\left(\mathrm{e}^{\mathrm{i}\theta} \right)+\mathrm{r}\left(\frac{\mathrm{d}^{\mathrm{2}} \theta}{\mathrm{dt}^{\mathrm{2}} }\right)\mathrm{e}^{\mathrm{i}\theta} \: \\ $$$$\Rightarrow\:\:\mathrm{a}_{\theta} =\mathrm{2}\omega\mathrm{v}\:\:\:,\:\:\mathrm{a}_{\mathrm{r}} =\frac{\mathrm{d}^{\mathrm{2}} \mathrm{r}}{\mathrm{dt}^{\mathrm{2}} }−\omega^{\mathrm{2}} \mathrm{r}+\alpha\mathrm{r} \\ $$$$\mathrm{mgcos}\:\theta−\mathrm{N}=\mathrm{2m}\omega\mathrm{v}\:\:\:\:\:\:\:…..\left(\mathrm{iii}\right) \\ $$$$\mathrm{Now}\:\mathrm{using}\:\left(\mathrm{iii}\right)\:\mathrm{in}\:\left(\mathrm{i}\right): \\ $$$$\:\:\:\mathrm{Mg}\left(\frac{\mathrm{L}}{\mathrm{2}}\right)\mathrm{cos}\:\theta+\mathrm{mgrcos}\:\theta \\ $$$$\:\:\:\:+\mathrm{2m}\omega\mathrm{vr}−\mathrm{mgrcos}\:\theta\:=\:\mathrm{I}\alpha\:\:…\left(\mathrm{1}\right) \\ $$$$\Rightarrow\:\:\mathrm{Mg}\left(\frac{\mathrm{L}}{\mathrm{2}}\right)\mathrm{cos}\:\theta+\mathrm{2m}\omega\mathrm{vr}=\mathrm{I}\alpha \\ $$$$\mathrm{differentiating}\:\mathrm{w}.\mathrm{r}.\mathrm{t}.\:\:\:\mathrm{t} \\ $$$$−\mathrm{Mg}\left(\frac{\mathrm{L}}{\mathrm{2}}\right)\left(\frac{\mathrm{d}\theta}{\mathrm{dt}}\right)\mathrm{sin}\:\theta \\ $$$$+\mathrm{2m}\alpha\mathrm{vr}+\mathrm{2m}\omega\mathrm{r}\left(\frac{\mathrm{dv}}{\mathrm{dt}}\right)+\mathrm{2m}\omega\mathrm{v}^{\mathrm{2}} =\mathrm{I}\left(\frac{\mathrm{d}\alpha}{\mathrm{dt}}\right) \\ $$$$…….. \\ $$$$ \\ $$
Commented by mr W last updated on 24/Feb/20
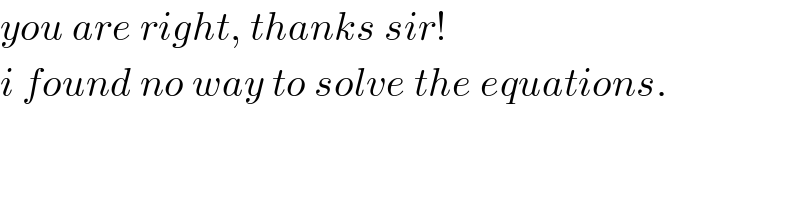
you are right, thanks sir! i found no way to solve the equations.
$${you}\:{are}\:{right},\:{thanks}\:{sir}! \\ $$$${i}\:{found}\:{no}\:{way}\:{to}\:{solve}\:{the}\:{equations}. \\ $$
Commented by ajfour last updated on 24/Feb/20
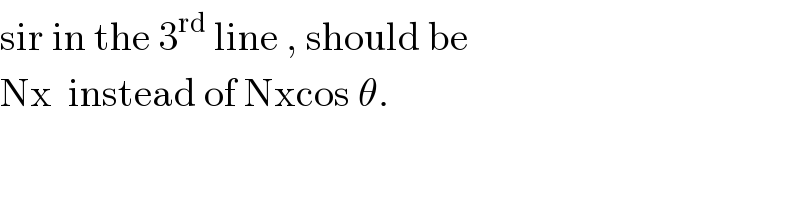
sir in the 3^(rd) line , should be Nx instead of Nxcos θ.
$$\mathrm{sir}\:\mathrm{in}\:\mathrm{the}\:\mathrm{3}^{\mathrm{rd}} \:\mathrm{line}\:,\:\mathrm{should}\:\mathrm{be}\:\: \\ $$$$\mathrm{Nx}\:\:\mathrm{instead}\:\mathrm{of}\:\mathrm{Nxcos}\:\theta. \\ $$
Commented by mr W last updated on 24/Feb/20
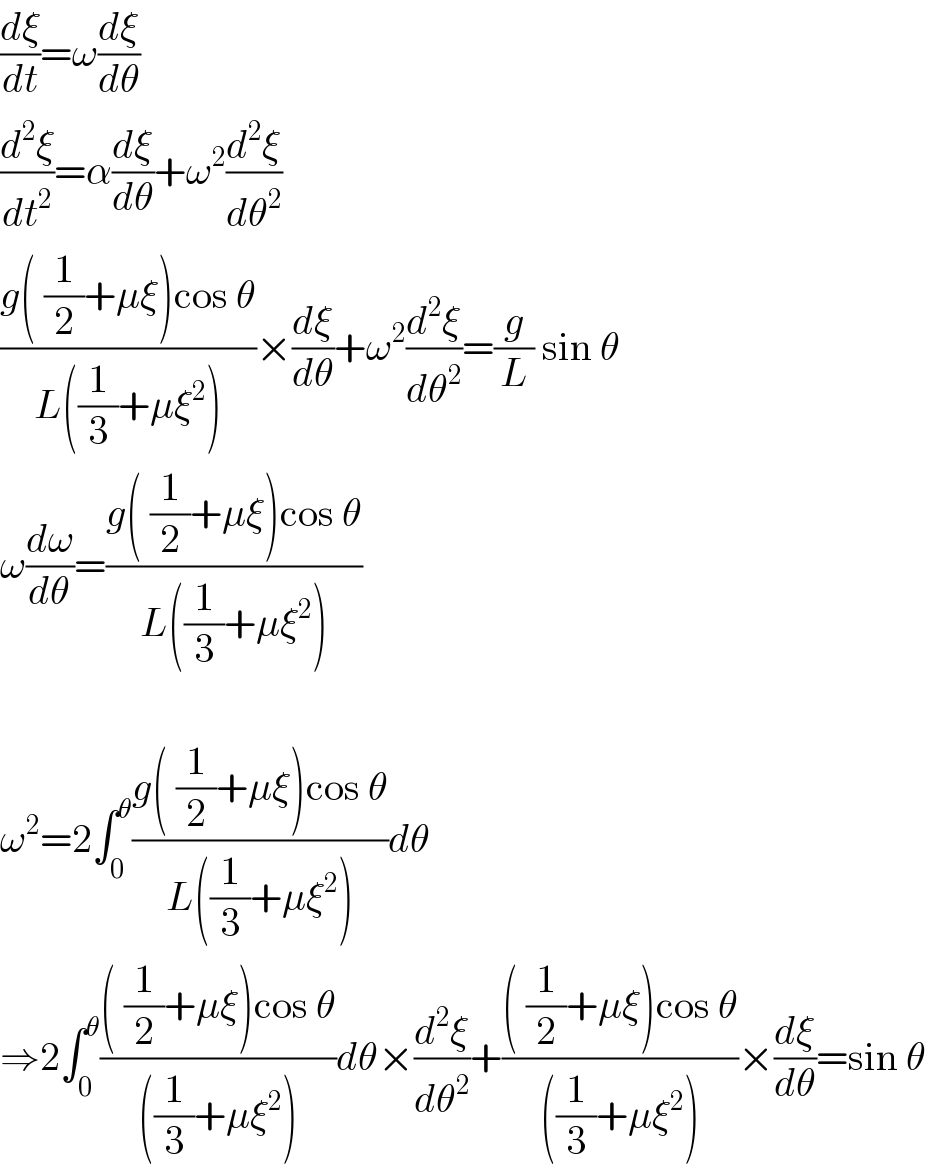
(dξ/dt)=ω(dξ/dθ) (d^2 ξ/dt^2 )=α(dξ/dθ)+ω^2 (d^2 ξ/dθ^2 ) ((g( (1/2)+μξ)cos θ)/(L((1/3)+μξ^2 )))×(dξ/dθ)+ω^2 (d^2 ξ/dθ^2 )=(g/L) sin θ ω(dω/dθ)=((g( (1/2)+μξ)cos θ)/(L((1/3)+μξ^2 ))) ω^2 =2∫_0 ^θ ((g( (1/2)+μξ)cos θ)/(L((1/3)+μξ^2 )))dθ ⇒2∫_0 ^θ ((( (1/2)+μξ)cos θ)/(((1/3)+μξ^2 )))dθ×(d^2 ξ/dθ^2 )+((( (1/2)+μξ)cos θ)/(((1/3)+μξ^2 )))×(dξ/dθ)=sin θ
$$\frac{{d}\xi}{{dt}}=\omega\frac{{d}\xi}{{d}\theta} \\ $$$$\frac{{d}^{\mathrm{2}} \xi}{{dt}^{\mathrm{2}} }=\alpha\frac{{d}\xi}{{d}\theta}+\omega^{\mathrm{2}} \frac{{d}^{\mathrm{2}} \xi}{{d}\theta^{\mathrm{2}} } \\ $$$$\frac{{g}\left(\:\frac{\mathrm{1}}{\mathrm{2}}+\mu\xi\right)\mathrm{cos}\:\theta}{{L}\left(\frac{\mathrm{1}}{\mathrm{3}}+\mu\xi^{\mathrm{2}} \right)}×\frac{{d}\xi}{{d}\theta}+\omega^{\mathrm{2}} \frac{{d}^{\mathrm{2}} \xi}{{d}\theta^{\mathrm{2}} }=\frac{{g}}{{L}}\:\mathrm{sin}\:\theta\: \\ $$$$\omega\frac{{d}\omega}{{d}\theta}=\frac{{g}\left(\:\frac{\mathrm{1}}{\mathrm{2}}+\mu\xi\right)\mathrm{cos}\:\theta}{{L}\left(\frac{\mathrm{1}}{\mathrm{3}}+\mu\xi^{\mathrm{2}} \right)} \\ $$$$ \\ $$$$\omega^{\mathrm{2}} =\mathrm{2}\int_{\mathrm{0}} ^{\theta} \frac{{g}\left(\:\frac{\mathrm{1}}{\mathrm{2}}+\mu\xi\right)\mathrm{cos}\:\theta}{{L}\left(\frac{\mathrm{1}}{\mathrm{3}}+\mu\xi^{\mathrm{2}} \right)}{d}\theta \\ $$$$\Rightarrow\mathrm{2}\int_{\mathrm{0}} ^{\theta} \frac{\left(\:\frac{\mathrm{1}}{\mathrm{2}}+\mu\xi\right)\mathrm{cos}\:\theta}{\left(\frac{\mathrm{1}}{\mathrm{3}}+\mu\xi^{\mathrm{2}} \right)}{d}\theta×\frac{{d}^{\mathrm{2}} \xi}{{d}\theta^{\mathrm{2}} }+\frac{\left(\:\frac{\mathrm{1}}{\mathrm{2}}+\mu\xi\right)\mathrm{cos}\:\theta}{\left(\frac{\mathrm{1}}{\mathrm{3}}+\mu\xi^{\mathrm{2}} \right)}×\frac{{d}\xi}{{d}\theta}=\mathrm{sin}\:\theta\: \\ $$
Commented by ajfour last updated on 24/Feb/20
Thanks sir, bringing it as far, but let us rather focus on something smoother..
$$\mathrm{Thanks}\:\mathrm{sir},\:\mathrm{bringing}\:\mathrm{it}\:\mathrm{as}\:\mathrm{far},\:\mathrm{but} \\ $$$$\mathrm{let}\:\mathrm{us}\:\mathrm{rather}\:\mathrm{focus}\:\mathrm{on}\:\mathrm{something} \\ $$$$\mathrm{smoother}.. \\ $$
Commented by mr W last updated on 24/Feb/20
yes sir! what′s about Q81968? can you post your solution sir?
$${yes}\:{sir}! \\ $$$${what}'{s}\:{about}\:{Q}\mathrm{81968}?\:{can}\:{you}\:{post} \\ $$$${your}\:{solution}\:{sir}? \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *