Question Number 82873 by mr W last updated on 25/Feb/20
Commented by mr W last updated on 25/Feb/20

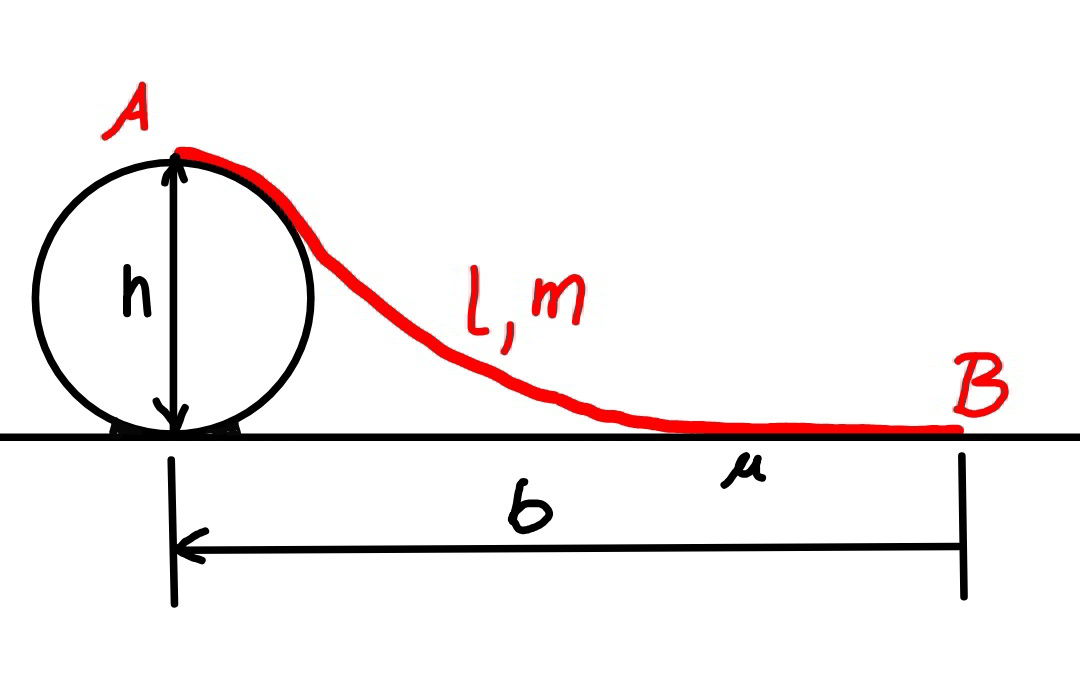
$${A}\:{rope}\:{with}\:{length}\:\boldsymbol{{l}}\:{and}\:{mass}\:\boldsymbol{{m}}\:{is} \\ $$$${fixed}\:{at}\:{one}\:{end}\:{on}\:{the}\:{top}\:{of}\:{a}\:{roller} \\ $$$${with}\:{diameter}\:{h}\:{as}\:{shown}.\:{Find}\:{the} \\ $$$${maximal}\:{possible}\:{horizontal}\:{distance} \\ $$$$\boldsymbol{{b}}\:{from}\:{the}\:{free}\:{end}\:{to}\:{the}\:{fixed}\:{end}, \\ $$$${if}\:{the}\:{friction}\:{coefficient}\:{between} \\ $$$${the}\:{rope}\:{and}\:{the}\:{ground}\:{is}\:\boldsymbol{\mu}. \\ $$
Commented by jagoll last updated on 25/Feb/20

$$\mathrm{waw}\:\mathrm{phisic} \\ $$
Answered by mr W last updated on 25/Feb/20

Commented by mr W last updated on 27/Feb/20
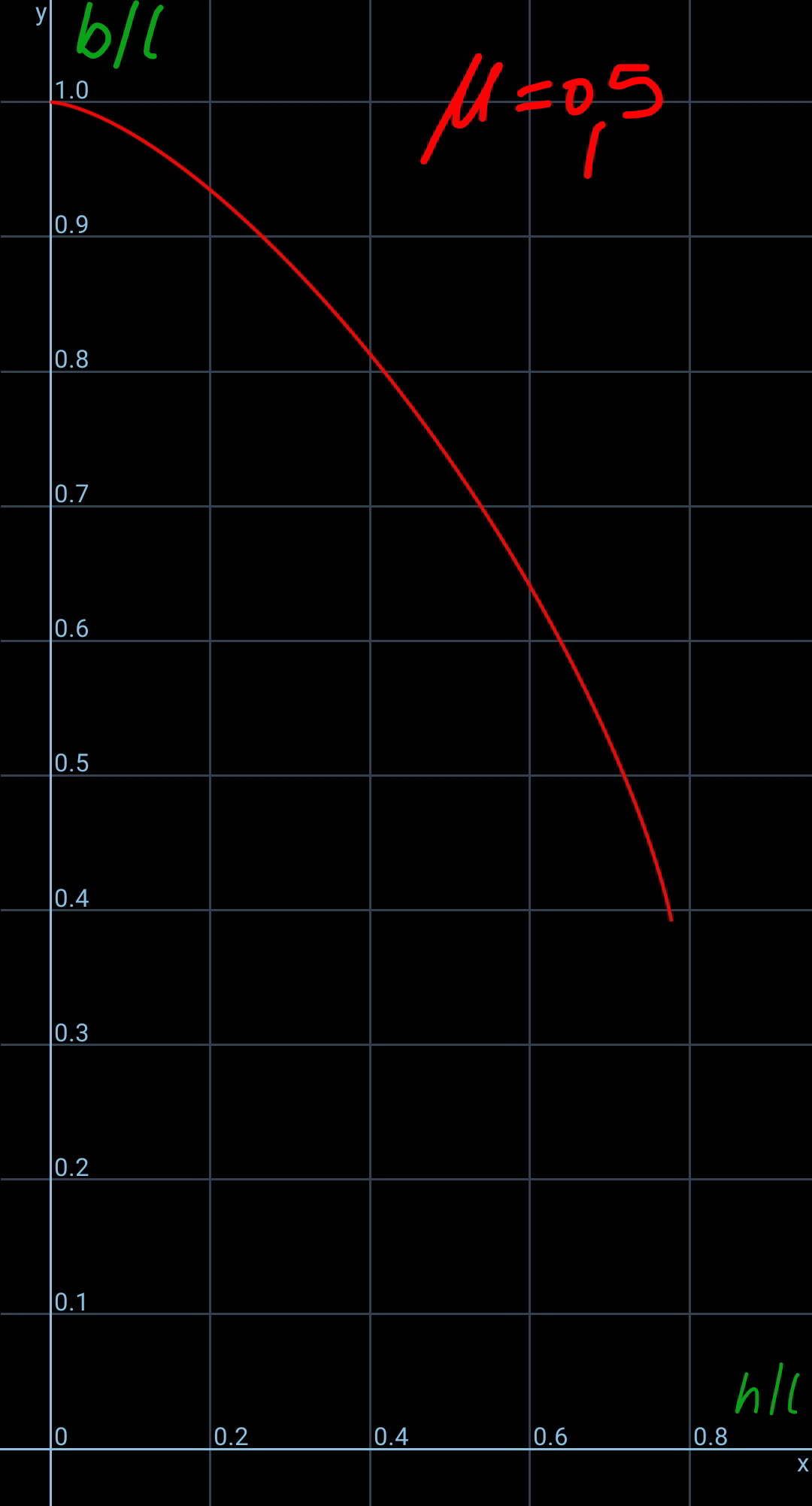
![let ρ=(m/l) the free end B is right most when the max. friction between rope and ground is activated. tension in rope at poind D is T_0 with T_0 =μρdg let a=(T_0 /(ρg))=μd the rope is divided into 3 parts: arc AC=((hθ)/2) free hanging segment CD=s segment on ground DB=d l=((hθ)/2)+s+d ⇒s=l−((hθ)/2)−d in the xy−coordinate system the shape of the hanging segment is a catenary with equation y=a cosh (x/a) y′=sinh (x/a) at point C: x_C =c=b−d−((h sin θ)/2) ...(i) y_C =a+(h/2)(1+cos θ)=a cosh (c/a) ...(ii) y_D ′=tan θ=sinh (c/a) ...(iii) s=l−d−((hθ)/2)=a sinh (c/a) ...(iv) from (iii) and (iv): l−d−((hθ)/2)=μd tan θ ⇒d=((2l−hθ)/(2(1+μ tan θ))) (ii)^2 −(iii×a)^2 : a^2 +ah(1+cos θ)+((h^2 (1+cos θ)^2 )/4)−a^2 tan^2 θ=a^2 tan^2 θ a^2 −h(1+cos θ)a−((h^2 (1+cos θ)^2 )/4)=0 ⇒a=μd=((h cos θ (1+cos θ))/(2(1−cos θ))) ⇒((μ(2l−hθ))/(cos θ+μ sin θ))=((h(1+cos θ))/(1−cos θ)) let η=(l/h) ⇒((μ(2η−θ))/(cos θ+μ sin θ))=((1+cos θ)/(1−cos θ)) ...(I) from(iii): c=a sinh^(−1) (tan θ)=μd sinh^(−1) (tan θ) from (i): b=c+d+((h sin θ)/2) b=((h cos θ (1+cos θ)[1+μ sinh^(−1) (tan θ)])/(2μ(1−cos θ)))+((h sin θ)/2) ⇒((2b)/h)=((cos θ (1+cos θ)[1+μ sinh^(−1) (tan θ)])/(μ(1−cos θ)))+sin θ ...(II) we get θ from (I) and then b from (II). example: l=10m,h=2m, η=(l/h)=((10)/2)=5, μ=0.5 ⇒θ≈0.8840 (50.65°) ⇒((2b)/h)≈9.3479 ⇒b≈9.3479 m (h/l)=(2/(θ+(((1+cos θ)(cos θ+μ sin θ))/(μ(1−cos θ))))) (b/l)=(h/(2l)){((cos θ (1+cos θ)[1+μ sinh^(−1) (tan θ)])/(μ(1−cos θ)))+sin θ} using θ as parameter we can get the relation between (b/l) and (h/l), see diagram.](https://www.tinkutara.com/question/Q82913.png)
$${let}\:\rho=\frac{{m}}{{l}} \\ $$$${the}\:{free}\:{end}\:{B}\:{is}\:{right}\:{most}\:{when} \\ $$$${the}\:{max}.\:{friction}\:{between}\:{rope}\:{and} \\ $$$${ground}\:{is}\:{activated}. \\ $$$$ \\ $$$${tension}\:{in}\:{rope}\:{at}\:{poind}\:{D}\:{is}\:{T}_{\mathrm{0}} \:{with} \\ $$$${T}_{\mathrm{0}} =\mu\rho{dg} \\ $$$${let}\:{a}=\frac{{T}_{\mathrm{0}} }{\rho{g}}=\mu{d} \\ $$$$ \\ $$$${the}\:{rope}\:{is}\:{divided}\:{into}\:\mathrm{3}\:{parts}: \\ $$$${arc}\:{AC}=\frac{{h}\theta}{\mathrm{2}} \\ $$$${free}\:{hanging}\:{segment}\:{CD}={s} \\ $$$${segment}\:{on}\:{ground}\:{DB}={d} \\ $$$${l}=\frac{{h}\theta}{\mathrm{2}}+{s}+{d}\:\Rightarrow{s}={l}−\frac{{h}\theta}{\mathrm{2}}−{d} \\ $$$$ \\ $$$${in}\:{the}\:{xy}−{coordinate}\:{system}\:{the} \\ $$$${shape}\:{of}\:{the}\:{hanging}\:{segment}\:{is}\:{a} \\ $$$${catenary}\:{with}\:{equation} \\ $$$${y}={a}\:\mathrm{cosh}\:\frac{{x}}{{a}} \\ $$$${y}'=\mathrm{sinh}\:\frac{{x}}{{a}} \\ $$$$ \\ $$$${at}\:{point}\:{C}: \\ $$$${x}_{{C}} ={c}={b}−{d}−\frac{{h}\:\mathrm{sin}\:\theta}{\mathrm{2}}\:\:\:…\left({i}\right) \\ $$$${y}_{{C}} ={a}+\frac{{h}}{\mathrm{2}}\left(\mathrm{1}+\mathrm{cos}\:\theta\right)={a}\:\mathrm{cosh}\:\frac{{c}}{{a}}\:\:\:…\left({ii}\right) \\ $$$${y}_{{D}} '=\mathrm{tan}\:\theta=\mathrm{sinh}\:\frac{{c}}{{a}}\:\:\:…\left({iii}\right) \\ $$$${s}={l}−{d}−\frac{{h}\theta}{\mathrm{2}}={a}\:\mathrm{sinh}\:\frac{{c}}{{a}}\:\:\:…\left({iv}\right) \\ $$$${from}\:\left({iii}\right)\:{and}\:\left({iv}\right): \\ $$$${l}−{d}−\frac{{h}\theta}{\mathrm{2}}=\mu{d}\:\mathrm{tan}\:\theta \\ $$$$\Rightarrow{d}=\frac{\mathrm{2}{l}−{h}\theta}{\mathrm{2}\left(\mathrm{1}+\mu\:\mathrm{tan}\:\theta\right)} \\ $$$$\left({ii}\right)^{\mathrm{2}} −\left({iii}×{a}\right)^{\mathrm{2}} : \\ $$$${a}^{\mathrm{2}} +{ah}\left(\mathrm{1}+\mathrm{cos}\:\theta\right)+\frac{{h}^{\mathrm{2}} \left(\mathrm{1}+\mathrm{cos}\:\theta\right)^{\mathrm{2}} }{\mathrm{4}}−{a}^{\mathrm{2}} \mathrm{tan}^{\mathrm{2}} \:\theta={a}^{\mathrm{2}} \\ $$$$\mathrm{tan}^{\mathrm{2}} \:\theta\:{a}^{\mathrm{2}} −{h}\left(\mathrm{1}+\mathrm{cos}\:\theta\right){a}−\frac{{h}^{\mathrm{2}} \left(\mathrm{1}+\mathrm{cos}\:\theta\right)^{\mathrm{2}} }{\mathrm{4}}=\mathrm{0} \\ $$$$\Rightarrow{a}=\mu{d}=\frac{{h}\:\mathrm{cos}\:\theta\:\left(\mathrm{1}+\mathrm{cos}\:\theta\right)}{\mathrm{2}\left(\mathrm{1}−\mathrm{cos}\:\theta\right)} \\ $$$$\Rightarrow\frac{\mu\left(\mathrm{2}{l}−{h}\theta\right)}{\mathrm{cos}\:\theta+\mu\:\mathrm{sin}\:\theta}=\frac{{h}\left(\mathrm{1}+\mathrm{cos}\:\theta\right)}{\mathrm{1}−\mathrm{cos}\:\theta} \\ $$$${let}\:\eta=\frac{{l}}{{h}} \\ $$$$\Rightarrow\frac{\mu\left(\mathrm{2}\eta−\theta\right)}{\mathrm{cos}\:\theta+\mu\:\mathrm{sin}\:\theta}=\frac{\mathrm{1}+\mathrm{cos}\:\theta}{\mathrm{1}−\mathrm{cos}\:\theta}\:\:\:\:…\left({I}\right) \\ $$$$ \\ $$$${from}\left({iii}\right): \\ $$$${c}={a}\:\mathrm{sinh}^{−\mathrm{1}} \:\left(\mathrm{tan}\:\theta\right)=\mu{d}\:\:\mathrm{sinh}^{−\mathrm{1}} \:\left(\mathrm{tan}\:\theta\right) \\ $$$${from}\:\left({i}\right): \\ $$$${b}={c}+{d}+\frac{{h}\:\mathrm{sin}\:\theta}{\mathrm{2}} \\ $$$${b}=\frac{{h}\:\mathrm{cos}\:\theta\:\left(\mathrm{1}+\mathrm{cos}\:\theta\right)\left[\mathrm{1}+\mu\:\mathrm{sinh}^{−\mathrm{1}} \:\left(\mathrm{tan}\:\theta\right)\right]}{\mathrm{2}\mu\left(\mathrm{1}−\mathrm{cos}\:\theta\right)}+\frac{{h}\:\mathrm{sin}\:\theta}{\mathrm{2}} \\ $$$$\Rightarrow\frac{\mathrm{2}{b}}{{h}}=\frac{\mathrm{cos}\:\theta\:\left(\mathrm{1}+\mathrm{cos}\:\theta\right)\left[\mathrm{1}+\mu\:\mathrm{sinh}^{−\mathrm{1}} \:\left(\mathrm{tan}\:\theta\right)\right]}{\mu\left(\mathrm{1}−\mathrm{cos}\:\theta\right)}+\mathrm{sin}\:\theta\:\:\:…\left({II}\right) \\ $$$${we}\:{get}\:\theta\:{from}\:\left({I}\right)\:{and}\:{then}\:{b}\:{from}\:\left({II}\right).\: \\ $$$$ \\ $$$${example}: \\ $$$${l}=\mathrm{10}{m},{h}=\mathrm{2}{m},\:\eta=\frac{{l}}{{h}}=\frac{\mathrm{10}}{\mathrm{2}}=\mathrm{5},\:\mu=\mathrm{0}.\mathrm{5} \\ $$$$\Rightarrow\theta\approx\mathrm{0}.\mathrm{8840}\:\left(\mathrm{50}.\mathrm{65}°\right) \\ $$$$\Rightarrow\frac{\mathrm{2}{b}}{{h}}\approx\mathrm{9}.\mathrm{3479}\:\Rightarrow{b}\approx\mathrm{9}.\mathrm{3479}\:{m} \\ $$$$ \\ $$$$\frac{{h}}{{l}}=\frac{\mathrm{2}}{\theta+\frac{\left(\mathrm{1}+\mathrm{cos}\:\theta\right)\left(\mathrm{cos}\:\theta+\mu\:\mathrm{sin}\:\theta\right)}{\mu\left(\mathrm{1}−\mathrm{cos}\:\theta\right)}}\: \\ $$$$\frac{{b}}{{l}}=\frac{{h}}{\mathrm{2}{l}}\left\{\frac{\mathrm{cos}\:\theta\:\left(\mathrm{1}+\mathrm{cos}\:\theta\right)\left[\mathrm{1}+\mu\:\mathrm{sinh}^{−\mathrm{1}} \:\left(\mathrm{tan}\:\theta\right)\right]}{\mu\left(\mathrm{1}−\mathrm{cos}\:\theta\right)}+\mathrm{sin}\:\theta\right\} \\ $$$${using}\:\theta\:{as}\:{parameter}\:{we}\:{can}\:{get}\:{the} \\ $$$${relation}\:{between}\:\frac{{b}}{{l}}\:{and}\:\frac{{h}}{{l}},\:{see}\: \\ $$$${diagram}. \\ $$
Commented by mr W last updated on 26/Feb/20