Menu Close

Question-82897

Tinku Tara 0 Comments
Pin




Question Number 82897 by aseer imad last updated on 25/Feb/20
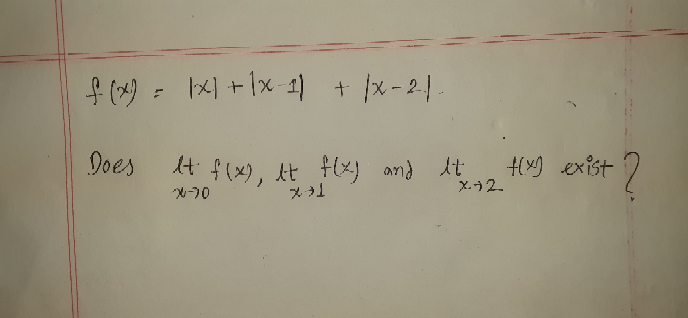
Commented by mr W last updated on 25/Feb/20
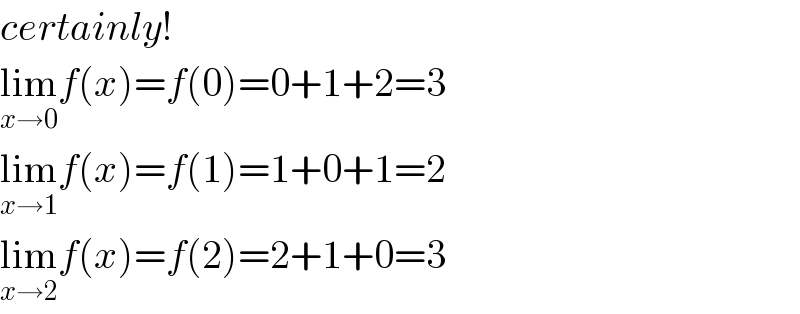
certainly! lim_(x→0) f(x)=f(0)=0+1+2=3 lim_(x→1) f(x)=f(1)=1+0+1=2 lim_(x→2) f(x)=f(2)=2+1+0=3
$${certainly}! \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}{f}\left({x}\right)={f}\left(\mathrm{0}\right)=\mathrm{0}+\mathrm{1}+\mathrm{2}=\mathrm{3} \\ $$$$\underset{{x}\rightarrow\mathrm{1}} {\mathrm{lim}}{f}\left({x}\right)={f}\left(\mathrm{1}\right)=\mathrm{1}+\mathrm{0}+\mathrm{1}=\mathrm{2} \\ $$$$\underset{{x}\rightarrow\mathrm{2}} {\mathrm{lim}}{f}\left({x}\right)={f}\left(\mathrm{2}\right)=\mathrm{2}+\mathrm{1}+\mathrm{0}=\mathrm{3} \\ $$
Commented by aseer imad last updated on 25/Feb/20
thank you
Answered by TANMAY PANACEA last updated on 25/Feb/20
critical value of x=0,1,2 f(x)=x+x−1+x−2 when x>2 =3x−3 =x+x−1−(x−2) when 2>x>1 =x+1 =x−(x−1)−(x−2) when 1>x>0 =−x+3 =−(x)−(x−1)−(x−2) when x<0 =−3x+3 now lim_(x→0+) f(x) lim_(x→0+) −x+3=3 lim_(x→0−) f(x) =lim_(x→0−) −3x+3=3 so limit exist at x=0 lim_(x→1+) f(x) lim_(x→1+) x+1=2 lim_(x→1−) −x+3=−1+3=2 limit exist at x=1 lim_(x→2−) x+1=3 lim_(x→2+) 3x−3=3 so limit exist at x=1,2 and 3 pls check...
$${critical}\:{value}\:{of}\:{x}=\mathrm{0},\mathrm{1},\mathrm{2} \\ $$$${f}\left({x}\right)={x}+{x}−\mathrm{1}+{x}−\mathrm{2}\:\:\:{when}\:{x}>\mathrm{2} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:=\mathrm{3}{x}−\mathrm{3} \\ $$$$\:\:\:\:\:\:\:\:\:\:={x}+{x}−\mathrm{1}−\left({x}−\mathrm{2}\right)\:\:\:\:{when}\:\mathrm{2}>{x}>\mathrm{1} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:={x}+\mathrm{1} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:={x}−\left({x}−\mathrm{1}\right)−\left({x}−\mathrm{2}\right)\:\:\:\:\:{when}\:\mathrm{1}>{x}>\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:=−{x}+\mathrm{3} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:=−\left({x}\right)−\left({x}−\mathrm{1}\right)−\left({x}−\mathrm{2}\right)\:\:{when}\:{x}<\mathrm{0} \\ $$$$\:\:\:\:\:\:\:\:\:\:=−\mathrm{3}{x}+\mathrm{3} \\ $$$$\boldsymbol{{now}} \\ $$$$\underset{{x}\rightarrow\mathrm{0}+} {\mathrm{lim}}\:\boldsymbol{{f}}\left(\boldsymbol{{x}}\right) \\ $$$$\underset{{x}\rightarrow\mathrm{0}+} {\mathrm{lim}}\:−\boldsymbol{{x}}+\mathrm{3}=\mathrm{3} \\ $$$$\underset{{x}\rightarrow\mathrm{0}−} {\mathrm{lim}}\:\boldsymbol{{f}}\left(\boldsymbol{{x}}\right) \\ $$$$=\underset{{x}\rightarrow\mathrm{0}−} {\mathrm{lim}}\:−\mathrm{3}\boldsymbol{{x}}+\mathrm{3}=\mathrm{3} \\ $$$$\boldsymbol{{so}}\:\boldsymbol{{limit}}\:\boldsymbol{{exist}}\:\boldsymbol{{at}}\:\boldsymbol{{x}}=\mathrm{0} \\ $$$$\underset{{x}\rightarrow\mathrm{1}+} {\mathrm{lim}}\boldsymbol{{f}}\left(\boldsymbol{{x}}\right) \\ $$$$\underset{{x}\rightarrow\mathrm{1}+} {\mathrm{lim}}\:\boldsymbol{{x}}+\mathrm{1}=\mathrm{2} \\ $$$$\underset{{x}\rightarrow\mathrm{1}−} {\mathrm{lim}}\:−\boldsymbol{{x}}+\mathrm{3}=−\mathrm{1}+\mathrm{3}=\mathrm{2} \\ $$$$\boldsymbol{{limit}}\:\boldsymbol{{exist}}\:\boldsymbol{{at}}\:\boldsymbol{{x}}=\mathrm{1} \\ $$$$\underset{{x}\rightarrow\mathrm{2}−} {\mathrm{lim}}\:\boldsymbol{{x}}+\mathrm{1}=\mathrm{3} \\ $$$$\underset{{x}\rightarrow\mathrm{2}+} {\mathrm{lim}}\:\mathrm{3}\boldsymbol{{x}}−\mathrm{3}=\mathrm{3} \\ $$$${so}\:{limit}\:{exist}\:{at}\:{x}=\mathrm{1},\mathrm{2}\:{and}\:\mathrm{3} \\ $$$${pls}\:{check}… \\ $$$$ \\ $$$$ \\ $$$$ \\ $$

Pin

Leave a Reply

Your email address will not be published. Required fields are marked *