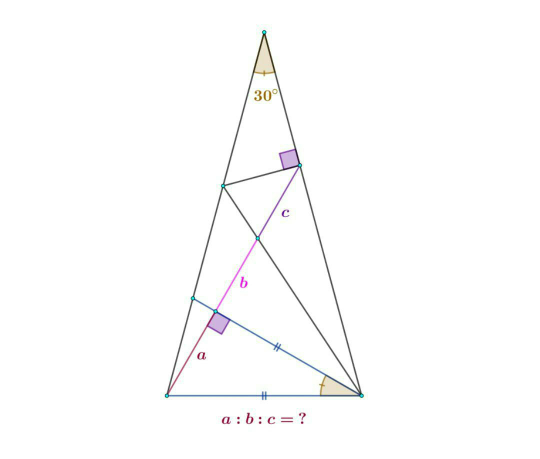
Question Number 82901 by Power last updated on 25/Feb/20
Answered by mr W last updated on 26/Feb/20
Commented by Power last updated on 26/Feb/20

$$\mathrm{sir}\:\:\mathrm{a}:\mathrm{b}:\mathrm{c}=? \\ $$
Commented by mr W last updated on 26/Feb/20
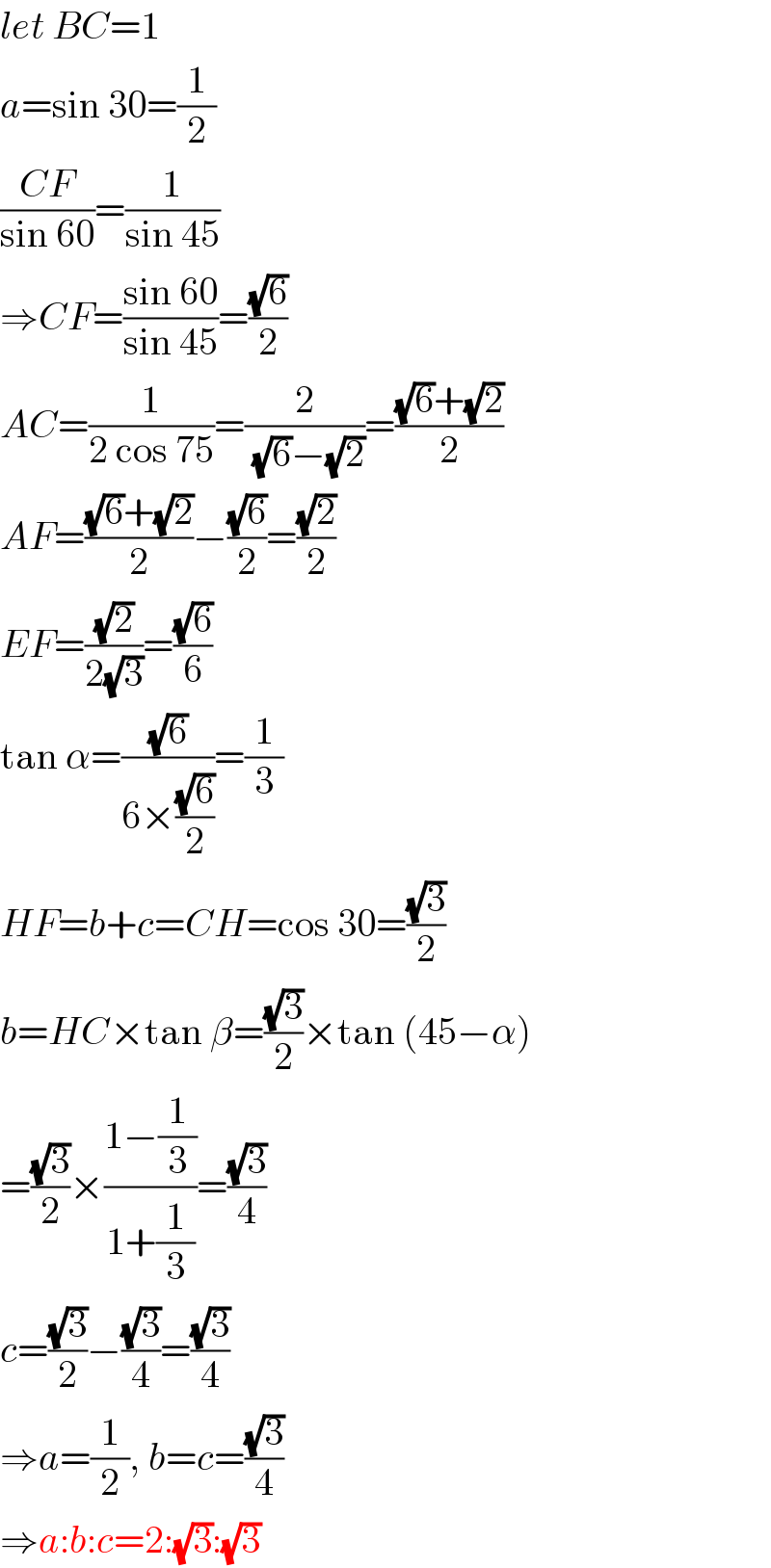
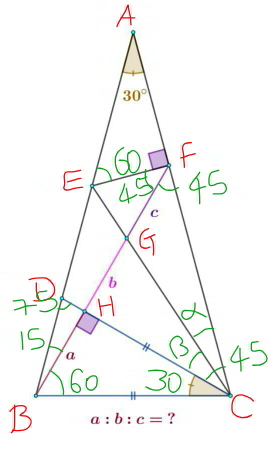
$${let}\:{BC}=\mathrm{1} \\ $$$${a}=\mathrm{sin}\:\mathrm{30}=\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\frac{{CF}}{\mathrm{sin}\:\mathrm{60}}=\frac{\mathrm{1}}{\mathrm{sin}\:\mathrm{45}} \\ $$$$\Rightarrow{CF}=\frac{\mathrm{sin}\:\mathrm{60}}{\mathrm{sin}\:\mathrm{45}}=\frac{\sqrt{\mathrm{6}}}{\mathrm{2}} \\ $$$${AC}=\frac{\mathrm{1}}{\mathrm{2}\:\mathrm{cos}\:\mathrm{75}}=\frac{\mathrm{2}}{\:\sqrt{\mathrm{6}}−\sqrt{\mathrm{2}}}=\frac{\sqrt{\mathrm{6}}+\sqrt{\mathrm{2}}}{\mathrm{2}} \\ $$$${AF}=\frac{\sqrt{\mathrm{6}}+\sqrt{\mathrm{2}}}{\mathrm{2}}−\frac{\sqrt{\mathrm{6}}}{\mathrm{2}}=\frac{\sqrt{\mathrm{2}}}{\mathrm{2}} \\ $$$${EF}=\frac{\sqrt{\mathrm{2}}}{\mathrm{2}\sqrt{\mathrm{3}}}=\frac{\sqrt{\mathrm{6}}}{\mathrm{6}} \\ $$$$\mathrm{tan}\:\alpha=\frac{\sqrt{\mathrm{6}}}{\mathrm{6}×\frac{\sqrt{\mathrm{6}}}{\mathrm{2}}}=\frac{\mathrm{1}}{\mathrm{3}} \\ $$$${HF}={b}+{c}={CH}=\mathrm{cos}\:\mathrm{30}=\frac{\sqrt{\mathrm{3}}}{\mathrm{2}} \\ $$$${b}={HC}×\mathrm{tan}\:\beta=\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}×\mathrm{tan}\:\left(\mathrm{45}−\alpha\right) \\ $$$$=\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}×\frac{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{3}}}{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{3}}}=\frac{\sqrt{\mathrm{3}}}{\mathrm{4}} \\ $$$${c}=\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}−\frac{\sqrt{\mathrm{3}}}{\mathrm{4}}=\frac{\sqrt{\mathrm{3}}}{\mathrm{4}} \\ $$$$\Rightarrow{a}=\frac{\mathrm{1}}{\mathrm{2}},\:{b}={c}=\frac{\sqrt{\mathrm{3}}}{\mathrm{4}} \\ $$$$\Rightarrow{a}:{b}:{c}=\mathrm{2}:\sqrt{\mathrm{3}}:\sqrt{\mathrm{3}} \\ $$
Commented by Power last updated on 26/Feb/20

$$\mathrm{thanks} \\ $$
