Question Number 83264 by peter frank last updated on 29/Feb/20

Commented by peter frank last updated on 29/Feb/20

$$\mathrm{7},\mathrm{12},\mathrm{13} \\ $$
Commented by mr W last updated on 29/Feb/20
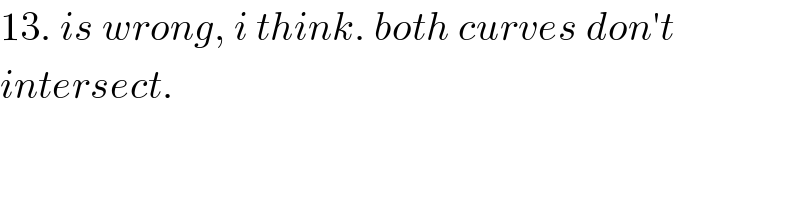
$$\mathrm{13}.\:{is}\:{wrong},\:{i}\:{think}.\:{both}\:{curves}\:{don}'{t} \\ $$$${intersect}. \\ $$
Answered by Rio Michael last updated on 29/Feb/20

$$\mathrm{7}.\:{x}^{\mathrm{2}} \:+\:{y}^{\mathrm{2}} \:=\:\mathrm{2}{x}\:\mathrm{and}\:{y}^{\mathrm{2}} \:=\:{x} \\ $$$$\:\Rightarrow\:{x}^{\mathrm{2}} \:+\:{x}\:−\mathrm{2}{x}\:=\:\mathrm{0}\:{and}\:{x}^{\mathrm{2}} −{x}\:=\:\mathrm{0}\:\Leftrightarrow\:{x}\:=\:\mathrm{0}\:\vee\:{x}\:=\:\mathrm{1} \\ $$$$\:{y}\:=\:\mathrm{0}\:{or}\:{y}\:=\:\pm\:\mathrm{1} \\ $$$${the}\:{points}\:{of}\:{intersection}\:{are}\:\:\left(\mathrm{0},\mathrm{0}\right)\:{and}\:\left(\mathrm{1},\pm\mathrm{1}\right) \\ $$$${gradient}\:{of}\:{curve}\:\mathrm{1}:\:\:\mathrm{2}{x}\:+\:\mathrm{2}{y}\:\frac{{dy}}{{dx}}\:=\:\mathrm{2}\:\Rightarrow\:\frac{{dy}}{{dx}}\:=\:\frac{\mathrm{1}−{x}}{{y}} \\ $$$${gradient}\:{of}\:{curve}\:\mathrm{2}:\:\mathrm{2}{y}\frac{{dy}}{{dx}}\:=\:\mathrm{1}\:\Rightarrow\:\frac{{dy}}{{dx}}\:=\:\frac{\mathrm{1}}{\mathrm{2}{y}} \\ $$$$\left({m}_{\mathrm{1}} ,{m}_{\mathrm{2}} \right)\:{at}\:{point}\:{of}\:{interesections}\:{are}\::\:\:\left(\mathrm{0},\:\frac{\mathrm{1}}{\mathrm{2}}\right) \\ $$$${so}\:\left(\theta_{\mathrm{1}} ,\theta_{\mathrm{2}} \right)\:=\:\left({arctan}\:\mathrm{0},\:{arctan}\:\frac{\mathrm{1}}{\mathrm{2}}\right) \\ $$$${so}\:{angle}\:{of}\:{intersection}\:\mathrm{0}°\:{and}\:{arctan}\frac{\mathrm{1}}{\mathrm{2}} \\ $$
