Question-83268

Question Number 83268 by M±th+et£s last updated on 29/Feb/20

Answered by mr W last updated on 29/Feb/20

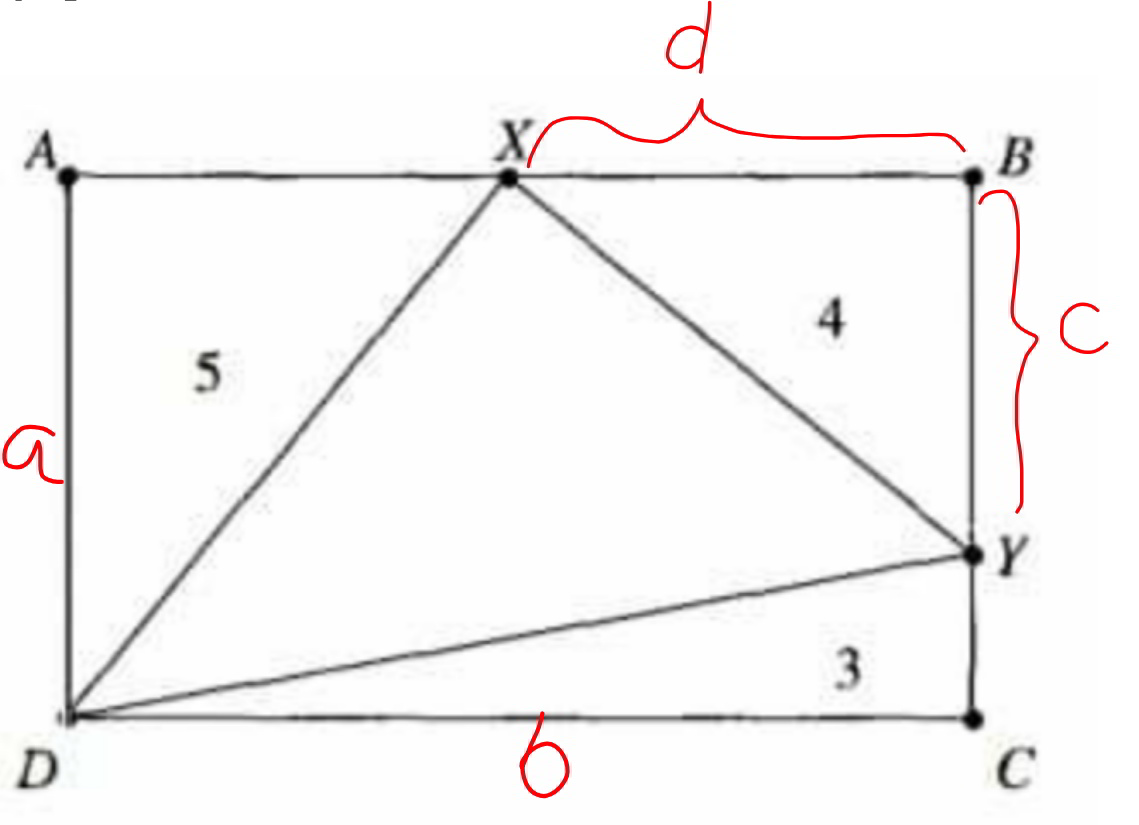
Commented by mr W last updated on 29/Feb/20

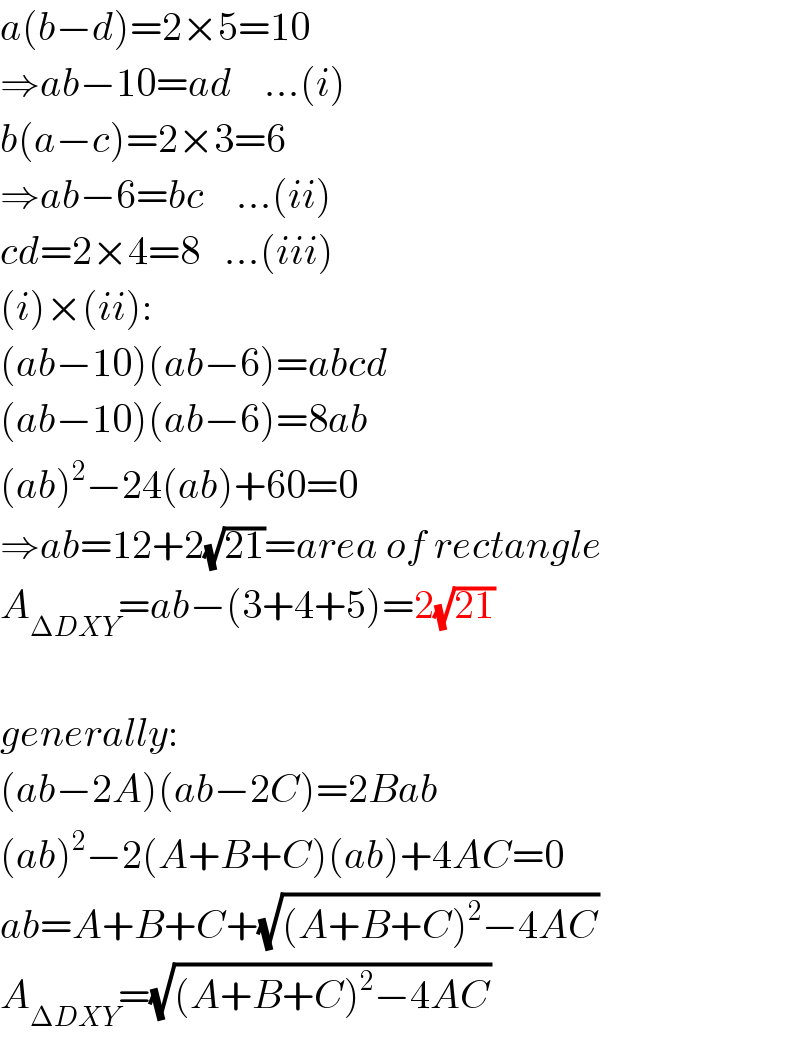
a(b−d)=2×5=10 ⇒ab−10=ad ...(i) b(a−c)=2×3=6 ⇒ab−6=bc ...(ii) cd=2×4=8 ...(iii) (i)×(ii): (ab−10)(ab−6)=abcd (ab−10)(ab−6)=8ab (ab)^2 −24(ab)+60=0 ⇒ab=12+2(√(21))=area of rectangle A_(ΔDXY) =ab−(3+4+5)=2(√(21)) generally: (ab−2A)(ab−2C)=2Bab (ab)^2 −2(A+B+C)(ab)+4AC=0 ab=A+B+C+(√((A+B+C)^2 −4AC)) A_(ΔDXY) =(√((A+B+C)^2 −4AC))

$${a}\left({b}−{d}\right)=\mathrm{2}×\mathrm{5}=\mathrm{10} \\ $$$$\Rightarrow{ab}−\mathrm{10}={ad}\:\:\:\:…\left({i}\right) \\ $$$${b}\left({a}−{c}\right)=\mathrm{2}×\mathrm{3}=\mathrm{6} \\ $$$$\Rightarrow{ab}−\mathrm{6}={bc}\:\:\:\:…\left({ii}\right) \\ $$$${cd}=\mathrm{2}×\mathrm{4}=\mathrm{8}\:\:\:…\left({iii}\right) \\ $$$$\left({i}\right)×\left({ii}\right): \\ $$$$\left({ab}−\mathrm{10}\right)\left({ab}−\mathrm{6}\right)={abcd} \\ $$$$\left({ab}−\mathrm{10}\right)\left({ab}−\mathrm{6}\right)=\mathrm{8}{ab} \\ $$$$\left({ab}\right)^{\mathrm{2}} −\mathrm{24}\left({ab}\right)+\mathrm{60}=\mathrm{0} \\ $$$$\Rightarrow{ab}=\mathrm{12}+\mathrm{2}\sqrt{\mathrm{21}}={area}\:{of}\:{rectangle} \\ $$$${A}_{\Delta{DXY}} ={ab}−\left(\mathrm{3}+\mathrm{4}+\mathrm{5}\right)=\mathrm{2}\sqrt{\mathrm{21}} \\ $$$$ \\ $$$${generally}: \\ $$$$\left({ab}−\mathrm{2}{A}\right)\left({ab}−\mathrm{2}{C}\right)=\mathrm{2}{Bab} \\ $$$$\left({ab}\right)^{\mathrm{2}} −\mathrm{2}\left({A}+{B}+{C}\right)\left({ab}\right)+\mathrm{4}{AC}=\mathrm{0} \\ $$$${ab}={A}+{B}+{C}+\sqrt{\left({A}+{B}+{C}\right)^{\mathrm{2}} −\mathrm{4}{AC}} \\ $$$${A}_{\Delta{DXY}} =\sqrt{\left({A}+{B}+{C}\right)^{\mathrm{2}} −\mathrm{4}{AC}} \\ $$

Commented by M±th+et£s last updated on 29/Feb/20

$${thank}\:{you}\:{sir} \\ $$

Facebook Tweet Pin

Leave a Reply Cancel reply