Question Number 83331 by oyemi kemewari last updated on 01/Mar/20

Commented by jagoll last updated on 01/Mar/20
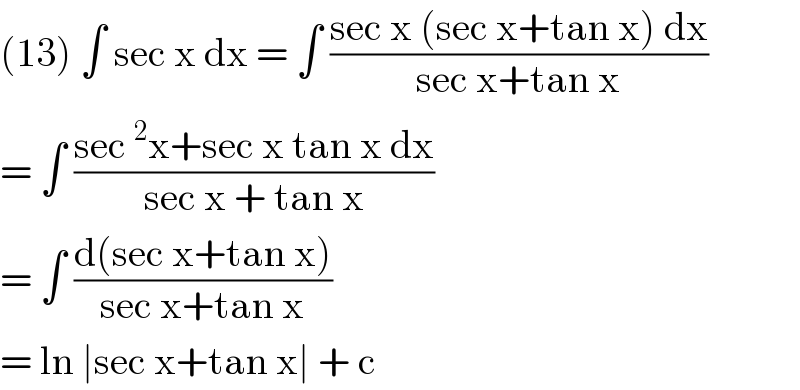
$$\left(\mathrm{13}\right)\:\int\:\mathrm{sec}\:\mathrm{x}\:\mathrm{dx}\:=\:\int\:\frac{\mathrm{sec}\:\mathrm{x}\:\left(\mathrm{sec}\:\mathrm{x}+\mathrm{tan}\:\mathrm{x}\right)\:\mathrm{dx}}{\mathrm{sec}\:\mathrm{x}+\mathrm{tan}\:\mathrm{x}} \\ $$$$=\:\int\:\frac{\mathrm{sec}\:^{\mathrm{2}} \mathrm{x}+\mathrm{sec}\:\mathrm{x}\:\mathrm{tan}\:\mathrm{x}\:\mathrm{dx}}{\mathrm{sec}\:\mathrm{x}\:+\:\mathrm{tan}\:\mathrm{x}} \\ $$$$=\:\int\:\frac{\mathrm{d}\left(\mathrm{sec}\:\mathrm{x}+\mathrm{tan}\:\mathrm{x}\right)}{\mathrm{sec}\:\mathrm{x}+\mathrm{tan}\:\mathrm{x}} \\ $$$$=\:\mathrm{ln}\:\mid\mathrm{sec}\:\mathrm{x}+\mathrm{tan}\:\mathrm{x}\mid\:+\:\mathrm{c} \\ $$
Commented by mr W last updated on 01/Mar/20
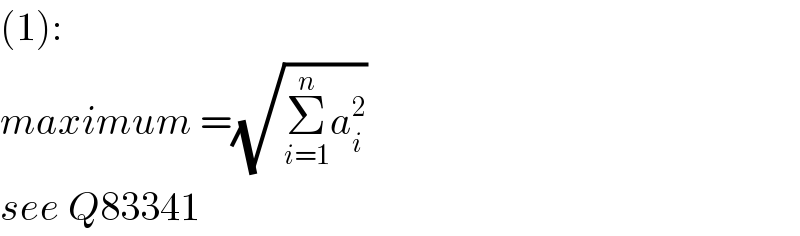
$$\left(\mathrm{1}\right): \\ $$$${maximum}\:=\sqrt{\underset{{i}=\mathrm{1}} {\overset{{n}} {\sum}}{a}_{{i}} ^{\mathrm{2}} } \\ $$$${see}\:{Q}\mathrm{83341} \\ $$
Commented by abdomathmax last updated on 01/Mar/20
![15)we use the diffeomorphism(r,θ)→(x,y) / x=rcosθ and y =rsinθ we have x,y≥0 ⇒0≤θ≤(π/2) ∫_0 ^∞ ∫_0 ^∞ e^(−(x^2 +y^2 )) dxdy =∫_0 ^∞ ∫_0 ^(π/2) e^(−r^2 ) rdrdθ =(π/2) ∫_0 ^∞ r e^(−r^2 ) dr =(π/2)[−(1/2)e^(−r^2 ) ]_0 ^(+∞) =(π/4)](https://www.tinkutara.com/question/Q83346.png)
$$\left.\mathrm{15}\right){we}\:{use}\:{the}\:{diffeomorphism}\left({r},\theta\right)\rightarrow\left({x},{y}\right)\:/ \\ $$$${x}={rcos}\theta\:{and}\:{y}\:={rsin}\theta\:\:{we}\:{have}\:{x},{y}\geqslant\mathrm{0}\:\Rightarrow\mathrm{0}\leqslant\theta\leqslant\frac{\pi}{\mathrm{2}} \\ $$$$\int_{\mathrm{0}} ^{\infty} \int_{\mathrm{0}} ^{\infty} \:{e}^{−\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right)} {dxdy}\:=\int_{\mathrm{0}} ^{\infty} \:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:{e}^{−{r}^{\mathrm{2}} } {rdrd}\theta \\ $$$$=\frac{\pi}{\mathrm{2}}\:\int_{\mathrm{0}} ^{\infty} {r}\:{e}^{−{r}^{\mathrm{2}} } {dr}\:=\frac{\pi}{\mathrm{2}}\left[−\frac{\mathrm{1}}{\mathrm{2}}{e}^{−{r}^{\mathrm{2}} } \right]_{\mathrm{0}} ^{+\infty} \:=\frac{\pi}{\mathrm{4}} \\ $$
Commented by abdomathmax last updated on 01/Mar/20
![18) A =∫_0 ^a ∫_0 ^a ((xdxdy)/( (√(x^2 +y^2 )))) (we suppose a>0) we use the diffeomorphism(r,θ)→(x,y)=(rcosθ,rsinθ) ⇒ 0≤x,y≤a ⇒ 0≤x^2 ,y^2 ≤a^2 ⇒0≤x^2 +y^2 ≤2a^2 ⇒ 0≤r^2 ≤2a^2 ⇒0≤r≤a(√2) ⇒ A=∫_0 ^(a(√2)) ∫_0 ^(π/2) ((rcosθ rdrdθ)/r) =∫_0 ^(a(√2)) rdr ∫_0 ^(π/2) dθ =(π/2)[(r^2 /2)]_0 ^(a(√2)) =(π/2)(((2a^2 )/2)) =((πa^2 )/2)](https://www.tinkutara.com/question/Q83347.png)
$$\left.\mathrm{18}\right)\:{A}\:=\int_{\mathrm{0}} ^{{a}} \int_{\mathrm{0}} ^{{a}} \:\:\frac{{xdxdy}}{\:\sqrt{{x}^{\mathrm{2}} +{y}^{\mathrm{2}} }}\:\:\:\left({we}\:{suppose}\:{a}>\mathrm{0}\right)\:{we}\:{use} \\ $$$${the}\:{diffeomorphism}\left({r},\theta\right)\rightarrow\left({x},{y}\right)=\left({rcos}\theta,{rsin}\theta\right)\:\Rightarrow \\ $$$$\mathrm{0}\leqslant{x},{y}\leqslant{a}\:\Rightarrow\:\mathrm{0}\leqslant{x}^{\mathrm{2}} ,{y}^{\mathrm{2}} \leqslant{a}^{\mathrm{2}} \:\Rightarrow\mathrm{0}\leqslant{x}^{\mathrm{2}} \:+{y}^{\mathrm{2}} \:\leqslant\mathrm{2}{a}^{\mathrm{2}} \:\Rightarrow \\ $$$$\mathrm{0}\leqslant{r}^{\mathrm{2}} \leqslant\mathrm{2}{a}^{\mathrm{2}} \:\Rightarrow\mathrm{0}\leqslant{r}\leqslant{a}\sqrt{\mathrm{2}}\:\Rightarrow \\ $$$${A}=\int_{\mathrm{0}} ^{{a}\sqrt{\mathrm{2}}} \:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\frac{{rcos}\theta\:{rdrd}\theta}{{r}} \\ $$$$=\int_{\mathrm{0}} ^{{a}\sqrt{\mathrm{2}}} {rdr}\:\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:{d}\theta\:=\frac{\pi}{\mathrm{2}}\left[\frac{{r}^{\mathrm{2}} }{\mathrm{2}}\right]_{\mathrm{0}} ^{{a}\sqrt{\mathrm{2}}} =\frac{\pi}{\mathrm{2}}\left(\frac{\mathrm{2}{a}^{\mathrm{2}} }{\mathrm{2}}\right)\:=\frac{\pi{a}^{\mathrm{2}} }{\mathrm{2}} \\ $$
Commented by mathmax by abdo last updated on 01/Mar/20
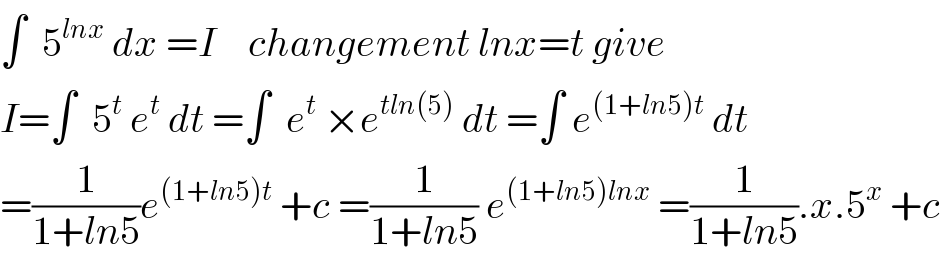
$$\int\:\:\mathrm{5}^{{lnx}} \:{dx}\:={I}\:\:\:\:{changement}\:{lnx}={t}\:{give} \\ $$$${I}=\int\:\:\mathrm{5}^{{t}} \:{e}^{{t}} \:{dt}\:=\int\:\:{e}^{{t}} \:×{e}^{{tln}\left(\mathrm{5}\right)} \:{dt}\:=\int\:{e}^{\left(\mathrm{1}+{ln}\mathrm{5}\right){t}} \:{dt} \\ $$$$=\frac{\mathrm{1}}{\mathrm{1}+{ln}\mathrm{5}}{e}^{\left(\mathrm{1}+{ln}\mathrm{5}\right){t}} \:+{c}\:=\frac{\mathrm{1}}{\mathrm{1}+{ln}\mathrm{5}}\:{e}^{\left(\mathrm{1}+{ln}\mathrm{5}\right){lnx}} \:=\frac{\mathrm{1}}{\mathrm{1}+{ln}\mathrm{5}}.{x}.\mathrm{5}^{{x}} \:+{c} \\ $$
Commented by mathmax by abdo last updated on 02/Mar/20
![23) A_n =∫_0 ^∞ ∫_0 ^∞ e^(−xy) sin(nx)dxdy =∫_0 ^∞ (∫_0 ^∞ e^(−yx ) sin(nx)dx)dy ∫_0 ^∞ e^(−yx) sin(nx) =Im(∫_0 ^∞ e^(−yx+inx) dx) ∫_0 ^∞ e^((−y+in)x) dx =[(1/(−y+in)) e^((−y+in)x) ]_0 ^(+∞) =−(1/(−y+in)) =(1/(y−in)) =((y+in)/(y^2 +n^2 )) ⇒∫_0 ^∞ e^(−yx) sin(nx)dx =(n/(y^2 +n^2 )) ⇒ A_n =n∫_0 ^∞ (dy/(y^2 +n^2 )) =_(y=nu) n∫_0 ^∞ ((ndu)/(n^2 (1+u^2 ))) =(π/2) by fubinni we have A_n =∫_0 ^∞ (∫_0 ^∞ e^(−xy) dy)sin(nx)dx =∫_0 ^∞ [−(1/x)e^(−xy) ]_(y=0) ^∞ sin(nx)dx =∫_0 ^∞ ((sin(nx))/x)dx =(π/2)](https://www.tinkutara.com/question/Q83426.png)
$$\left.\mathrm{23}\right)\:{A}_{{n}} =\int_{\mathrm{0}} ^{\infty} \int_{\mathrm{0}} ^{\infty} {e}^{−{xy}} \:{sin}\left({nx}\right){dxdy}\:=\int_{\mathrm{0}} ^{\infty} \left(\int_{\mathrm{0}} ^{\infty} \:{e}^{−{yx}\:} {sin}\left({nx}\right){dx}\right){dy} \\ $$$$\int_{\mathrm{0}} ^{\infty} \:{e}^{−{yx}} \:{sin}\left({nx}\right)\:={Im}\left(\int_{\mathrm{0}} ^{\infty} \:{e}^{−{yx}+{inx}} {dx}\right) \\ $$$$\int_{\mathrm{0}} ^{\infty} \:{e}^{\left(−{y}+{in}\right){x}} {dx}\:=\left[\frac{\mathrm{1}}{−{y}+{in}}\:{e}^{\left(−{y}+{in}\right){x}} \right]_{\mathrm{0}} ^{+\infty} =−\frac{\mathrm{1}}{−{y}+{in}}\:=\frac{\mathrm{1}}{{y}−{in}} \\ $$$$=\frac{{y}+{in}}{{y}^{\mathrm{2}} \:+{n}^{\mathrm{2}} }\:\Rightarrow\int_{\mathrm{0}} ^{\infty} \:{e}^{−{yx}} {sin}\left({nx}\right){dx}\:=\frac{{n}}{{y}^{\mathrm{2}} +{n}^{\mathrm{2}} }\:\Rightarrow \\ $$$${A}_{{n}} ={n}\int_{\mathrm{0}} ^{\infty} \:\frac{{dy}}{{y}^{\mathrm{2}} \:+{n}^{\mathrm{2}} }\:=_{{y}={nu}} \:\:\:{n}\int_{\mathrm{0}} ^{\infty} \:\:\frac{{ndu}}{{n}^{\mathrm{2}} \left(\mathrm{1}+{u}^{\mathrm{2}} \right)}\:=\frac{\pi}{\mathrm{2}}\:\:{by}\:{fubinni}\:{we}\:{have} \\ $$$${A}_{{n}} =\int_{\mathrm{0}} ^{\infty} \:\:\left(\int_{\mathrm{0}} ^{\infty} {e}^{−{xy}} {dy}\right){sin}\left({nx}\right){dx} \\ $$$$=\int_{\mathrm{0}} ^{\infty} \left[−\frac{\mathrm{1}}{{x}}{e}^{−{xy}} \right]_{{y}=\mathrm{0}} ^{\infty} \:{sin}\left({nx}\right){dx}\:=\int_{\mathrm{0}} ^{\infty} \:\frac{{sin}\left({nx}\right)}{{x}}{dx}\:=\frac{\pi}{\mathrm{2}} \\ $$$$ \\ $$
Commented by mathmax by abdo last updated on 02/Mar/20
![I =∫_0 ^∞ ((1−e^(−ax) )/x) e^(−x) dx⇒I =∫_0 ^∞ ((e^(−x) −e^(−(a+1)x) )/x)dx =ϕ(a) ϕ^′ (a) =∫_0 ^∞ e^(−(a+1)x) dx =[−(1/(a+1))e^(−(a+1)x) ]_0 ^(+∞) =(1/(a+1)) ⇒ ϕ(a) =k+ln(a+1) we have ϕ(0)=0=k ⇒ I=ln(a+1) ⇒∫_0 ^∞ ((1−e^(−x) )/x)e^(−x) dx =∫_0 ^∞ ((e^(−x) −e^(−2x) )/x)dx =ln(2)](https://www.tinkutara.com/question/Q83448.png)
$${I}\:=\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{1}−{e}^{−{ax}} }{{x}}\:{e}^{−{x}} \:{dx}\Rightarrow{I}\:=\int_{\mathrm{0}} ^{\infty} \frac{{e}^{−{x}} −{e}^{−\left({a}+\mathrm{1}\right){x}} }{{x}}{dx}\:=\varphi\left({a}\right) \\ $$$$\varphi^{'} \left({a}\right)\:=\int_{\mathrm{0}} ^{\infty} \:{e}^{−\left({a}+\mathrm{1}\right){x}} \:{dx}\:=\left[−\frac{\mathrm{1}}{{a}+\mathrm{1}}{e}^{−\left({a}+\mathrm{1}\right){x}} \right]_{\mathrm{0}} ^{+\infty} =\frac{\mathrm{1}}{{a}+\mathrm{1}}\:\Rightarrow \\ $$$$\varphi\left({a}\right)\:={k}+{ln}\left({a}+\mathrm{1}\right)\:\:{we}\:{have}\:\varphi\left(\mathrm{0}\right)=\mathrm{0}={k}\:\Rightarrow \\ $$$${I}={ln}\left({a}+\mathrm{1}\right)\:\Rightarrow\int_{\mathrm{0}} ^{\infty} \frac{\mathrm{1}−{e}^{−{x}} }{{x}}{e}^{−{x}} \:{dx}\:=\int_{\mathrm{0}} ^{\infty} \:\frac{{e}^{−{x}} −{e}^{−\mathrm{2}{x}} }{{x}}{dx}\:={ln}\left(\mathrm{2}\right) \\ $$
Answered by mind is power last updated on 02/Mar/20
![13 ) ∫_0 ^(+∞) ((1−e^(−ax) )/x)e^(−x) dx =∫_0 ^(+∞) ((e^(−x) −e^(−(a+1)x) )/x)dx=ln(((a+1)/1))=ln(a+1) ∫_0 ^(+∞) ((−Σ_(k=1) ^(+∞) (((−ax)^k e^(−x) )/(k!)))/x) =Σ_(k≥1) (−1)^(k+1) .(a^k /(k!)).∫_0 ^(+∞) x^(k−1) .e^(−x) dx =Σ_(k≥1) (((−1)^(k+1) )/(k!))a^k .Γ(k)=Σ_(k≥1) (((−1)^(k+1) )/k)a^k =ln(1+a),∀a∈]0,1[](https://www.tinkutara.com/question/Q83397.png)
$$\left.\mathrm{13}\:\right)\:\:\int_{\mathrm{0}} ^{+\infty} \frac{\mathrm{1}−{e}^{−{ax}} }{{x}}{e}^{−{x}} {dx} \\ $$$$=\int_{\mathrm{0}} ^{+\infty} \frac{{e}^{−{x}} −{e}^{−\left({a}+\mathrm{1}\right){x}} }{{x}}{dx}={ln}\left(\frac{{a}+\mathrm{1}}{\mathrm{1}}\right)={ln}\left({a}+\mathrm{1}\right) \\ $$$$\int_{\mathrm{0}} ^{+\infty} \frac{−\underset{{k}=\mathrm{1}} {\overset{+\infty} {\sum}}\frac{\left(−{ax}\right)^{{k}} {e}^{−{x}} }{{k}!}}{{x}} \\ $$$$=\underset{{k}\geqslant\mathrm{1}} {\sum}\left(−\mathrm{1}\right)^{{k}+\mathrm{1}} .\frac{{a}^{{k}} }{{k}!}.\int_{\mathrm{0}} ^{+\infty} {x}^{{k}−\mathrm{1}} .{e}^{−{x}} {dx} \\ $$$$\left.=\underset{{k}\geqslant\mathrm{1}} {\sum}\frac{\left(−\mathrm{1}\right)^{{k}+\mathrm{1}} }{{k}!}{a}^{{k}} .\Gamma\left({k}\right)=\underset{{k}\geqslant\mathrm{1}} {\sum}\frac{\left(−\mathrm{1}\right)^{{k}+\mathrm{1}} }{{k}}{a}^{{k}} ={ln}\left(\mathrm{1}+{a}\right),\forall{a}\in\right]\mathrm{0},\mathrm{1}\left[\right. \\ $$
